数据结构-经典排序算法实现及其可视化(JavaScript实现)
实现经典的9种排序算法,分析其时间复杂度以及空间复杂度,并用动画的方式演示。
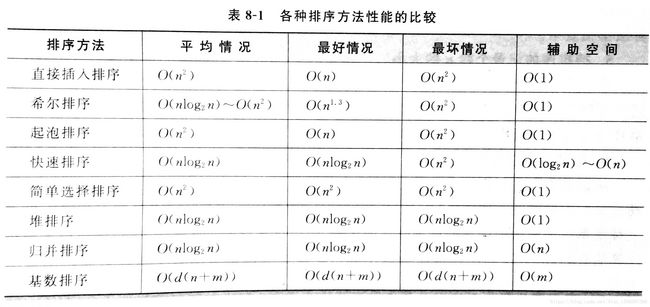
常见的算法时间复杂度由小到大依次为:
Ο(1)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n^2)<Ο(n^3)<…<Ο(2^n)<Ο(n!)
一、 直接插入排序
步骤:
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素(已排序)大于新元素,将该元素移到下一位置
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤2~5
JavaScript实现:
var insertSort = function(arr){
for(let i=1;i=0;j--){
if(arr[j] > temp){
arr[j+1] = arr[j];
arr[j] = temp;
}else{
break;//找到比temp小的则跳出循环
}
}
arr[j+1] = temp;//在比temp小的值后面插入temp值
}
return arr;
最好: O(n)
最坏: O(n^2)
平均: O(n^2)
动态图显示:
二、希尔排序
希尔排序,也叫递减增量排序,是插入排序的一种更高效的改进版本。希尔排序是不稳定的排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性
- 排序的效率但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位
JavaScript实现:
//希尔排序
var shellSort = function(arr,type,showSort){
var half = parseInt(arr.length/2);
for(let d=half;d>=1;d=parseInt(d/2) ){
for(let i=d;i=0;j-=d){
if(arr[j+d] < arr[j]){
let tem = arr[j+d];
arr[j+d] = arr[j];
arr[j] = tem;
}
}
}
}
return arr;
} 时间复杂度:
最好: O(n*log2n)
最坏: O(n^2)
三、冒泡排序
步骤:
- 比较相邻的元素,如果前一个比后一个大,就把它们两个调换位置。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
JavaScript实现:
var bubbleSort = function(arr){
for(let i=1;i arr[j+1]){
let tem = arr[j];
arr[j] = arr[j+1];
arr[j+1] = tem;
}
}
}
return arr;
} 时间复杂度:
最好: O(n)
最坏: O(n^2)
四、快速排序
步骤:
快速排序使用分治策略(Divide and Conquer)来把一个序列分为两个子序列,又称为分区交换排序。步骤为:
- 从序列中挑出一个元素,作为"轴值".
- 把所有比轴值小的元素放在轴值前面,所有比轴值大的元素放在轴值的后面,这个称为分区操作。
- 对每个分区递归地进行步骤1~2,递归的结束条件是序列的大小是0或1,这时整体已经被排好序了。
JavaScript实现:
//快速排序
var quickSort = function(arr,type,showSort){
//快速排序
var quick = function(out,first,end){
if(first时间复杂度:
最好:O(n)
平均: O(n*log2n)
最坏: O(n^2)
五、选择排序
选择排序也是一种简单直观的排序算法。它的工作原理很容易理解:初始时在序列中找到最小(大)元素,放到序列的起始位置作为已排序序列;然后,再从剩余未排序元素中继续寻找最小(大)元素,放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
注意选择排序与冒泡排序的区别:冒泡排序通过依次交换相邻两个顺序不合法的元素位置,从而将当前最小(大)元素放到合适的位置;而选择排序每遍历一次都记住了当前最小(大)元素的位置,最后仅需一次交换操作即可将其放到合适的位置。
JavaScript实现:
//选择排序
var selectSort = function(arr,type,showSort){
for(let i=0;i时间复杂度:
最好: O(n^2)
最坏: O(n^2)
六、堆排序
堆排序是指利用堆这种数据结构所设计的一种选择排序算法。堆是一种近似完全二叉树的结构(通常堆是通过一维数组来实现的),并满足性质:以最大堆(也叫大根堆、大顶堆)为例,其中父结点的值总是大于它的孩子节点。
我们可以很容易的定义堆排序的过程:
- 由输入的无序数组构造一个最大堆,作为初始的无序区
- 把堆顶元素(最大值)和堆尾元素互换
- 把堆(无序区)的尺寸缩小1,并调用heapify(A, 0)从新的堆顶元素开始进行堆调整
- 重复步骤2,直到堆的尺寸为1
JavaScript实现:
//堆排序
var heapSort = function(arr,type,showSort){
var len = arr.length;
//建立堆
var sift = function(out, k, m){
let i = k, j = 2*k+1;
while(j <= m && j!=len){
if(j out[j]){
break;
}else{
let temp = out[i];
out[i] = out[j];
out[j] = temp;
i = j;
j = 2*i+1;
}
}
}
let half = parseInt(len/2);
//初始建堆
for(let i=half-1;i>=0;i--){
sift(arr, i, len);
}
for(let i=0;i 时间复杂度:
最好: O(n*log2n)
最坏: O(n*log2n)
七、归并排序
归并排序的实现分为递归实现与非递归(迭代)实现。递归实现的归并排序是算法设计中分治策略的典型应用,我们将一个大问题分割成小问题分别解决,然后用所有小问题的答案来解决整个大问题。非递归(迭代)实现的归并排序首先进行是两两归并,然后四四归并,一直下去直到归并了整个数组。归并排序算法主要依赖归并(Merge)操作。归并操作指的是将两个已经排序的序列合并成一个序列的操作,归并操作步骤如下:
- 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
- 重复步骤3直到某一指针到达序列尾
- 将另一序列剩下的所有元素直接复制到合并序列尾
JavaScript实现:
//归并排序
var mergeSort = function(arr,type,showSort){
//一次归并算法
var merge = function(out, array, s, m, t){
let i=s, j=m+1, k=s;//i:左边数组的索引,j:右边数组的索引,k:归并结果数组的索引
//没有数组遍历完
while(i<=m && j<=t){
if(out[i] < out[j]){
array[k++] = out[i++];
}else{
array[k++] = out[j++];
}
}
//如果左数组没有遍历完,将左数组剩余数据压入arr
if(i<=m){
while(i<=m){
array[k++] = out[i++];
}
}else{
while(j<=t){
array[k++] = out[j++];
}
}
return array;
}
//一趟归并排序算法
var mergePass = function(out, array, h){
var len = out.length;
let i = 0;
while(i+2*h<=len){
merge(out, array, i , i+h-1, i+2*h-1);
i += 2*h;
}
if(i+h时间复杂度:
非递归
最好: O(n)
最坏: O(n^2)
八、桶排序
原理:
假设待排序的值都在 0~m-1 之间,设置 m 个桶(bucket),首先将值为 i 的值分配(distribute)到第 i 个桶中,然后将各个桶中的记录依次收集(collect)起来。
JavaScript实现:
//桶排序
var bucketSort = function(arr){
var distribute = function(arr){
var bucket = [];
for(let i=0;i=1){
out[index++] = i;
temp--;
}
}
return out;
}
var buckets = distribute(arr);
var out = collect(buckets);
return out;
} 时间复杂度: O(n+m)
空间复杂度: O(m)
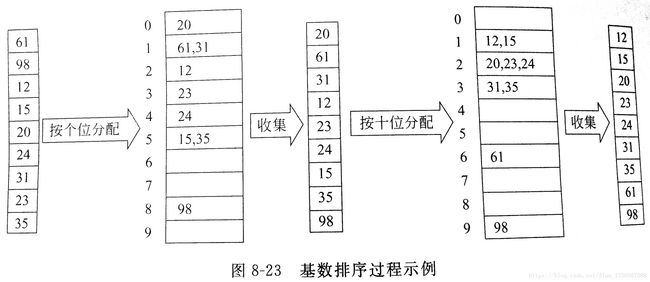
九、基数排序
基数排序是借助多关键码进行桶排序的思想进行排序。分为最主位优先 (MSD) 和最次位优先 (LSD) 。
以最次位优先为例:
JavaScript实现:
//基数排序
var radixSort = function(arr,type,showSort){
//计算所有数中最大的是几位数
var getMaxPow = function(out){
//求所有数中最大的
var max = 0;
for(let i=0;imax){
max = out[i];
}
}
//计算所有数中最大的是几位数
var max_pow = 1;
while(max>=10){
max_pow++;
max = parseInt(max/10);
}
return max_pow;
}
//升序,分配
var distribute = function(out, pow){
var queue = [];
for(let i=0;i0){
out.push(queue[i].shift());
}
}
return out;
}
var max_pow = getMaxPow(arr);
var queue = [], output = [];
for(let i=0;i 时间复杂度:
最好: O(d*(n+m)) ,其中d是最大数的位数,例如最大123,则d=3
空间复杂度: O(m)
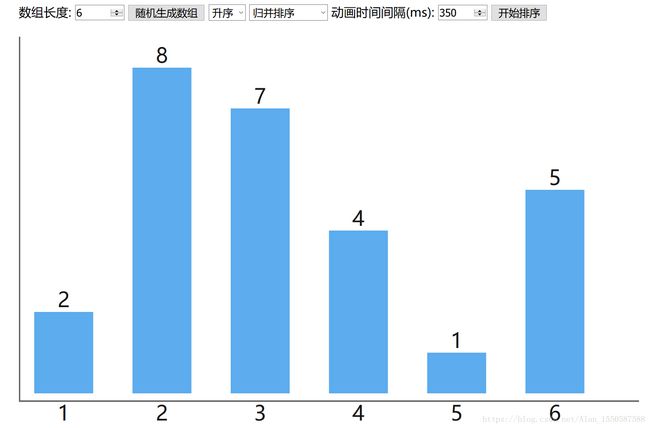
遍历可视化界面:
遍历可视化完整代码:
排序
数组长度:
动画时间间隔(ms):