SVM算法的个人笔记

一、软间隔支持向量机中惩罚参数C和 ζi ζ i

12||w||2+C∑N1ζi 1 2 | | w | | 2 + C ∑ 1 N ζ i

这里 ζi ζ i 为松弛变量， ζi≥0 ζ i ≥ 0 ，在训练数据集不是完全线性可分的情况下，通过令一些 ζi ζ i 大于0，允许其中一些样本的函数间隔小于1，特别的，当 ζi ζ i 大于1时，实际上是允许其中一些样本的函数间隔小于0，即允许算法对一些样本进行错误分类。
C为惩罚参数，当前的最小化目标函数由两项组成，包含两层含义，使 12||w||2 1 2 | | w | | 2 尽可能小，即函数间隔尽可能大；使 C∑N1ζi C ∑ 1 N ζ i 尽可能小，即错误分类点的个数尽量小，C是调节优化方向中两项（间隔大小，分类准确度）偏好的权重。即软间隔SVM针对硬间隔SVM容易出现过拟合的问题，适当放宽了间隔的大小，并容忍一些分类错误。当C趋于无穷大时，就是不允许分类误差的存在，那就是一个硬间隔SVM（过拟合）；当C趋于0时，不再关注分类是否正确，只要求间隔越大越好（欠拟合）

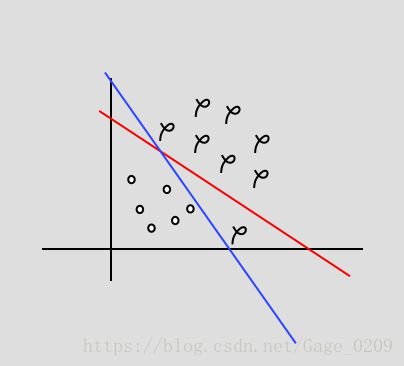
如上图所示右下角有一个异常点，蓝线为硬间隔模型的分界面（过拟合），红线为软间隔模型的分界面（允许错误分类）
二、 η η 的正负问题

η=K11+K22−2K12 η = K 11 + K 22 − 2 K 12

η η 是在求解 α2 α 2 的计算过程中解析出来的，正常情况下， η η 是大于0的，而在异常情况下， η≤0 η ≤ 0 。其中，在核函数K不满足Mercer条件（如果K是一个合法的核，那么它所对应的核矩阵是半正定矩阵，这个条件是充分必要的）的情况下， η<0 η < 0 ；而在不止一个训练样本有相同的输入向量X的情况下，即使K是合法的，也会出现 η=0 η = 0 的情况。
三、什么情况算违反KKT条件
所谓的KKT条件是指：

αi=0⇔yig(xi)≥1 α i = 0 ⇔ y i g ( x i ) ≥ 1
0<αi<C⇔yig(xi)=1 0 < α i < C ⇔ y i g ( x i ) = 1
αi=C⇔yig(xi)≤1 α i = C ⇔ y i g ( x i ) ≤ 1

所以

αi>0⇔yig(xi)≤1 α i > 0 ⇔ y i g ( x i ) ≤ 1
αi<C⇔yig(xi)≥1 α i < C ⇔ y i g ( x i ) ≥ 1

所以如果以下情况发生，就是违背了KKT条件

αi>0 α i > 0 但 yig(xi)>1 y i g ( x i ) > 1
αi<C α i < C 但 yig(xi)<1 y i g ( x i ) < 1

四、样本违背KKT条件检验是在 ε ε 精度范围内进行的。

αi>0 α i > 0 且 yig(xi)>1+ε y i g ( x i ) > 1 + ε
αi<C α i < C 且 yig(xi)<1−ε y i g ( x i ) < 1 − ε

ε ε 通常取 10−3 10 − 3 ，识别系统通常没必要让KKT条件检验满足非常高的精度，算法输出的某些训练样本正的间隔在0.999和1.001之间也是可以接受的，不算其违反KKT条件。如果要求输出的精度非常高，SMO算法的收敛速度会下降很多。
了解完算法之后就可以实战了

import numpy as np
#辅助函数
#打开文件并逐行解析，从而得到没行的类别标签和整个数据矩阵
def loadDataSet(filename):
    dataMat = []
    labelMat = []
    fr = open(filename)
    for line in fr.readlines():
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]), float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat, labelMat

#选择一个不等于i的j
def selectJrand(i,m):
    j = i 
    while(j == i):
        j = int(random.uniform(0,m))
    return j

#对alphanew、unc进行裁剪
def clipAlpha(aj, H, L):
    if aj > H:
        aj = H
    if aj < L:
        aj = L
    return aj

#简化版SMO算法
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
    dataMatrix = np.mat(dataMatIn)
    labelMat = np.mat(classLabels).transpose()
    m,n = np.shape(dataMatrix)
    #初始化alpha向量和截距b
    b = 0
    alphas = np.mat(zeros((m,1)))
    iter = 0
    #外循环
    while(iter < maxIter):
        alphaPairsChanged = 0
        #内循环
        for i in range(m):
            #预测的类别
            fXi = float(np.multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[i,:].T)) + b 
            #误差：预测值与真实输出之差
            Ei = fXi - float(labelMat[i])
            #在toler范围内检验样本i是否违背KKT条件
            if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
                #如果i违背了KKT条件，说明alpha_i是可以被优化的，随机选择另一个数据向量j，同时优化这两个向量
                j = selectJrand(i, m)
                fXj = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[j,:].T)) + b
                Ej = fXj - float(labelMat[j])
                alphaIold = alphas[i].copy()
                alphaJold = alphas[j].copy()
                if (labelMat[i] != labelMat[j]):
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] - alphas[i] - C)
                    H = min(C, alphas[j] - alphas[i])
                if L == H: print "L == H"; continue
                eta = dataMatrix[i,:] * dataMatrix[i,:].T + dataMatrix[j,:] * dataMatrix[j,:].T - 2.0 * dataMatrix[i,:] * dataMatrix[j,:].T
                if eta <= 0: print "eta <= 0"; continue
                alphas[j] += labelMat[j] * (Ei - Ej)/eta
                #根据不等式约束将其限制在区间[L,H]内
                alphas[j] = clipAlpha(alphas[j], H, L)
                #检查alpha_j是否有轻微改变
                if (abs(alphas[j] - alphaJold) < 0.00001): 
                    print "j not moving enough"
                    continue
                alphas[i] += labelMat[j] * labelMat[i] * (alphaJold - alphas[j])
                b1 = b - Ei - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i,:] * dataMatrix[i,:].T - labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[j,:] * dataMatrix[i,:].T
                b2 = b - Ej - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i,:] * dataMatrix[j,:].T  - labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[j,:] * dataMatrix[j,:].T
                if (0 < alphas[i]) and (C > alphas[i]): b = b1
                elif (0 < alphas[j]) and (C > alphas[j]): b = b2
                else: b = (b1 + b2) / 2.0
                #执行到for循环的最后一行都不执行continue语句，说明成功的改变了一对alpha
                alphaPairsChanged += 1
                print "iter: %d i: %d, pairs changed %d" %(iter, i, alphaPairsChanged)
        #如果所有向量都没被优化，增加迭代数目，继续下一次循环
        #只有在所有数据集上遍历maxIter次，且不再发生任何alpha修改之后，程序才会停止并退出while循环
        if (alphaPairsChanged == 0):
            iter += 1
        #如果alpha有更新，将iter归零继续运行程序
        else:
            iter = 0
        print "iteration number: %d" % iter 
    return b, alphas

以上算法就计算出了alpha向量和b，据此可以求出w，以对新输入进行预测
w∗=∑Ni=1α∗iyixi w ∗ = ∑ i = 1 N α i ∗ y i x i

#基于alpha值得到超平面，包括w的计算
def calcWs(alphas, dataArr, classLabels):
    X = mat(dataArr)
    labelMat = mat(labelArr).transpose()
    m,n = shape(X)
    w = zeros((n,1))
    for i in range(m):
        w += multiply(alphas[i]*labelMat[i], X[i,:].T)
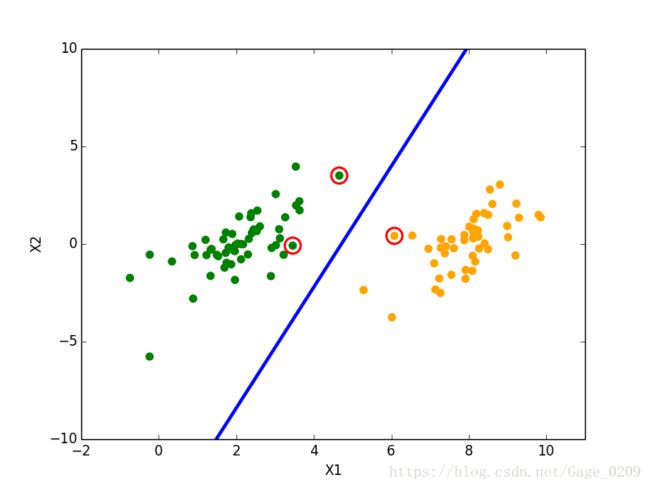
    return w 

有了w和b就可以绘制出超平面（w,b），绘制超平面和训练样本散点图程序如下所示：

b, alphas = svmMLiA.smoSimple(dataArr, labelArr, 0.6, 0.001, 40)
w = calcWs(alphas, dataArr, labelArr)
#斜率和截距
k = -float(w[0]/w[1])
b_new = -float(b/w[1])
#绘制超平面（w,b）需要的数据
x = np.linspace(-2,11)
y = k*x + b_new
#两类数据
type1 = []
type2 = []
for i in range(len(dataArr)):
    if labelArr[i] > 0:
        type1.append(dataArr[i])
    else:
        type2.append(dataArr[i])
#找出支持向量
supportVec = []
for i in range(100):
    if alphas[i] > 0.0:
        supportVec.append(dataArr[i])

import matplotlib.pyplot as plt

plt.figure()
plt.ylim(-10,10)
plt.xlim(-2,11)
plt.scatter(np.transpose(type1)[0], np.transpose(type1)[1], s = 40, color = 'orange')
plt.scatter(np.transpose(type2)[0], np.transpose(type2)[1], s = 40, color = 'green')
plt.plot(x,y, color = 'blue', linewidth = 3.0)
plt.scatter(np.transpose(supportVec)[0], np.transpose(supportVec)[1], s = 200, color = '', edgecolor = 'red', linewidth = 2.0)
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()

结果如下图所示：

其中中间加粗的蓝线为分隔超平面，用红色的圆圈圈出来的是支持向量（到分隔超平面的距离最近（为1）的点）