浪在ACM10.26第二次训练赛

 

A.海港

题目描述

 

输入

 

输出

输出n行，第i行输出一个整数表示第i艘船到达后的统计信息。

 

样例输入

3
1 4 4 1 2 2
2 2 2 3
10 1 3

 

样例输出

3
4
4

 

提示

【样例解释1】 

第一艘船在第1秒到达海港，最近24小时到达的船是第一艘船，共有4个乘客， 分别是来自国家4,1,2,2共来自3个不同的国家； 

第二艘船在第2秒到达海港，最近24小时到达的船是第一艘船和第二艘船，共有4 + 2 =6个乘客，分别是来自国家4,1,2,2,2,3共来自4个不同的国家； 

第三艘船在第10秒到达海港，最近24小时到达的船是第一艘船、第二艘船和第 三艘船，共有4+ 2+1=7个乘客，分别是来自国家4,1,2,2,2,3,3共来自4个不同 的国家。 

 

这个题，一上来手写队列，不过好像写挫了(ಥ _ ಥ)，后来又用的STL里的queue队列。为啥用队列呢，因为输入是按时间升序，所以先入者先出，然后就用队列惹...

思路是每输入一个时间国家就push一下，这里注意因为一个时间可能对应多个国家，所以要push国家的个数p个，对应的国家数加1，如果这个国家唯一的话，sum++记录一下。当时间差>86400时，pop，当时间差<=86400时，对应的国家数减1，当这个国家数等于0时，sum--,然后pop。

#include
using namespace std;
int x[100001],n,sum;
struct node
{
    int t,g;
};
queue  h;

int main()
{
    scanf("%d",&n);
    for(int i=0;i

 

C.金币

题目描述

国王将金币作为工资，发放给忠诚的骑士。第一天，骑士收到一枚金币；之后两天（第二天和第三天），每天收到两枚金币；之后三天（第四、五、六天），每天收到三枚金币；之后四天（第七、八、九、十天），每天收到四枚金币……；这种工资发放模式会一直这样延续下去：当连续N天每天收到N枚金币后，骑士会在之后的连续N+1N+1天里，每天收到N+1N+1枚金币。

请计算在前KK天里，骑士一共获得了多少金币。

输入输出格式

输入格式：

 

一个正整数KK，表示发放金币的天数。

 

输出格式：

 

一个正整数，即骑士收到的金币数。

 

输入输出样例

输入样例#1： 

6

输出样例#1： 

14

输入样例#2： 

1000

输出样例#2： 

29820

说明

【输入输出样例 1 说明】

骑士第一天收到一枚金币；第二天和第三天，每天收到两枚金币；第四、五、六天，每天收到三枚金币。因此一共收到 1+2+2+3+3+3=141+2+2+3+3+3=14 枚金币。

对于 100\%100%的数据，1 ≤ K ≤ 10,0001≤K≤10,000。

 

1  2, 2  3,3,3   4,4,4,4     每一个数i的和是 i*i

举个栗子 6天的话 1 2,2  3,3,3 金币     1+2+3天

7天的话  1  2,2  3,3,3   4,4,4,4   其中4天多了3个 此时 h=1+2+3+4  h-n=3 多了3天 

也就是金币多出来的是(h-n)*i，ans减去就好了。  

#include
using namespace std;
int n;
long long ans=0;
int main()
{
    cin>>n;
    int h=0;     //天数
    for(int i=1;;i++)
    {
        ans+=i*i;//增加
        h+=i;
        if(h>n)         //如果加过了
        {               
            ans-=(h-n)*i;//减去多余的
            h=n;
        }
        if(h==n)break;
    }
    cout<

 

D.回文日期

题目描述

在日常生活中，通过年、月、日这三个要素可以表示出一个唯一确定的日期。

牛牛习惯用88位数字表示一个日期，其中，前44位代表年份，接下来22位代表月 份，最后22位代表日期。显然：一个日期只有一种表示方法，而两个不同的日期的表 示方法不会相同。

牛牛认为，一个日期是回文的，当且仅当表示这个日期的8位数字是回文的。现 在，牛牛想知道：在他指定的两个日期之间包含这两个日期本身），有多少个真实存 在的日期是回文的。

一个88位数字是回文的，当且仅当对于所有的i ( 1 \le i \le 8)i(1≤i≤8)从左向右数的第i个 数字和第9-i9−i个数字（即从右向左数的第ii个数字）是相同的。

例如：

•对于2016年11月19日，用88位数字2016111920161119表示，它不是回文的。

•对于2010年1月2日，用88位数字2010010220100102表示，它是回文的。

•对于2010年10月2日，用88位数字2010100220101002表示，它不是回文的。

每一年中都有1212个月份：

其中，1,3,5,7,8,10,121,3,5,7,8,10,12月每个月有3131天；4,6,9,114,6,9,11月每个月有3030天；而对于22月，闰年时有2929天，平年时有2828天。

一个年份是闰年当且仅当它满足下列两种情况其中的一种：

1.这个年份是44的整数倍，但不是100100的整数倍；

2.这个年份是400400的整数倍。

例如：

•以下几个年份都是闰年：2000,2012,20162000,2012,2016。

•以下几个年份是平年：1900,2011,20141900,2011,2014。

输入输出格式

输入格式：

 

两行，每行包括一个88位数字。

第一行表示牛牛指定的起始日期。

第二行表示牛牛指定的终止日期。

保证date\_idate_i和都是真实存在的日期，且年份部分一定为44位数字，且首位数字不为00。

保证date 1date1 —定不晚于date 2date2。

 

输出格式：

 

一个整数，表示在date1date1和date2date2之间，有多少个日期是回文的。

 

输入输出样例

输入样例#1： 

20110101

20111231

输出样例#1： 

1

输入样例#2： 

20000101
20101231

输出样例#2： 

2

说明

【样例说明】

对于样例1，符合条件的日期是20111102。

对于样例2，符合条件的日期是2001100220011002和20100102。

【子任务】

对于60\%60%的数据，满足date1 = date2date1=date2。

 

 

因为是回文，所以后四位枚举然后构成对应的回文日期，看是否在输入的范围内。

需要注意的是 闰年2月29天 那么就是0229，只有9220 0229才是回文，恰好9220是闰年。所以就阔以把2月当29天来看了。

#include
using namespace std;
int n,m,flag,sum,Count;
int s[13]={0,31,29,31,30,31,30,31,31,30,31,30,31};
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=12;i++)     //枚举月和日
    {
        for(int j=1;j<=s[i];j++)
        {
            flag=(j%10)*1000+
              (j/10)*100+
              (i%10)*10+
              (i/10);//算出前四位。
            sum=flag*10000+i*100+j; //对应的回文日期
            if (summ) //如果这个日期不在范围内
                continue;
            Count++;
        }
    }

    printf("%d",Count);
    return 0;
}

E.求和

 

题目描述

一条狭长的纸带被均匀划分出了n个格子，格子编号从1到n。每个格子上都染了一种颜色color_i用[1,m]当中的一个整数表示，并且写了一个数字number_i。 

定义一种特殊的三元组:(x,y,z)，其中x,y,z 都代表纸带上格子的编号，这里的三元组要求满足以下两个条件： 

1. xyz是整数,x
2. colorx=colorz 

满足上述条件的三元组的分数规定为(x+z) *(number_x+number_z)。整个纸带的分数规定为所有满足条件的三元组的分数的和。这个分数可能会很大，你只要输出整个纸带的分数除以10,007所得的余数即可。 
 

 

输入

第一行是用一个空格隔开的两个正整数n和m,n表纸带上格子的个数，m表纸带上颜色的种类数。 第二行有n用空格隔开的正整数，第i数字number表纸带上编号为i格子上面写的数字。 第三行有n用空格隔开的正整数，第i数字color表纸带上编号为ii格子染的颜色。

 

输出

共一行，一个整数，表示所求的纸带分数除以 10,007 所得的余数。 

 

样例输入

6 2 
5 5 3 2 2 2 
2 2 1 1 2 1 

 

样例输出

82

 

提示

【输入输出样例 说明】   
纸带如题目描述中的图所示。   
所有满足条件的三元组为：(1,3,5),(4,5,6)。   
所以纸带的分数为(1+5)∗(5+2)+(4+6)∗(2+2) = 42+40 = 82。  


【数据说明】  
对于第 1 组至第 2 组数据， 1 ≤ n ≤ 100, 1 ≤ m ≤ 5, 

对于第3 组至第 4 组数据， 1 ≤ n ≤ 3000, 1 ≤ m ≤ 100 

对于第 5 组至第6组数据， 1 ≤ n ≤ 100000, 1 ≤ m ≤ 100000且不存在出现次数超过20的颜色； 

对 于 全 部 10 组 数 据 ， 1 ≤ n ≤ 100000, 1 ≤ m ≤ 100000,1≤color_i≤m,1≤number_i≤100000 

 

这个题一开始也想到了分组求，但是通项公式没推出来(默默地说一声，数学好啊 擦一把泪 (ಥ _ ಥ)嘤嘤嘤)

后来看了洛谷上大佬的公式%%%，然后又滚去推，终于 推出来了(流下了不学无术的眼泪)。

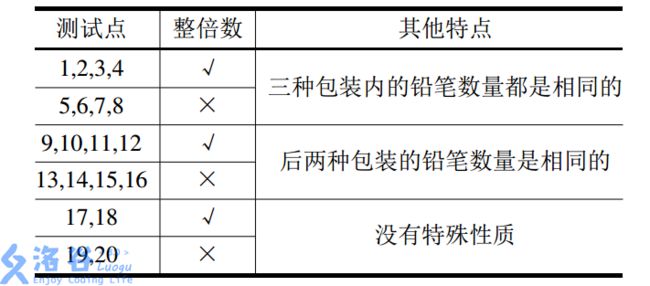
这种三元组有两个条件 1.x

三元组的分数是(x+z) *(number_x+number_z)，设n1,n2,n3,n4...nx.是颜色相同奇偶性相同的数(分为一组)，m1,m2,m3,m4...mx分别是格子上的数 (x是组里的数的个数)

首先看n1和其他的ni组成的三元组的和（n1+n2)*(m1+m2)+(n1+n3)*(m1+m3)+(n1+n4)*(m1+m4)+....+(n1+nx)*(m1+mx)=

(n1*m1+n1*m2)+(n1*m1+n1*m3)+...(n1*m1+n1*mx)=n1*(m1+m2+m3+...+mx)+(x-2)*n1*m1;同理n1和其他的ni组成的三元组的和n2*(m1+m2+m3+...+mx)+(x-2)*n2*m2，我们就可以得出每一个ni组成的三元组的和等于 ni*(m1+m2+m3+...+mx)+(x-2)*ni),那么

总和就是（n1+n2+n3+...+nx)*(m1+m2+m3+...mx)+(x-2)*(n1*m1+n2*m2+n3*m3+...+nx*mx),我们可以把x在输入的时候记录一下，输入一个颜色相同奇偶性相同的数就+1，同理，我们也可以用sum记录一下m1+m2+...mx，这样我们所退=推出来公式就又可以简化一下了颜色相同奇偶性相同的数的个数 (cnum-2) *Σ(i*number_i)  + Σi * sum 也就是

Σi *（(cnum-2)*Σnumber_i+sum）  记得mod10007

#include
using namespace std;
int a[100005],col[100005];
int cnum[100005][2],sum[100005][2];
int n,m,ans=0;
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
    }
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&col[i]);
        cnum[col[i]][i%2]++;   //按颜色和奇偶数分组,符合要求就+1
        sum[col[i]][i%2]=(sum[col[i]][i%2]+a[i])%10007;   //组内number_i求和
    }
    long long ans2=0;
    for(int i=1;i<=n;i++)
    {
        ans=(ans+i*((cnum[col[i]][i%2]-2)*a[i]%10007+sum[col[i]][i%2]))%10007;
    }
    cout<

 

F.推销员

题目描述

阿明是一名推销员，他奉命到螺丝街推销他们公司的产品。螺丝街是一条死胡同，出口 与入口是同一个，街道的一侧是围墙，另一侧是住户。螺丝街一共有 N 家住户，第 i 家住户 到入口的距离为 Si 米。由于同一栋房子里可以有多家住户，所以可能有多家住户与入口的 距离相等。阿明会从入口进入，依次向螺丝街的 X 家住户推销产品，然后再原路走出去。   阿明每走 1 米就会积累 1 点疲劳值，向第 i 家住户推销产品会积累 Ai点疲劳值。阿明 是工作狂，他想知道，对于不同的 X，在不走多余的路的前提下，他最多可以积累多少点疲 劳值.

 

输入

第一行有一个正整数 N，表示螺丝街住户的数量。    接下来的一行有 N 个正整数，其中第 i 个整数 Si表示第 i 家住户到入口的距离。数据保 证 S1≤S2≤…≤Sn<1e8。    接下来的一行有 N 个正整数，其中第 i 个整数 Ai表示向第 i 户住户推销产品会积累的 疲劳值。数据保证 Ai<1e3。 

 

输出

输出 N 行，每行一个正整数，第 i 行整数表示当 X=i 时，阿明最多积累的疲劳值。 

 

样例输入

5  
1 2 3 4 5  
1 2 3 4 5

 

样例输出

15  
19  
22 
24 
25

 

提示

【输入输出样例  说明】  
X=1: 向住户 5 推销，往返走路的疲劳值为 5+5，推销的疲劳值为 5，总疲劳值为 15。    
X=2: 向住户 4、5 推销，往返走路的疲劳值为 5+5，推销的疲劳值为 4+5，总疲劳 值为 5+5+4+5=19。  
X=3: 向住户 3、4、5 推销，往返走路的疲劳值为 5+5，推销的疲劳值 3+4+5，总疲 劳值为 5+5+3+4+5=22。   
X=4: 向住户 2、3、4、5 推销，往返走路的疲劳值为 5+5，推销的疲劳值 2+3+4+5， 总疲劳值 5+5+2+3+4+5=24。   
X=5: 向住户 1、 2、 3、 4、 5 推销，往返走路的疲劳值为 5+5，推销的疲劳值 1+2+3+4+5， 总疲劳值 5+5+1+2+3+4+5=25。  

 

贪心做法（然鹅自己也不会贪(╥╯^╰╥）），我们需要做的就是把X最大化，那么怎样才能最大呢，就是找前i个最大的 价值之和+两倍的最大距离(价值就是指拜访所花体力)，我们可以把价值从大到小排序，然后求一下前i个价值的前缀和sum，再把距离s根据价值的顺序从大到小排序,q[i]表示前i个数的距离最大值，能选到的最远距离，sum[i]+2*q[i]这样就可能是最大的了，为什么说可能呢，因为还有一种情况米有考虑，就是可能拜访这个住宅的所花的体力不是很大的，氮素，它距离远啊（体力花在路上了 ㄟ( ▔, ▔ )ㄏ）。这种情况就可以用前i-1个价值的最大值+（这个住宅的价值+2*这个住宅的距离），由于这种情况的存在，我们就另开一个数组h来存一下后i个数的 价值+2*距离，这种情况也就是sum[i-1]+h[i]。

所以最大的X=max(sum[i-1]+h[i],sum[i]+2*q[i]),    ok,完美结束（小花花送给寄几(✿◕‿◕✿)）

 

#include
#include
#include
using namespace std;
struct home
{
	int s,v;
	bool operator < (const home &h) const
	{
	    return h.v=1; i--) // 从后i个数的最大值。
		h[i]=max(h[i+1],2*a[i].s+a[i].v);

	for (int i=1; i<=n; i++)
    {
		printf("%d\n",max(sum[i-1]+h[i],sum[i]+2*q[i]));
	}
}

 

 

 

G.扫雷游戏

题目描述

扫雷游戏是一款十分经典的单机小游戏。在nn行mm列的雷区中有一些格子含有地雷（称之为地雷格），其他格子不含地雷（称之为非地雷格）。玩家翻开一个非地雷格时，该格将会出现一个数字——提示周围格子中有多少个是地雷格。游戏的目标是在不翻出任何地雷格的条件下，找出所有的非地雷格。

现在给出nn行mm列的雷区中的地雷分布，要求计算出每个非地雷格周围的地雷格数。

注：一个格子的周围格子包括其上、下、左、右、左上、右上、左下、右下八个方向上与之直接相邻的格子。

输入输出格式

输入格式：

 

第一行是用一个空格隔开的两个整数nn和mm，分别表示雷区的行数和列数。

接下来nn行，每行mm个字符，描述了雷区中的地雷分布情况。字符’*’表示相应格子是地雷格，字符’?’表示相应格子是非地雷格。相邻字符之间无分隔符。

 

输出格式：

 

输出文件包含nn行，每行mm个字符，描述整个雷区。用’*’表示地雷格，用周围的地雷个数表示非地雷格。相邻字符之间无分隔符。

 

输入输出样例

输入样例#1： 

3 3
*??
???
?*?

输出样例#1： 

*10
221
1*1

输入样例#2： 

2 3
?*?
*??

输出样例#2： 

2*1
*21

说明

对于 100\%100%的数据， 1≤n≤100, 1≤m≤1001≤n≤100,1≤m≤100。

 

dfs一下就好了

#include
using namespace std;
int a[8][2]={{0,-1},{0,1},{-1,0},{1,0},{-1,-1},{-1,1},{1,-1},{1,1}};
int n,m;
char Map[105][105];

void dfs(int i,int j)
{
    for(int k=0;k<8;k++)
    {
        int x=i+a[k][0];
        int y=j+a[k][1];
        if(Map[x][y]=='*')
            Map[i][j]++;
    }
}

int main()
{
    cin>>n>>m;
	for(int i=0;i>Map[i];
	for(int i=0;i

 

 

 

H.买铅笔

题目描述

P老师需要去商店买n支铅笔作为小朋友们参加NOIP的礼物。她发现商店一共有 33种包装的铅笔，不同包装内的铅笔数量有可能不同，价格也有可能不同。为了公平起 见，P老师决定只买同一种包装的铅笔。

商店不允许将铅笔的包装拆开，因此P老师可能需要购买超过nn支铅笔才够给小朋 友们发礼物。

现在P老师想知道，在商店每种包装的数量都足够的情况下，要买够至少nn支铅笔最少需要花费多少钱。

输入输出格式

输入格式：

 

第一行包含一个正整数nn，表示需要的铅笔数量。

接下来三行，每行用22个正整数描述一种包装的铅笔：其中第11个整数表示这种 包装内铅笔的数量，第22个整数表示这种包装的价格。

保证所有的77个数都是不超过1000010000的正整数。

 

输出格式：

 

11个整数，表示P老师最少需要花费的钱。

 

输入输出样例

输入样例#1： 

57
2 2
50 30
30 27

输出样例#1： 

54

输入样例#2： 

9998
128 233
128 2333
128 666

输出样例#2： 

18407

输入样例#3： 

9999
101 1111
1 9999
1111 9999

输出样例#3： 

89991

说明

铅笔的三种包装分别是：

• 22支装，价格为22;
• 5050支装，价格为3030;
• 3030支装，价格为2727。

P老师需要购买至少5757支铅笔。

如果她选择购买第一种包装，那么她需要购买2929份，共计2 \times 29 = 582×29=58支，需要花费的钱为2 \times 29 = 582×29=58。

实际上，P老师会选择购买第三种包装，这样需要买22份。虽然最后买到的铅笔数 量更多了，为30 \times 2 = 6030×2=60支，但花费却减少为27 \times 2 = 5427×2=54，比第一种少。

对于第二种包装，虽然每支铅笔的价格是最低的，但要够发必须买22份，实际的花费达到了 30 \times 2 = 6030×2=60，因此P老师也不会选择。

所以最后输出的答案是5454。

【子任务】

子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难，可以尝试 只解决一部分测试数据。

每个测试点的数据规模及特点如下表：

上表中“整倍数”的意义为：若为KK，表示对应数据所需要的铅笔数量nn—定是每种包装铅笔数量的整倍数（这意味着一定可以不用多买铅笔)。

 

 

第一眼背包哇！！有没有，然鹅，找最小值就阔以了！根本就用不到背包

注意一点，一包铅笔不能拆开

#include
using namespace std;
int dp[10005];
int c[5],v[5];
int main()
{
    int n;
    cin>>n;
    int Min=1<<30;
    for(int i=0;i<3;i++)
    {
        cin>>c[i]>>v[i];
        Min=min(Min,n%c[i]?((n/c[i]+1)*v[i]):(n/c[i])*v[i]);
    }
    cout<