Java 经典算法分析总汇
前言
在计算机软件专业中,算法分析与设计是一门非常重要的课程,很多人为它如痴如醉。很多问题的解决,程序的编写都要依赖它,在软件还是面向过程的阶段,就有‘程序=算法+数据结构’这个公式。算法的学习对于培养一个人的逻辑思维能力是有极大帮助的,它可以培养 我们养成思考分析问题,解决问题的能力。 如果一个算法有缺陷,或不适合某个问题,执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂性和时间复杂度来衡量。算法可以使用自然语言、伪代码、流程图等多种不同的方法来描述。计算机系统中的操作系统、语言编译系统、数据库管理系统以及各种各样的计算机应用系统中的软件,都必须使用具体的算法来实现。算法设计与分析是计算机科学与技术的一个核心问题。因此,学习算法无疑会增强自己的竞争力,提高自己的修为,为自己增彩。
算法概念:
算法简单来说就是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,也就是说算法告诉计算机怎么做,以此来解决问题。同一个问题存在多种算法来解决它,但是这些算法存在着优劣之分,好的算法速度快,效率高,占用空间小,差的算法不仅复杂难懂,而且效率低,对机器要求还高,当然,有时候算法之间存在一种互补关系,有些算法效率高,节省时间,但浪费空间,另外一些算法可能速度上慢些,但是空间比较节约,这时候 我们就应该根据实际要求,和具体情况来采取相应的算法来解决问题。
一、约瑟夫算法
约瑟夫环:已知n个人(以编号1,2,3...n分别表示)围坐在一张圆桌周围。从编号为k的人开始报数,数到m的那个人出列;他的下一个人又从1开始报数,数到m的那个人又出列;依此规律重复下去,直到圆桌周围的人全部出列。
- public class YuesefuTest {
- public static void main(String[] args) {
- int totalNum = 10;
- int countNum = 3;
- yuesefuByMyself(totalNum, countNum);
- yuesefu(totalNum, countNum);
- }
- /**
- * 此方法 k 为 list 的下标
- * @param totalNum
- * @param countNum
- */
- public static void yuesefuByMyself( int totalNum,int countNum){
- // 初始化人数
- List
start = new ArrayList (); - for(int i=1; i<=totalNum; i++){
- start.add(i);
- }
- // 此处的k为list的下标,开始报数人的下标,第一个人为0,第n个人为n-1
- int k = 0;
- while(start.size()>0){
- // 下一个出列人的下标,因为是从当前报数人开始数,所以减1为下一个出列人的下标
- k = k + countNum -1;
- // 当 下标+1 超过了 list 的size
- if(k + 1>start.size()){
- // 当size 为 10 ,下标要取 10 ,最大下标为9,应该取 list 的 第一个,即下标为0,
- // 同理,直接取余即可为正确下标
- k = k % start.size();
- }
- System.out.print(start.get(k)+",");
- // 出列,下一个开始报数人的下标即为出列人的下标
- start.remove(k);
- }
- System.out.println();
- }
- public static void yuesefu(int totalNum,int countNum){
- // 初始化人数
- List
start = new ArrayList (); - for(int i=1; i<=totalNum; i++){
- start.add(i);
- }
- // 从第K个开始计数
- int k = 0;
- while(start.size()>0){
- k = k + countNum;
- // 第m人的索引位置
- k = k % (start.size()) -1;
- // 判断是否到队尾
- if(k<0){
- System.out.print(start.get(start.size()-1)+",");
- start.remove(start.size()-1);
- k = 0;
- } else {
- System.out.print(start.get(k)+",");
- start.remove(k);
- }
- }
- System.out.println();
- }
- }
二、二叉树的构建及遍历
public class BinaryTree {
private static String [] array = {"A","B","D","H","","","I","","","E","","J","","",
"C","F","","K","","","G","",""};
private static int arrayIndex = 0;
// 创建一棵二叉树,约定用户遵照前序遍历的方式输入数据
// 不使用迭代是因为迭代必须要知道这棵树有多深,
// 递归只需要输入就可以自行决定深度
// type:结点类型 0 根节点 1左孩子 2右孩子
public static TreeNode createBinaryTree(int type,String parentData) {
switch (type) {
case 0:
System.out.print("根节点:");
break;
case 1:
System.out.print(parentData+"的左孩子:");
break;
case 2:
System.out.print(parentData+"的右孩子:");
break;
}
// 可以使用手动输入也可以放到数组里
// Scanner sc = new Scanner(System.in);
// String data = sc.nextLine();
String data = "";
if(arrayIndex三、线索二叉树(中序)
代码所示为下图二叉树
中序遍历:CBDAEF
C,D,F有两个空指针域,E有一个
步骤如下:
1.创建二叉树
2.创建头结点
3.中序遍历线索化
4.中序遍历此线索二叉树(非递归方式)
public class ThreadedBinaryTree {
private static String [] array = {"A","B","C","","","D","","","E","","F","",""};
private static int arrayIndex = 0;
/**
* 全局node,始终指向刚刚访问过的结点
*/
private static ThreadedBinaryNode preNode;
/**
* 1.参考创建二叉树,前序遍历输入
*/
public static ThreadedBinaryNode createThreadedBinaryTree(){
String data = "";
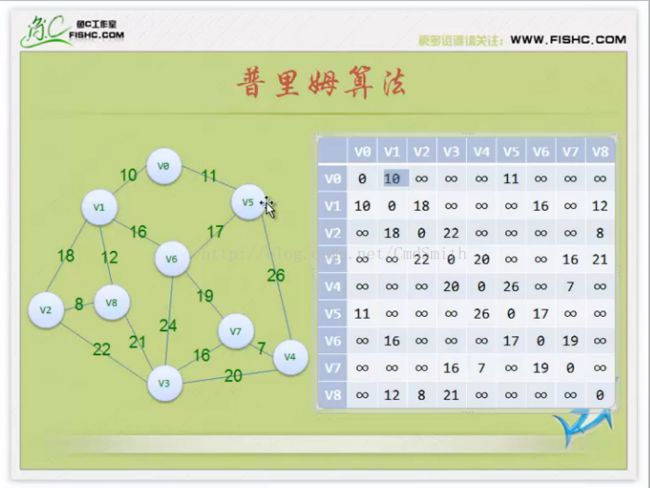
if(arrayIndex四、普里姆(Prim)算法
个人认为此算法遍历顺序的决定条件:
1.确定第一个顶点
2.下一个顶点可到(小于正无穷)
3.取可到顶点中最小权值的一个
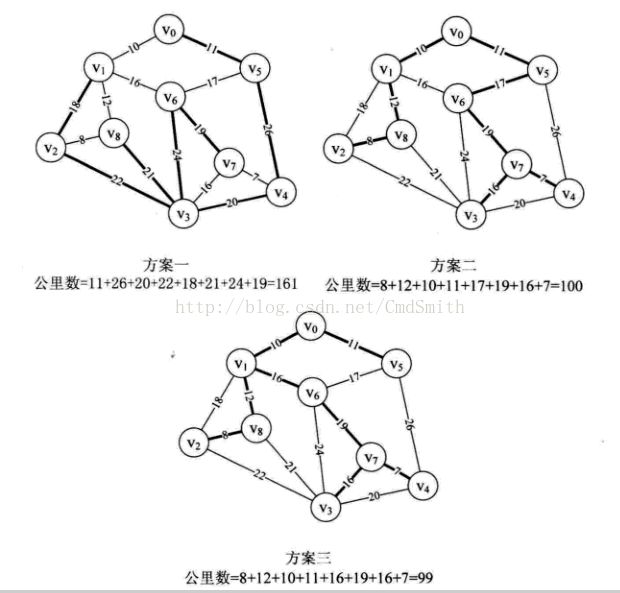
代码中的图
最小生成树:99
代码(参考其他文章):
public class MinSpanTree {
/** 邻接矩阵*/
int[][] matrix;
/** 表示正无穷*/
int MAX_WEIGHT = Integer.MAX_VALUE;
/** 顶点个数*/
int size;
/**
* 普里姆算法实现最小生成树:先初始化拿到第一个顶点相关联的权值元素放到数组中-》找到其中权值最小的顶点下标-》再根据该下标,将该下标顶点相关联的权值加入到数组中-》循环遍历处理
*/
public void prim() {
/**存放当前到全部顶点最小权值的数组,如果已经遍历过的顶点权值为0,无法到达的为正无穷*/
int[] tempWeight = new int[size];
/**当前到下一个最小权值顶点的最小权值*/
int minWeight;
/**当前到下一个最小权值的顶点*/
int minId;
/**权值总和*/
int sum = 0;
//第一个顶点时,到其他顶点的权值即为邻接矩阵的第一行
for (int i = 0; i < size; i++) {
tempWeight[i] = matrix[0][i];
}
System.out.println("从顶点v0开始查找");
for (int i = 1; i < size; i++) {
// 每次循环找出当前到下一个最小权值的顶点极其最小权值
minWeight = MAX_WEIGHT;
minId = 0;
for (int j = 1; j < size; j++) {
//权值为0的顶点已经遍历过,不再计入
if (tempWeight[j] > 0 && tempWeight[j] < minWeight) {
minWeight = tempWeight[j];
minId = j;
}
}
// 找到目标顶点minId,他的权值为minweight。
System.out.println("找到顶点:v" + minId + " 权值为:" + minWeight);
sum += minWeight;
// 算法核心所在:将目标顶点到各个顶点的权值与当前tempWeight数组中的权值做比较,如果前者比后者到某个顶点的权值更小,将前者到这个顶点的权值更新入后者。
tempWeight[minId] = 0;
for (int j = 1; j < size; j++) {
if (tempWeight[j] != 0 && matrix[minId][j] < tempWeight[j]) {
tempWeight[j] = matrix[minId][j];
}
}
}
System.out.println("最小权值总和为:" + sum);
}
private void createGraph(int index) {
size = index;
matrix = new int[index][index];
int[] v0 = { 0, 10, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] v1 = { 10, 0, 18, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, MAX_WEIGHT, 12 };
int[] v2 = { MAX_WEIGHT, 18, 0, 22, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 8 };
int[] v3 = { MAX_WEIGHT, MAX_WEIGHT, 22, 0, 20, MAX_WEIGHT, MAX_WEIGHT, 16, 21 };
int[] v4 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 20, 0, 26, MAX_WEIGHT, 7, MAX_WEIGHT };
int[] v5 = { 11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 26, 0, 17, MAX_WEIGHT, MAX_WEIGHT };
int[] v6 = { MAX_WEIGHT, 16, MAX_WEIGHT, 24, MAX_WEIGHT, 17, 0, 19, MAX_WEIGHT };
int[] v7 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, 7, MAX_WEIGHT, 19, 0, MAX_WEIGHT };
int[] v8 = { MAX_WEIGHT, 12, 8, 21, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 0 };
matrix[0] = v0;
matrix[1] = v1;
matrix[2] = v2;
matrix[3] = v3;
matrix[4] = v4;
matrix[5] = v5;
matrix[6] = v6;
matrix[7] = v7;
matrix[8] = v8;
}
public static void main(String[] args) {
MinSpanTree graph = new MinSpanTree();
graph.createGraph(9);
graph.prim();
}
} 判断是否为回路的机制没有理解
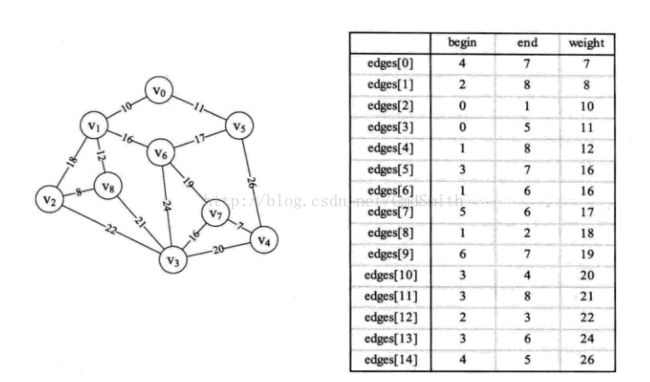
代码所示图和边集数组
代码:
public class MiniSpanTreeKruskal {
/** 邻接矩阵 */
private int[][] matrix;
/** 表示正无穷 */
private int MAX_WEIGHT = Integer.MAX_VALUE;
/**边集数组*/
private List edgeList = new ArrayList();
/**
* 创建图
*/
private void createGraph(int index) {
matrix = new int[index][index];
int[] v0 = { 0, 10, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] v1 = { 10, 0, 18, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, MAX_WEIGHT, 12 };
int[] v2 = { MAX_WEIGHT, 18, 0, 22, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 8 };
int[] v3 = { MAX_WEIGHT, MAX_WEIGHT, 22, 0, 20, MAX_WEIGHT, MAX_WEIGHT, 16, 21 };
int[] v4 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 20, 0, 26, MAX_WEIGHT, 7, MAX_WEIGHT };
int[] v5 = { 11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 26, 0, 17, MAX_WEIGHT, MAX_WEIGHT };
int[] v6 = { MAX_WEIGHT, 16, MAX_WEIGHT, 24, MAX_WEIGHT, 17, 0, 19, MAX_WEIGHT };
int[] v7 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, 7, MAX_WEIGHT, 19, 0, MAX_WEIGHT };
int[] v8 = { MAX_WEIGHT, 12, 8, 21, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 0 };
matrix[0] = v0;
matrix[1] = v1;
matrix[2] = v2;
matrix[3] = v3;
matrix[4] = v4;
matrix[5] = v5;
matrix[6] = v6;
matrix[7] = v7;
matrix[8] = v8;
}
/**
* 创建边集数组,并且对他们按权值从小到大排序(顺序存储结构也可以认为是数组吧)
*/
public void createEdages() {
Edge v0 = new Edge(4, 7, 7);
Edge v1 = new Edge(2, 8, 8);
Edge v2 = new Edge(0, 1, 10);
Edge v3 = new Edge(0, 5, 11);
Edge v4 = new Edge(1, 8, 12);
Edge v5 = new Edge(3, 7, 16);
Edge v6 = new Edge(1, 6, 16);
Edge v7 = new Edge(5, 6, 17);
Edge v8 = new Edge(1, 2, 18);
Edge v9 = new Edge(6, 7, 19);
Edge v10 = new Edge(3, 4, 20);
Edge v11 = new Edge(3, 8, 21);
Edge v12 = new Edge(2, 3, 22);
Edge v13 = new Edge(3, 6, 24);
Edge v14 = new Edge(4, 5, 26);
edgeList.add(v0);
edgeList.add(v1);
edgeList.add(v2);
edgeList.add(v3);
edgeList.add(v4);
edgeList.add(v5);
edgeList.add(v6);
edgeList.add(v7);
edgeList.add(v8);
edgeList.add(v9);
edgeList.add(v10);
edgeList.add(v11);
edgeList.add(v12);
edgeList.add(v13);
edgeList.add(v14);
}
// 克鲁斯卡尔算法
public void kruskal() {
//创建图和边集数组
createGraph(9);
//可以由图转出边集数组并按权从小到大排序,这里为了方便观察直接写出来了
createEdages();
//定义一个数组用来判断边与边是否形成环路
int[] parent = new int[9];
/**权值总和*/
int sum = 0;
int n, m;
//遍历边
for (int i = 0; i < edgeList.size(); i++) {
Edge edge= edgeList.get(i);
n = find(parent, edge.getBegin());
m = find(parent, edge.getEnd());
//说明形成了环路或者两个结点都在一棵树上
//注:书上没有讲解为什么这种机制可以保证形成环路,思考了半天,百度了也没有什么好的答案,研究的时间不多,就暂时就放一放吧
if (n != m) {
parent[n] = m;
System.out.println("(" + edge.getBegin() + "," + edge.getEnd() + ")" +edge.getWeight());
sum += edge.getWeight();
}
}
System.out.println("权值总和为:" + sum);
}
public int find(int[] parent, int index) {
while (parent[index] > 0) {
index = parent[index];
}
return index;
}
public static void main(String[] args) {
MiniSpanTreeKruskal graph = new MiniSpanTreeKruskal();
graph.kruskal();
}
}
class Edge {
private int begin;
private int end;
private int weight;
public Edge(int begin, int end, int weight) {
super();
this.begin = begin;
this.end = end;
this.weight = weight;
}
public int getBegin() {
return begin;
}
public void setBegin(int begin) {
this.begin = begin;
}
public int getEnd() {
return end;
}
public void setEnd(int end) {
this.end = end;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
@Override
public String toString() {
return "Edge [begin=" + begin + ", end=" + end + ", weight=" + weight + "]";
}
} 结果:
六、迪杰斯特拉(Dijkstra)算法
基本思想
通过Dijkstra计算图G中的最短路径时,需要指定起点vs(即从顶点vs开始计算)。
此外,引进两个集合S和U。S的作用是记录已求出最短路径的顶点,而U则是记录还未求出最短路径的顶点(以及该顶点到起点vs的距离)。
初始时,S中只有起点vs;U中是除vs之外的顶点,并且U中顶点的路径是"起点vs到该顶点的路径"。然后,从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。 然后,再从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。 ... 重复该操作,直到遍历完所有顶点。
操作步骤
(1) 初始时,S只包含起点vs;U包含除vs外的其他顶点,且U中顶点的距离为"起点vs到该顶点的距离"[例如,U中顶点v的距离为(vs,v)的长度,然后vs和v不相邻,则v的距离为∞]。
(2) 从U中选出"距离最短的顶点k",并将顶点k加入到S中;同时,从U中移除顶点k。
(3) 更新U中各个顶点到起点vs的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(vs,v)的距离可能大于(vs,k)+(k,v)的距离。
(4) 重复步骤(2)和(3),直到遍历完所有顶点。
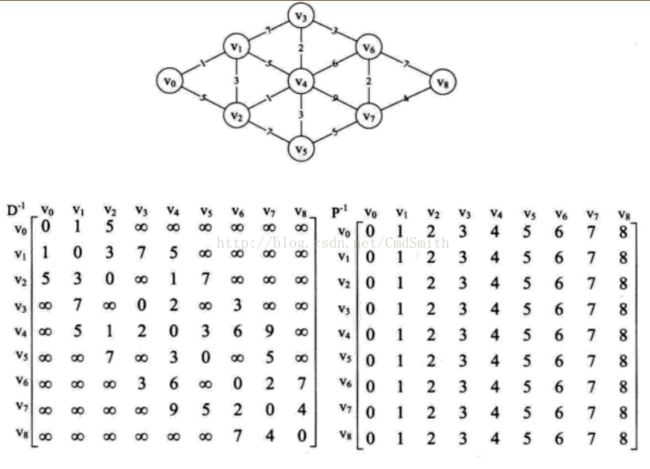
代码示例图:
图一:
图二:
代码:
public class ShortestPathDijkstra {
/** 邻接矩阵 */
private int[][] matrix;
/** 表示正无穷 */
private int MAX_WEIGHT = Integer.MAX_VALUE;
/** 顶点集合 */
private String[] vertexes;
/**
* 创建图2
*/
private void createGraph2(int index) {
matrix = new int[index][index];
vertexes = new String[index];
int[] v0 = { 0, 1, 5, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] v1 = { 1, 0, 3, 7, 5, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] v2 = { 5, 3, 0, MAX_WEIGHT, 1, 7, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] v3 = { MAX_WEIGHT, 7, MAX_WEIGHT, 0, 2, MAX_WEIGHT, 3, MAX_WEIGHT, MAX_WEIGHT };
int[] v4 = { MAX_WEIGHT, 5, 1, 2, 0, 3, 6, 9, MAX_WEIGHT };
int[] v5 = { MAX_WEIGHT, MAX_WEIGHT, 7, MAX_WEIGHT, 3, 0, MAX_WEIGHT, 5, MAX_WEIGHT };
int[] v6 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 3, 6, MAX_WEIGHT, 0, 2, 7 };
int[] v7 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 9, 5, 2, 0, 4 };
int[] v8 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 7, 4, 0 };
matrix[0] = v0;
matrix[1] = v1;
matrix[2] = v2;
matrix[3] = v3;
matrix[4] = v4;
matrix[5] = v5;
matrix[6] = v6;
matrix[7] = v7;
matrix[8] = v8;
vertexes[0] = "v0";
vertexes[1] = "v1";
vertexes[2] = "v2";
vertexes[3] = "v3";
vertexes[4] = "v4";
vertexes[5] = "v5";
vertexes[6] = "v6";
vertexes[7] = "v7";
vertexes[8] = "v8";
}
/**
* 创建图1
*/
private void createGraph1(int index) {
matrix = new int[index][index];
vertexes = new String[index];
int[] v0 = { 0, 1, MAX_WEIGHT, MAX_WEIGHT, 2, MAX_WEIGHT };
int[] v1 = { 1, 0, 1, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] v2 = { MAX_WEIGHT, 1, 0, 1, MAX_WEIGHT, MAX_WEIGHT };
int[] v3 = { MAX_WEIGHT, MAX_WEIGHT, 1, 0, 1, MAX_WEIGHT };
int[] v4 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 1, 0, 1 };
int[] v5 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 1, 1, 0 };
matrix[0] = v0;
matrix[1] = v1;
matrix[2] = v2;
matrix[3] = v3;
matrix[4] = v4;
matrix[5] = v5;
vertexes[0] = "A";
vertexes[1] = "B";
vertexes[2] = "C";
vertexes[3] = "D";
vertexes[4] = "E";
vertexes[5] = "F";
}
/**
* Dijkstra最短路径。
*
* vs -- 起始顶点(start vertex) 即,统计图中"顶点vs"到其它各个顶点的最短路径。
*/
public void dijkstra(int vs) {
// flag[i]=true表示"顶点vs"到"顶点i"的最短路径已成功获取
boolean[] flag = new boolean[vertexes.length];
// U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离),与 flag配合使用,flag[i] == true 表示U中i顶点已被移除
int[] U = new int[vertexes.length];
// 前驱顶点数组,即,prev[i]的值是"顶点vs"到"顶点i"的最短路径所经历的全部顶点中,位于"顶点i"之前的那个顶点。
int[] prev = new int[vertexes.length];
// S的作用是记录已求出最短路径的顶点
String[] S = new String[vertexes.length];
// 步骤一:初始时,S中只有起点vs;U中是除vs之外的顶点,并且U中顶点的路径是"起点vs到该顶点的路径"。
for (int i = 0; i < vertexes.length; i++) {
flag[i] = false; // 顶点i的最短路径还没获取到。
U[i] = matrix[vs][i]; // 顶点i与顶点vs的初始距离为"顶点vs"到"顶点i"的权。也就是邻接矩阵vs行的数据。
prev[i] = 0; //顶点i的前驱顶点为0
}
// 将vs从U中“移除”(U与flag配合使用)
flag[vs] = true;
U[vs] = 0;
// 将vs顶点加入S
S[0] = vertexes[vs];
// 步骤一结束
//步骤四:重复步骤二三,直到遍历完所有顶点。
// 遍历vertexes.length-1次;每次找出一个顶点的最短路径。
int k = 0;
for (int i = 1; i < vertexes.length; i++) {
// 步骤二:从U中找出路径最短的顶点,并将其加入到S中(如果vs顶点到x顶点还有更短的路径的话,那么
// 必然会有一个y顶点到vs顶点的路径比前者更短且没有加入S中
// 所以,U中路径最短顶点的路径就是该顶点的最短路径)
// 即,在未获取最短路径的顶点中,找到离vs最近的顶点(k)。
int min = MAX_WEIGHT;
for (int j = 0; j < vertexes.length; j++) {
if (flag[j] == false && U[j] < min) {
min = U[j];
k = j;
}
}
//将k放入S中
S[i] = vertexes[k];
//步骤二结束
//步骤三:更新U中的顶点和顶点对应的路径
//标记"顶点k"为已经获取到最短路径(更新U中的顶点,即将k顶点对应的flag标记为true)
flag[k] = true;
//修正当前最短路径和前驱顶点(更新U中剩余顶点对应的路径)
//即,当已经"顶点k的最短路径"之后,更新"未获取最短路径的顶点的最短路径和前驱顶点"。
for (int j = 0; j < vertexes.length; j++) {
//以k顶点所在位置连线其他顶点,判断其他顶点经过最短路径顶点k到达vs顶点是否小于目前的最短路径,是,更新入U,不是,不做处理
int tmp = (matrix[k][j] == MAX_WEIGHT ? MAX_WEIGHT : (min + matrix[k][j]));
if (flag[j] == false && (tmp < U[j])) {
U[j] = tmp;
//更新 j顶点的最短路径前驱顶点为k
prev[j] = k;
}
}
//步骤三结束
}
//步骤四结束
// 打印dijkstra最短路径的结果
System.out.println("起始顶点:" + vertexes[vs]);
for (int i = 0; i < vertexes.length; i++) {
System.out.print("最短路径(" + vertexes[vs] + "," + vertexes[i] + "):" + U[i] + " ");
List path = new ArrayList<>();
int j = i;
while (true) {
path.add(vertexes[j]);
if (j == 0)
break;
j = prev[j];
}
for (int x = path.size()-1; x >= 0; x--) {
if (x == 0) {
System.out.println(path.get(x));
} else {
System.out.print(path.get(x) + "->");
}
}
}
System.out.println("顶点放入S中的顺序:");
for (int i = 0; i< vertexes.length; i++) {
System.out.print(S[i]);
if (i != vertexes.length-1)
System.out.print("-->");
}
}
public static void main(String[] args) {
ShortestPathDijkstra dij = new ShortestPathDijkstra();
dij.createGraph1(6);
// dij.createGraph2(9);
dij.dijkstra(0);
}
} 运行结果:
图一
图二
七、弗洛伊德(Floyd)算法
代码所示图:
图1:
图2:
代码:
public class ShortestPathFloyd {
/** 邻接矩阵 */
private int[][] matrix;
/** 表示正无穷 */
private int MAX_WEIGHT = Integer.MAX_VALUE;
/**路径矩阵*/
private int[][] pathMatirx;
/**前驱表*/
private int[][] preTable;
/**
* 创建图2
*/
private void createGraph2(int index) {
matrix = new int[index][index];
int[] v0 = { 0, 1, 5, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] v1 = { 1, 0, 3, 7, 5, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] v2 = { 5, 3, 0, MAX_WEIGHT, 1, 7, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] v3 = { MAX_WEIGHT, 7, MAX_WEIGHT, 0, 2, MAX_WEIGHT, 3, MAX_WEIGHT, MAX_WEIGHT };
int[] v4 = { MAX_WEIGHT, 5, 1, 2, 0, 3, 6, 9, MAX_WEIGHT };
int[] v5 = { MAX_WEIGHT, MAX_WEIGHT, 7, MAX_WEIGHT, 3, 0, MAX_WEIGHT, 5, MAX_WEIGHT };
int[] v6 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 3, 6, MAX_WEIGHT, 0, 2, 7 };
int[] v7 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 9, 5, 2, 0, 4 };
int[] v8 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 7, 4, 0 };
matrix[0] = v0;
matrix[1] = v1;
matrix[2] = v2;
matrix[3] = v3;
matrix[4] = v4;
matrix[5] = v5;
matrix[6] = v6;
matrix[7] = v7;
matrix[8] = v8;
}
/**
* 创建图1
*/
private void createGraph1(int index) {
matrix = new int[index][index];
int[] v0 = { 0, 1, MAX_WEIGHT, MAX_WEIGHT, 2, MAX_WEIGHT };
int[] v1 = { 1, 0, 1, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] v2 = { MAX_WEIGHT, 1, 0, 1, MAX_WEIGHT, MAX_WEIGHT };
int[] v3 = { MAX_WEIGHT, MAX_WEIGHT, 1, 0, 1, MAX_WEIGHT };
int[] v4 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 1, 0, 1 };
int[] v5 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 1, 1, 0 };
matrix[0] = v0;
matrix[1] = v1;
matrix[2] = v2;
matrix[3] = v3;
matrix[4] = v4;
matrix[5] = v5;
}
public void floyd(){
//路径矩阵(D),表示顶点到顶点的最短路径权值之和的矩阵,初始时,就是图的邻接矩阵。
pathMatirx = new int[matrix.length][matrix.length];
//前驱表(P),P[m][n] 的值为 m到n的最短路径的前驱顶点,如果是直连,值为n。也就是初始值
preTable = new int[matrix.length][matrix.length];
//初始化D,P
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix.length; j++) {
pathMatirx[i][j] = matrix[i][j];
preTable[i][j] = j;
}
}
//循环 中间经过顶点
for (int k = 0; k < matrix.length; k++) {
//循环所有路径
for (int m = 0; m < matrix.length; m++) {
for (int n = 0; n < matrix.length; n++) {
int mn = pathMatirx[m][n];
int mk = pathMatirx[m][k];
int kn = pathMatirx[k][n];
int addedPath = (mk == MAX_WEIGHT || kn == MAX_WEIGHT)? MAX_WEIGHT : mk + kn;
if (mn > addedPath) {
//如果经过k顶点路径比原两点路径更短,将两点间权值设为更小的一个
pathMatirx[m][n] = addedPath;
//前驱设置为经过下标为k的顶点
preTable[m][n] = preTable[m][k];
}
}
}
}
}
/**
* 打印 所有最短路径
*/
public void print() {
for (int m = 0; m < matrix.length; m++) {
for (int n = m + 1; n < matrix.length; n++) {
int k = preTable[m][n];
System.out.print("(" + m + "," + n + ")" + pathMatirx[m][n] + ": ");
System.out.print(m);
while (k != n) {
System.out.print("->" + k);
k = preTable[k][n];
}
System.out.println("->" + n);
}
System.out.println();
}
}
public static void main(String[] args) {
ShortestPathFloyd floyd = new ShortestPathFloyd();
floyd.createGraph2(9);
// floyd.createGraph1(6);
floyd.floyd();
floyd.print();
} 结果:
图1:
图2:
(0,1)1: 0->1
(0,2)4: 0->1->2
(0,3)7: 0->1->2->4->3
(0,4)5: 0->1->2->4
(0,5)8: 0->1->2->4->5
(0,6)10: 0->1->2->4->3->6
(0,7)12: 0->1->2->4->3->6->7
(0,8)16: 0->1->2->4->3->6->7->8
(1,2)3: 1->2
(1,3)6: 1->2->4->3
(1,4)4: 1->2->4
(1,5)7: 1->2->4->5
(1,6)9: 1->2->4->3->6
(1,7)11: 1->2->4->3->6->7
(1,8)15: 1->2->4->3->6->7->8
(2,3)3: 2->4->3
(2,4)1: 2->4
(2,5)4: 2->4->5
(2,6)6: 2->4->3->6
(2,7)8: 2->4->3->6->7
(2,8)12: 2->4->3->6->7->8
(3,4)2: 3->4
(3,5)5: 3->4->5
(3,6)3: 3->6
(3,7)5: 3->6->7
(3,8)9: 3->6->7->8
(4,5)3: 4->5
(4,6)5: 4->3->6
(4,7)7: 4->3->6->7
(4,8)11: 4->3->6->7->8
(5,6)7: 5->7->6
(5,7)5: 5->7
(5,8)9: 5->7->8
(6,7)2: 6->7
(6,8)6: 6->7->8
(7,8)4: 7->8