优选队列（堆）------二叉堆

前言

譬如打印机打印作业的操作，一般是放到队列中，按照先后的顺序来，但是总有一些操作时间的短的，如果排的比较靠后，也要等好长时间，我们希望这些花费时间短的能够优先操作，这就需要队列特殊的处理，我们称为优先队列（priority quenue）。
我们将讨论：

• 优先队列ADT的有效实现
• 优先队列的使用‘
• 优先队列的高级实现

1. 二叉堆

二叉堆的使用对于优先队列的实现相当普遍，像二叉树一样，它也有两个性质，结构性质和堆序性质。

1.1 结构性质

• 一棵被完全填满的二叉树，即完全二叉树；
• 高为 h的树，有 $2^h$ 到 $2^{k+1}-1$ 个节点；
• 深度为 $O(logN)$；
• 可以用数组表示，从数组下标 1 开始，对于数组上任意 位置 $i$ ，其左儿子在位置 $2i$上，右儿子在 $2i+1$上；

上边数组 第2个元素是 21 ，它的左孩子在第4个，是 24，右孩子在 第5个，是31。

1.2 堆序性质

分为最小和最大两种类型，我们都以最小的为例

• 最小元在根上
• 任意节点小于它的所有后裔

1.3 堆序操作

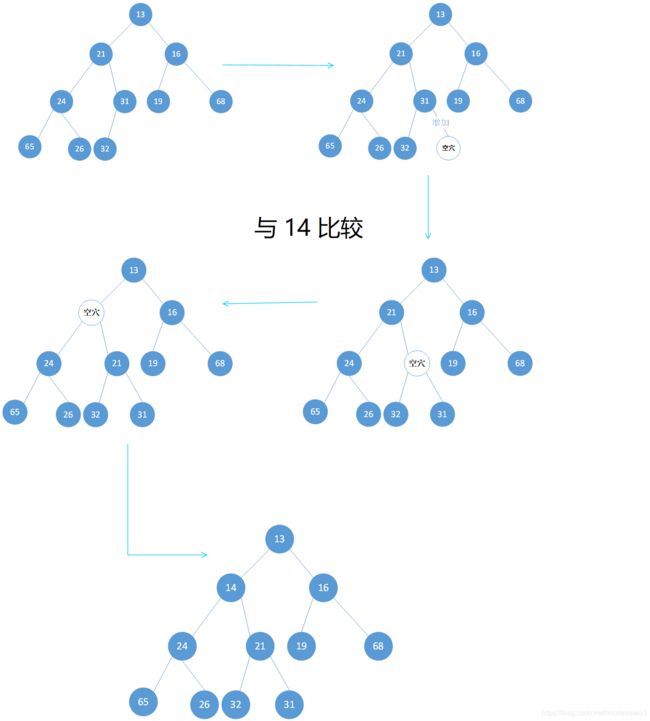
insert 插入

• 在下一个可用位置，创建一个空穴，如果插入的新元素放入不破坏堆序，就插入完成
• 否则，把空穴父节点元素移到空穴，这样空穴就上冒一步，这种策略叫上滤
• 继续该过程，直到成功

如下，插入 14

主要代码为：

public void insert(T x){
        if(currentSize==array.length-1){
            enlargeArray(2*array.length-1);
        }
        int hole=++currentSize;
        for(array[0]=x;x.compareTo(array[hole/2])<0;hole/=2){
            array[hole]=array[hole/2];
        }
        array[hole]=x;
    }

这里我们把数组下标为0的位置，放最新插入的 项
其他 insert方式：也可以直接将 14 插入到空穴，然后通过反复执行交换达到平衡，如果一个元素上滤到 d层，就需要 3d次赋值，而我们 只要d+1次。

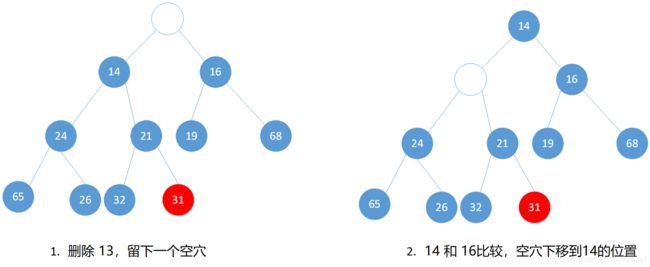
deleteMin删除最小
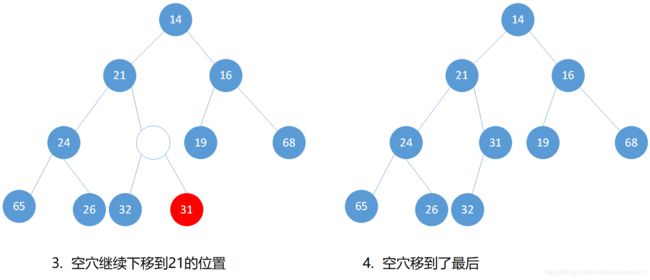
上边的最小元是根节点的 13，删除它是简单的，花费时间$O(1)$，但 复杂的是继续保持堆序性，由于少了一个节点，必须给最后一个节点 31 找一个合适的位置。
我们这样操作，删除根节点后根节点变为空穴，然后让空穴下滤，知道将空穴移到最后。

主要代码为：

public void percolateDowm(int hole){
        int child;
        T tmp = array[hole];  //暂存空洞节点的值

        for(; hole*2 <= currentSize; hole = child){ //对子树遍历进行
            child = hole*2;
            if (child != currentSize && array[child+1].compareTo(array[child])<0) //找出两个子节点中的较小者
                child++;
            if (array[child].compareTo(tmp)<0)  //子节点较小者与空洞值相比
                array[hole] = array[child];
            else
                break;
        }
        array[hole] = tmp;
    }

BuildHeap 构造堆
之前的插入都是单个元素插入的，现在给定了一个数组，我们可以把它直接放到堆里，然后从下层开始每个父节点依次调整位置，构造堆序，堆排序就是这种思路，比如给定数组元素：

• $150,80,40,30,10,70,110,100,20,90,60,50,120,140,130$
  放入堆初始状态为：

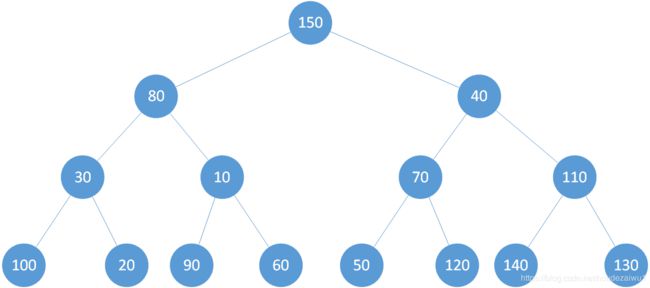
110 的节点都比两个孩子节点值小，不用调整位置；
然后是 70 的节点，调整后为

节点 10 不用调整，然后是 30 的节点

然后是 40 节点的，不用变，
80的节点 调整后

最后 是 根节点，做到这里，我们发现，父节点和子节点交换后，子节点要重新调整自己的堆序以达到平衡。

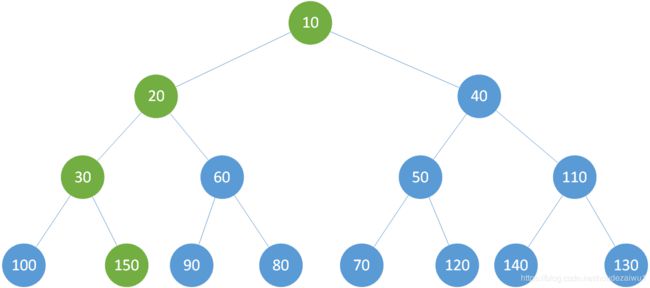
只主要代码为：

public void percolateDowm(int hole){
        int child;
        T tmp = array[hole];  //暂存空洞节点的值

        for(; hole*2 <= currentSize; hole = child){ //对子树遍历进行
            child = hole*2;
            if (child != currentSize && array[child+1].compareTo(array[child])<0) //找出两个子节点中的较小者
                child++;
            if (array[child].compareTo(tmp)<0)  //子节点较小者与空洞值相比
                array[hole] = array[child];
            else
                break;
        }
        array[hole] = tmp;
    }

1.4 完整实现代码

package 优先队列堆.二叉堆;

public class BinaryHeap > {
    private static final int Default_CAPACITY = 10;
    private int currentSize; // 当前二叉堆中的元素个数，不是数组的大小
    private T[] array; // 二叉堆所在数组
    public BinaryHeap() {
        this(Default_CAPACITY);
    }
    public BinaryHeap( int capacity) {
        makeEmpty();
        enlargeArray(capacity);
    }
    /**
     * 二叉堆的构造方法
     * @param items
     */
    public BinaryHeap(T []items) {
        currentSize = items.length;
        array = (T[]) new Comparable[(currentSize+2)*11/10];
        int i=1;
        for (T item:items)
            array[i++]=item;
        buildHeap();
    }
    private void buildHeap(){
        for (int i = currentSize/2; i >0 ; i--) {
            percolateDowm(i);
        }
    }
    private void enlargeArray(int newSize){
        T[] oldArray=array;
        if(newSize

1.5 测试类

package 优先队列堆.二叉堆;

import java.util.Arrays;

public class Test {
    public static void main(String[] args) {

        BinaryHeap binaryHeap = new BinaryHeap<>();
        binaryHeap.insert(13);
        binaryHeap.insert(21);
        binaryHeap.insert(16);
        binaryHeap.insert(24);
        binaryHeap.insert(31);
        binaryHeap.insert(19);
        binaryHeap.insert(68);
        binaryHeap.insert(65);
        binaryHeap.insert(26);
        binaryHeap.insert(32);
        Comparable[] array =  binaryHeap.getArray();
        System.out.println("单个插入的："+Arrays.deepToString(array));
        binaryHeap.deleteMin();
        System.out.println("删除最小后："+Arrays.deepToString(array));
        Integer[] items = {150,80,40,30,10,70,110,100,20,90,60,50,120,140,130};
        BinaryHeap binaryHeap2 = new BinaryHeap<>(items);
        Comparable[] array2 = binaryHeap2.getArray();
        System.out.println("用数组构造的："+Arrays.deepToString(array2));


    }
}

结果

单个插入的数组第一个放的是最新插入的，请忽略，从第二个开始读

单个插入的：[32, 13, 21, 16, 24, 31, 19, 68, 65, 26, 32, null, null, null, null, null, null, null, null]
删除最小后：[32, 16, 21, 19, 24, 31, 32, 68, 65, 26, 32, null, null, null, null, null, null, null, null]
用数组构造的：[null, 10, 20, 40, 30, 60, 50, 110, 100, 150, 90, 80, 70, 120, 140, 130, null, null]