Matlab求解微分方程数值解

有三种方法求解微分方程数值解：

• 欧拉法
• 改进欧拉法
• 龙格库塔法

接下来用一个练习来对比这三种求解方法。

问题描述：用改进的Euler方法、MATLAB的ode45命令分别求下列初值问题的数值解，并画图与精确解对比，其中步长=0.1。而方程的精确解为 y=1(1−34e−2x)−−−−−−−√
通过精确解和使用上面三种方法求解的结果进行比对，来判断哪种方法求解的结果更加精确。

欧拉法：

函数代码如下：

% f为句柄，y0为f(0)，[x0,xn]为x范围，hh为步长
function [yy] = euler(f,y0, x0, xn, hh)

% 求出离散点个数
len = (xn - x0)/hh;

% 初始化
x(1) = x0;
y(1) = y0;
for i=2:len+1
    x(i) = x(i-1) + hh;
    h(i) = x(i) - x(i-1);
end

% 计算y
for i=2:len+1
    y(i) = y(i-1)+h(i)*f(x(i-1), y(i-1));
end

% 赋给函数返回值
yy = y;

测试代码如下：

% 函数句柄
f = @(x,y) y*(1-y^2);

% 调用欧拉函数
yy = euler(f, 2, 0, 10, 0.1);
x = 0:0.1:10;

% 画出欧拉法计算出来的离散点的图
plot(x,yy,'r')
hold on

% 画出精确解的离散图
X = 0:0.1:10;
Y = sqrt(1./(1-(3./4).*exp(-2.*X)));
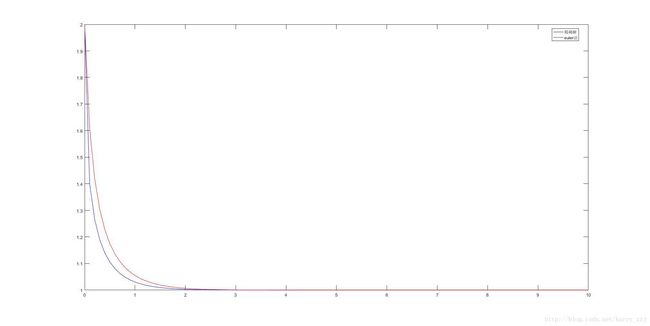
plot(X,Y, 'b')

对比图如下：

可以从图上看出误差较大

改进欧拉法：

函数代码如下：

% f为句柄，y0为f(0)，[x0,xn]为x范围，hh为步长
function[yy] = euler_correct(f, y0, x0, xn, hh)

% 计算离散点个数
len = (xn - x0)/hh;

%初始化
x_ave(1) = x0;
for i=2:len+1
    x_ave(i) = x_ave(i-1) + hh;
    h(i) = x_ave(i) - x_ave(i-1);
end

y_ave(1) = y0;
for i=2:len+1
    y_ave(i) = y_ave(i-1)+h(i)*f(x_ave(i-1), y_ave(i-1));
end

% 求出改进欧拉法的y
y(1) = y0;
for i=2:len+1
   y(i) = y(i-1)+h(i)*(f(x_ave(i-1), y(i-1)) + f(x_ave(i), y_ave(i)))/2;
end

yy = y;

测试代码：

clc, clear
f = @(x,y) y*(1-y^2);
% 调用函数
yy = euler_correct(f, 2, 0, 10, 0.1);
x = 0:0.1:10;
% 画出改进欧拉离散图
plot(x,yy,'r')
hold on

% 画出精确解的图
X = 0:0.1:10;
Y = sqrt(1./(1-(3./4).*exp(-2.*X)));
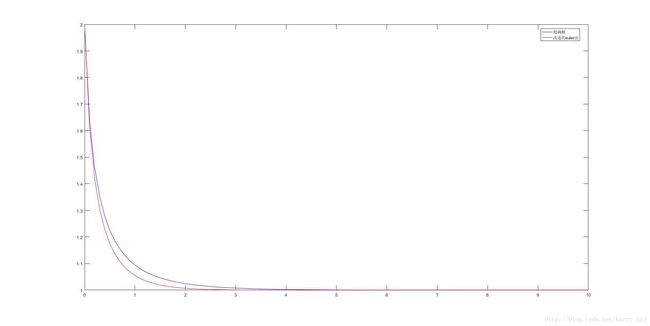
plot(X,Y, 'b')

对比图如下：

龙格库塔算法

代码如下：

% 精确解
X = 0:0.1:10;
Y = sqrt(1./(1-(3./4).*exp(-2.*X)));
plot(X,Y, 'b')

hold on

% 龙格库塔算法
doty = @(x,y) y*(1-y^2);
[x,y] = ode45(doty,[0:0.1:10],2)
plot(x,y,'r')

对比图如下：