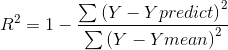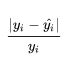机器学习模型，评估指标之回归模型---公式+优缺点+代码

机器学习模型评价指标大概有

1、回归的：RMSE(平方根误差)、MAE（平均绝对误差）、MSE(平均平方误差)、Coefficient of determination (决定系数R2)、 MAPE（平均绝对百分误差）、MSLE（均方根对数误差）等。

2、分类的：混淆矩阵、精确率、召回率、准确率、F1值、ROC-AUC 、PRC、G-MEAN等。

3、聚类的：兰德指数、互信息、轮廓系数等。

本篇主要记录回归模型的评估指标，为什么先写回归？因为上个项目使用了回归模型，就近。在学习python，算法等技能的过程中，站在前辈们的肩膀上明白了很多知识的应用。待时间如丝线缓缓，攒起幸福的模样，学习是个积累的过程，接下来我会慢慢的整理出笔记本里的要点及部分项目 (习惯本地保存文件)。若有不正之处，尽请指教。

目录

1评估指标

绝对误差与相对误差

Mean absolute error  MAE（平均绝对误差）

Mean squared error  MSE（均方误差）

Root Mean squared error  RMSE（均方根误差）

Mean squared logarithmic error  MSLE（均方根对数误差）

Mean Absolute Percentage Error   MAPE（平均绝对百分误差）

R-square(决定系数) Coefficient of determination                                                                               

Adjusted R-Square (校正决定系数）

Median absolute error（中位数绝对误差）

explained_variance_score(解释方差分)

2 解决评估指标鲁棒性问题

3 参考文档

变量解释：Y 真实值，Ypredict  预测值，Ymean  目标数据均值,  n 样本数  ，p 特征数

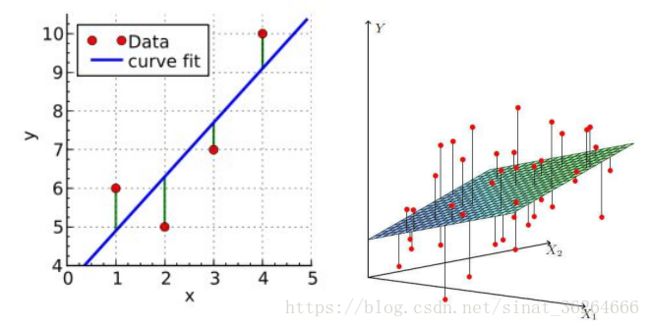
以下为一元变量和二元变量的线性回归示意图：

 

首先了解下回归分析3种误差

SSR(回归平方和)  The sum of squares for regression   ，是估计值与平均值的误差

                                                                       SSR=

SSE(误差平方和)    The sum of squares for  error ，估计值与真实值的误差，随着样本增加，SSE必然增加，也就是说，不同的数据集的情况下，SSE比较没有意义,所以需要有前提条件。同样的数据集的情况下，SSE越小，误差越小，模型效果越好。

                                                                       SSE=

SST(总离差平方和)  The sum of squares for total ，平均值与真实值的误差，它反映了与数学期望的偏离程度，样本分散程度

                                                                       SSR=

回归问题衡量的是预测出Y对于真实Y的差距。通过差距辅助判断预测结果的准确性。预测值和真实值2组数据，利用均值之差进行统计推断，背后的原理 ，是方差分析的思想。绝对误差指标衡量了一组数据 与 另外一组数据的均值  差的绝对值 之和，我们南方妹子平均身高165cm(可能还稍低一些，捂脸)，另外一组175cm 左右样本，差值之和，不用算，根据之前的经验，结果显而易见，她们就是一组小仙女和一组高仙女，不一样不一样。

1评估指标

• 绝对误差与相对误差

                                                                      绝对误差= Y - Ypredict 

                                                                      相对误差 

 绝对误差是从极差发展而来的。极差是最大值－最小值，最初用极差来评价一组数据的离散度。因为由两个数据来评判一组数据是不科学的，所以从极差进行改进，改用绝对误差之和。

（1）为避免出现绝对误差总和为零，所以对绝对误差 求绝对值，求平方。
（2）而为避免指标受样本含量的影响，所以除以样本数，求平均值。

• Mean absolute error  MAE（平均绝对误差）

平均绝对误差（Mean Absolute Error,MAE),又称为L1范数损失。用于评估预测结果和真实数据集的接近程度，其值越小说明拟合效果越好。可以更好地反映预测值误差的实际情况。

                                                                     MAE=    ∑ |Y - Ypredict|

优点：可以把绝对误差和相对误差里面正负相互抵消的问题去掉。

缺点：绝对值的存在导致函数不光滑，在某些点上不能求导

#mean_absolute_error
from sklearn.metrics import mean_absolute_error
y_true=[3,0.5,2,7]
y_pred=[2.5,0.0,2,8]
print(mean_absolute_error(y_true,y_pred))

y_true=[[0.5,1],[-1,1],[7,-6]]
y_pred=[[0,2],[-1,2],[8,-5]]
print(mean_absolute_error(y_true,y_pred))
print(mean_absolute_error(y_true,y_pred,multioutput="raw_values"))
print(mean_absolute_error(y_true,y_pred,multioutput=[0.3,0.7]))

#结果
#0.5
#0.75
#[ 0.5  1. ]
#0.85

• Mean squared error  MSE（均方误差）

均方差（Mean squared error，MSE）L2范数损失，该指标计算的是拟合数据和原始数据对应样本点的误差的平方和的均值，其值越小说明拟合效果越好。常被用作线性回归的损失函数。

                                                                     MSE=    

优点：解决了不光滑的问题（即不可导问题）。

缺点：MSE与我们的目标变量的量纲不一致，为了保证量纲一致性，我们需要对MSE进行开方，得到RMSE。

#mean_squared_error
from sklearn.metrics import mean_squared_error
y_true=[3,-0.5,2,7]
y_pred=[2.5,0.0,2,8]
print(mean_squared_error(y_true,y_pred))
y_true=[[0.5,1],[-1,1],[7,-6]]
y_pred=[[0,2],[-1,2],[8,-5]]
print(mean_squared_error(y_true,y_pred))

#结果
#0.375
#0.708333333333

• Root Mean squared error  RMSE（均方根误差）

常用来作为机器学习模型预测结果衡量的标准。MSE加了个根号，这样数量级上比较直观，比如RMSE=10，可以认为回归效果相比真实值平均相差10。

                                                                    RMSE=    

优点：解决了上述的缺点。

缺点：它是使用平均误差，而平均值对异常点（outliers）较敏感，如果回归器对某个点的回归值很不理想，那么它的误差则较大，从而会对RMSE的值有较大影响，即平均值是非鲁棒的。受到量纲化影响

 RMSE与MAE对比：RMSE相当于L2范数，MAE相当于L1范数。次数越高，计算结果就越与较大的值有关，而忽略较小的值，所以这就是为什么RMSE针对异常值更敏感的原因（即有一个预测值与真实值相差很大，那么RMSE就会很大）。

from sklearn.metrics import mean_squared_error
import numpy as np
 
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
MSE = mean_squared_error(y_true, y_pred)
RMSE = np.sqrt(MSE )
print(RMSE)

 

• Mean squared logarithmic error  MSLE（均方根对数误差）

当目标实现指数增长时，例如人口数量、一种商品在几年时间内的平均销量等，这个指标最适合使用。请注意，这个指标惩罚的是一个被低估的估计大于被高估的估计。

                                                                        

from sklearn.metrics import mean_squared_log_error
y_true = [3, 5, 2.5, 7]
y_pred = [2.5, 5, 4, 8]
mean_squared_log_error(y_true, y_pred)  
0.039...
y_true = [[0.5, 1], [1, 2], [7, 6]]
y_pred = [[0.5, 2], [1, 2.5], [8, 8]]
mean_squared_log_error(y_true, y_pred)  
0.044...

 

• Mean Absolute Percentage Error   MAPE（平均绝对百分误差）

                                                                        

MAPE相比于MSE和RMSE，不易受个别离群点影响，鲁棒性更强。                                                                

import numpy as np 
def mape(y_true, y_pred): """
    参数:
    y_true -- 测试集目标真实值
    y_pred -- 测试集目标预测值
    
    返回:
    mape -- MAPE 评价指标
    """ 
    n = len(y_true) 
    mape = sum(np.abs((y_true - y_pred)/y_true))/n*100 
    return mape

• R-square(决定系数) Coefficient of determination                                                                               

                                                                

                                                                             

   R方一个综合评估的指标，可以理解为因变量y中的变异性能能够被估计的多元回归方程解释的比例，它衡量各个自变量对因变量变动的解释程度，分母理解为原始数据的离散程度，分子为预测数据和原始数据的误差，二者相除可以消除原始数据离散程度的影响.其取值在0与1之间，其值越接近1，则变量的解释程度就越高，其值越接近0，其解释程度就越弱。

理论上取值范围（-∞，1], 正常取值范围为[0 1] ------实际操作中通常会选择拟合较好的曲线计算R²，因此很少出现-∞

越接近1，表明方程的变量对y的解释能力越强，这个模型对数据拟合的也较好

越接近0，表明模型拟合的越差

经验值：>0.4， 拟合效果好

优点：既考虑了预测值与真值之间的差异，也考虑了问题本身真值之间的差异，是一个归一化的度量标准。

缺点： 数据集的样本越大，R²越大，因此，不同数据集的模型结果比较会有一定的误差

#r2_score
from sklearn.metrics import r2_score
y_true=[3,-0.5,2,7]
y_pred=[2.5,0.0,2,8]
print(r2_score(y_true,y_pred))

y_true=[[0.5,1],[-1,1],[7,-6]]
y_pred=[[0,2],[-1,2],[8,-5]]
print(r2_score(y_true,y_pred,multioutput="variance_weighted"))

y_true=[[0.5,1],[-1,1],[7,-6]]
y_pred=[[0,2],[-1,2],[8,-5]]
print(r2_score(y_true,y_pred,multioutput="uniform_average"))
print(r2_score(y_true,y_pred,multioutput="raw_values"))
print(r2_score(y_true,y_pred,multioutput=[0.3,0.7]))

#结果
#0.948608137045
#0.938256658596
#0.936800526662
#[ 0.96543779  0.90816327]
#0.92534562212

• Adjusted R-Square (校正决定系数）

一般来说，增加自变量的个数，回归平方和会增加，残差平方和会减少，所以R方会增大；反之，减少自变量的个数，回归平方和减少，残差平方和增加。

为了消除自变量的数目的影响，引入了调整的R方,消除了样本数量和特征数量的影响

                                                              

import numpy as np
from sklearn.metrics import r2_score
 
y_true = [[0.5, 1], [0.1, 1], [7, 6], [7.5, 6.5]]
y_pred = [[0, 2], [0.1, 2], [8, 5], [7.2, 6.2]]
y_true_array = np.array([[0.5, 1], [0.1, 1], [7, 6], [7.5, 6.5]])
n=y_true_array.shape[0]         #样本数量
p=y_true_array.shape[1]         #特征数量
print(n,p)
r2_score01 = r2_score(y_true, y_pred, multioutput='variance_weighted')
print(r2_score01)
Adj_r2_score01 = 1-( (1-r2_score01)*(n-1) ) / (n-p-1)
print(Adj_r2_score01) 

 

• Median absolute error（中位数绝对误差）

中位数绝对误差适用于包含异常值的数据的衡量。先计算出数据与它们的中位数之间的残差（偏差），MedAE就是这些偏差的绝对值的中位数。

                                                              

绝对中位差是一种统计离差的测量。而且，是一种鲁棒统计量，比标准差更能适应数据集中的异常值。对于标准差，使用的是数据到均值的距离平方，所以大的偏差权重更大，异常值对结果也会产生重要影响。对于绝对中位差，少量的异常值不会影响最终的结果。

由于绝对中位差是一个比样本方差或者标准差更鲁棒的度量，它对于不存在均值或者方差的分布效果更好，比如柯西分布。

#median_absolute_error
from sklearn.metrics import median_absolute_error
y_true=[3,-0.5,2,7]
y_pred=[2.5,0.0,2,8]
print(median_absolute_error(y_true,y_pred))

#结果
#0.5

 

• explained_variance_score(解释方差分)

解释回归模型的方差得分，这个指标用来衡量我们模型对数据集波动的解释程度，其值取值范围是[0,1]，越接近于1说明自变量越能解释因变量的方差变化，值越小说明效果越差。

                                                                  

#explained_variance_score
from sklearn.metrics import explained_variance_score
y_true=[3,-0.5,2,7]
y_pred=[2.5,0.0,2,8]
print(explained_variance_score(y_true,y_pred))
y_true=[[0.5,1],[-1,1],[7,-6]]
y_pred=[[0,2],[-1,2],[8,-5]]
print(explained_variance_score(y_true,y_pred,multioutput="raw_values"))
print(explained_variance_score(y_true,y_pred,multioutput=[0.3,0.7]))

#结果
#0.957173447537
#[ 0.96774194  1.        ]
#0.990322580645

 

2 解决评估指标鲁棒性问题

 MAE，MSE，RMSE，决定系数等评估指标是基于误差的均值对进行评估的，均值对异常点（outliers）较敏感，如果样本中有一些异常值出现，会对以上指标的值有较大影响，即均值是非鲁棒的。

通常用一下两种方法解决评估指标的鲁棒性问题：

• 剔除异常值                设定一个相对误差 ，当该值超过一定的阈值时，则认为其是一个异常点，剔除这个异常点，将异常点剔除之后。再计算平均误差来对模型进行评价。

• 使用误差的分位数来代替                 如利用中位数来代替平均数。例如 MAPE,MAPE是一个相对误差的中位数，根据数据情况用别的分位数也行。

3 参考文档

https://blog.csdn.net/shy19890510/article/details/79375062

https://blog.csdn.net/Monk_donot_know/article/details/86614558#1__1

https://blog.csdn.net/weixin_39541558/article/details/80705006#%EF%BC%884%EF%BC%89%C2%A0Mean%20squared%20logarithmic%20error

https://www.cnblogs.com/nolonely/p/7009001.html

https://yunyaniu.blog.csdn.net/article/details/91531343

https://www.cnblogs.com/wj-1314/p/9400375.html