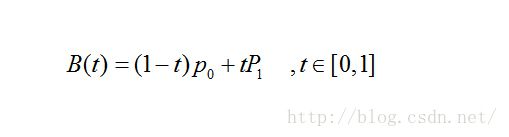Android高级绘制——绘图篇(三)路径Path绘制以及贝塞尔曲线使用技巧
开篇
废话不说了,直接开凿吧!这篇这要说一下路径(path)的绘制技巧以及 神一样的存在(贝塞尔曲线)的绘制
基本绘制
- 1、直线路径
void moveTo(float x1,float y1):直线的开始点,即将直线路径的绘制点定在(x1,y1)的位置;
void lineTo(float x2,float y2):直线的结束点,又是下一次绘制路径的开始点,lineTo() 可以一直调用
void close():如果连续画了几条直线,但没有形成闭环,调用 close() 方法会自动将路径的首尾连接起来,形成闭环。
onDraw 方法实现:
private void init() {
//初始化画笔
paint = new Paint();
paint.setTextSize(100);
paint.setColor(Color.RED);
paint.setStyle(Paint.Style.STROKE);
paint.setTextSize(100); //单位为 sp
paint.setStrokeWidth(10);
path = new Path();
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
path.moveTo(100, 200);
path.lineTo(200, 200);
path.lineTo(300, 400);
path.lineTo(0, 400);
path.close();
canvas.drawPath(path, paint);
}- 2、矩形路径
void addRect (float left, float top, float right, float bottom, Path.Direction dir)
void addRect (RectF rect, Path.Direction dir)
这里的 Path 类创建矩形路径的参数与前面 canvas 绘制矩形差不多,唯一不同的一点就是增加了 Path.Direction 参数 Path.Direction 取值: - Path.Direction.CCW:是counter-clockwise缩写,指创建逆时针方向的矩形路径 - Path.Direction.CW:是clockwise的缩写,指创建顺时针方向的矩形路径 示例代码:
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
RectF rect = new RectF(100, 200, 400, 400);
path.addRect(rect, Path.Direction.CCW);
canvas.drawPath(path, paint);
RectF rect1 = new RectF(500, 200, 800, 400);
path.addRect(rect1, Path.Direction.CW);
canvas.drawPath(path, paint);
} @Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
String text = "搞笑我们是认真的”; Path CCWPath = new Path(); RectF rect = new RectF(100, 200, 400, 400); CCWPath.addRect(rect, Path.Direction.CCW); canvas.drawPath(CCWPath, paint); canvas.drawTextOnPath(text, CCWPath, 0, 0, paint); Path CWPath = new Path(); RectF rect1 = new RectF(500, 200, 800, 400); CWPath.addRect(rect1, Path.Direction.CW); canvas.drawPath(CWPath, paint); canvas.drawTextOnPath(text, CWPath, 0, 0, paint); }- 3、圆角矩形路径
void addRoundRect (RectF rect, float[] radii, Path.Direction dir)
void addRoundRect (RectF rect, float rx, float ry, Path.Direction dir)
参数:
第一个构造函数可以定制每个角的圆角大小
- float[] radii:必须传入 8 个数值,分四组,分别对应每个角所使用的椭圆的横轴半径和纵轴半径,比如(x1,y1,x2,y2,x3,y3,x4,y4),其中,x1,y1 对应第一个角的(左上角)产生的椭圆的横轴半径和纵轴半径,其他类推
第二个构造函数:只能构建统一圆角大小
- float rx:所产生圆角的椭圆的横轴半径;
- float ry:所产生圆角的椭圆的纵轴半径;
示例代码:
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
Path CCWPath = new Path();
RectF rect = new RectF(100, 200, 400, 400);
float[] radii = {30, 30, 50, 50, 70, 70, 90, 90};
CCWPath.addRoundRect(rect, radii, Path.Direction.CCW);
canvas.drawPath(CCWPath, paint);
Path CWPath = new Path();
RectF rect1 = new RectF(500, 200, 800, 400);
CWPath.addRoundRect(rect1, 30, 30, Path.Direction.CW);
canvas.drawPath(CWPath, paint);
}
}- 4、圆形路径
void addCircle (float x, float y, float radius, Path.Direction dir)
参数:
- float x:圆心X轴坐标
- float y:圆心Y轴坐标
- float radius:圆半径
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
path.addCircle(300, 300, 200, Path.Direction.CW);
canvas.drawPath(path, paint);
}
}- 5、椭圆路径
void addOval (RectF oval, Path.Direction dir)
参数:
- RectF oval:生成椭圆所对应的矩形
- Path.Direction :生成方式,与矩形一样,分为顺时针与逆时针,意义完全相同,不再重复
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
RectF rectF = new RectF(300, 300, 700, 500);
path.addOval(rectF, Path.Direction.CW);
canvas.drawPath(path, paint);
}- 6、圆弧路径
void addArc (RectF oval, float startAngle, float sweepAngle)
参数说明:
- RectF oval:弧是椭圆的一部分,这个参数就是生成椭圆所对应的矩形;
- float startAngle:开始的角度,X轴正方向为0度
- float sweepAngel:持续的度数;
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
RectF rectF = new RectF(300, 300, 700, 500);
path.addArc(rectF, 0, 180);
canvas.drawPath(path, paint);
}Path之贝塞尔曲线以及水波纹效果
 Path 中提供了四个函数供我们实现贝塞尔曲线,我们来看一下://二阶贝赛尔
public void quadTo(float x1, float y1, float x2, float y2)
public void rQuadTo(float dx1, float dy1, float dx2, float dy2)
//三阶贝赛尔
public void cubicTo(float x1, float y1, float x2, float y2,float x3, float y3)
public void rCubicTo(float x1, float y1, float x2, float y2,float x3, float y3)1、贝塞尔曲线来源
在数学的数值分析领域中,贝赛尔曲线(Bézier曲线)是电脑图形学中相当重要的参数曲线。更高维度的广泛化贝塞尔曲线就称作贝塞尔曲面,其中贝塞尔三角是一种特殊的实例。
贝塞尔曲线于1962年,由法国工程师皮埃尔·贝塞尔(Pierre Bézier)所广泛发表,他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau算法开发,以稳定数值的方法求出贝塞尔曲线。2、贝塞尔曲线公式
一阶贝塞尔曲线
其公式可概括为:
对应的动画演示为:
P0为起点、P1为终点,t表示当前时间,B(t)表示公式的结果值。
注意,曲线的意义就是公式结果B(t)随时间的变化,其取值所形成的轨迹。在动画中,黑色点表示在当前时间t下公式B(t)的取值。而红色的那条线就不在各个时间点下不同取值的B(t)所形成的轨迹。
总而言之:对于一阶贝赛尔曲线,大家可以理解为在起始点和终点形成的这条直线上,匀速移动的点。
二阶贝塞尔曲线
公式(同样看不懂):
![]()
动画演示:
在这里P0是起始点,P2是终点,P1是控制点
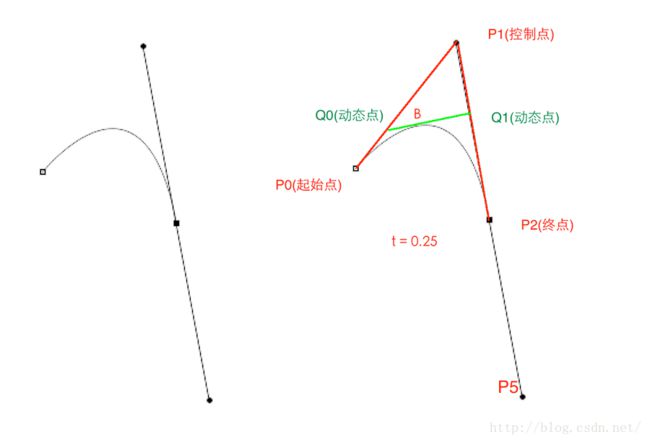
假设将时间定在t=0.25的时刻,此时的状态如下图所示:
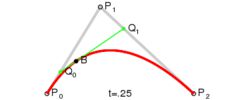
首先,P0点和P1点形成了一条贝赛尔曲线,还记得我们上面对一阶贝赛尔曲线的总结么:就是一个点在这条直线上做匀速运动;所以P0-P1这条直线上的移动的点就是Q0;
同样,P1,P2形成了一条一阶贝赛尔曲线,在这条一阶贝赛尔曲线上,它们的随时间移动的点是Q1
最后,动态点Q0和Q1又形成了一条一阶贝赛尔曲线,在它们这条一阶贝赛尔曲线动态移动的点是B
而B的移动轨迹就是这个二阶贝赛尔曲线的最终形态。从上面的讲解大家也可以知道,之所以叫它二阶贝赛尔曲线是因为,B的移动轨迹是建立在两个一阶贝赛尔曲线的中间点Q0,Q1的基础上的。
在理解了二阶贝赛尔曲线的形成原理以后,我们就不难理解三阶贝赛尔曲线了
三阶贝塞尔曲线
公式:
![]()
动画演示
同样,我们取其中一点来讲解轨迹的形成原理,当t=0.25时,此时状态如下:
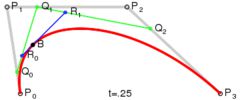
同样,P0是起始点,P3是终点;P1是第一个控制点,P2是第二个控制点;
首先,这里有三条一阶贝赛尔曲线,分别是P0-P1,P1-P2,P2-P3;
他们随时间变化的点分别为Q0,Q1,Q2
然后是由Q0,Q1,Q2这三个点,再次连接,形成了两条一阶贝赛尔曲线,分别是Q0—Q1,Q1—Q2;他们随时间变化的点为R0,R1
同样,R0和R1同样可以连接形成一条一阶贝赛尔曲线,在R0—R1这条贝赛尔曲线上随时间移动的点是B
而B的移动轨迹就是这个三阶贝赛尔曲线的最终形状。
从上面的解析大家可以看出,所谓几阶贝赛尔曲线,全部是由一条条一阶贝赛尔曲线搭起来的;
在上图中,形成一阶贝赛尔曲线的直线是灰色的,形成二阶贝赛尔曲线线是绿色的,形成三阶贝赛尔曲线的线是蓝色的。
在理解了上面的二阶和三阶贝赛尔曲线以后,我们再来看几个贝赛尔曲线的动态图
四阶贝塞尔曲线
五阶贝塞尔曲线
- 3、贝塞尔曲线与 PhotoShop 钢笔工具
如果有些同学不懂PhotoShop,这篇文章可能就会有些难度了,本篇文章主要是利用PhotoShop的钢笔工具来得出具体贝塞尔图像的
这么屌的贝赛尔曲线,在专业绘图工具PhotoShop中当然会有它的踪影,它就是钢笔工具,钢笔工具所使用的路径弯曲效果就是二阶贝赛尔曲线。
我来给大家演示一下钢笔工具的用法:
我们拿最终成形的图形来看一下为什么钢笔工具是二阶贝赛尔曲线:
右图演示的假设某一点t=0.25时,动态点B的位置图
同样,这里P0是起始点,P2是终点,P1是控制点;
P0-P1、P1-P2形成了第一层的一阶贝赛尔曲线。它们随时间的动态点分别是Q0,Q1
动态点Q0,Q1又形成了第二层的一阶贝赛尔曲线,它们的动态点是B.而B的轨迹跟钢笔工具的形状是完全一样的。所以钢笔工具的拉伸效果是使用的二阶贝赛尔曲线!
这个图与上面二阶贝赛尔曲线t=0.25时的曲线差不多,大家理解起来难度也不大。
这里需要注意的是,我们在使用钢笔工具时,拖动的是P5点。其实二阶贝赛尔曲线的控制点是其对面的P1点,钢笔工具这样设计是当然是因为操作起来比较方便。
好了,对贝赛尔曲线的知识讲了那么多,下面开始实战了,看在代码中,贝赛尔曲线是怎么来做的。
Android 中贝塞尔曲线之 quadTo
在开篇中,我们已经提到,在 Path 类中有四个方法与贝塞尔曲线相关,分别是:
//二阶贝赛尔
public void quadTo(float x1, float y1, float x2, float y2)
public void rQuadTo(float dx1, float dy1, float dx2, float dy2)
//三阶贝赛尔
public void cubicTo(float x1, float y1, float x2, float y2,float x3, float y3)
public void rCubicTo(float x1, float y1, float x2, float y2,float x3, float y3) 在这四个函数中,quadTo、rQuadTo 是二阶贝塞尔曲线,cubicTo、rCubicTo 是三阶贝塞尔曲线,我们这篇文字以二阶贝塞尔曲线的 quadTo、rQuadTo为主,三阶贝塞尔曲线 cubicTo、rCubicTo 用的使用方法与二阶贝塞尔曲线类似,用处也比较少,这篇就不在细讲了
- 1、quadTo 使用原理
这部分我们先来看看quadTo函数的用法,其定义如下:
public void quadTo(float x1, float y1, float x2, float y2)
参数中(x1,y1)是控制点坐标,(x2,y2)是终点坐标
大家可能会有一个疑问:有控制点和终点坐标,那起始点是多少呢?
整条线的起始点是通过Path.moveTo(x,y)来指定的,而如果我们连续调用quadTo(),前一个quadTo()的终点,就是下一个quadTo()函数的起点;如果初始没有调用Path.moveTo(x,y)来指定起始点,则默认以控件左上角(0,0)为起始点;大家可能还是有点迷糊,下面我们就举个例子来看看
我们利用quadTo()来画下面的这条波浪线:
最关键的是如何来确定控制点的位置!前面讲过,PhotoShop中的钢笔工具是二阶贝赛尔曲线,所以我们可以利用钢笔工具来模拟画出这条波浪线来辅助确定控制点的位置
下面我们来看看这个路径轨迹中,控制点分别在哪个位置
我们先看P0-P2这条轨迹,P0是起点,假设位置坐标是(100,300),P2是终点,假充位置坐标是(300,300);在以P0为起始点,P2为终点这条二阶贝赛尔曲线上,P1是控制点,很明显P1大概在P0,P2中间的位置,所以它的X坐标应该是200,关于Y坐标,我们无法确定,但很明显的是P1在P0,P2点的上方,也就是它的Y值比它们的小,所以根据钢笔工具上面的位置,我们让P1的比P0,P2的小100;所以P1的坐标是(200,200)
同理,不难求出在P2,P4这条二阶贝赛尔曲线上,它们的控制点P3的坐标位置应该是(400,400);P3的X坐标是400是,因为P3点是P2,P4的中间点;与P3与P1距离P0-P2-P4这条直线的距离应该是相等的。P1距离P0-P2的值为100;P3距离P2-P4的距离也应该是100,这样不难算出P3的坐标应该是(400,400);
下面开始是代码部分了。
- 2、示例代码
private void init() {
//初始化画笔
paint = new Paint();
paint.setTextSize(100);
paint.setColor(Color.RED);
paint.setStyle(Paint.Style.STROKE);
paint.setTextSize(100); //单位为 sp
paint.setStrokeWidth(5);
path = new Path();
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
path.moveTo(100, 300);
path.quadTo(200, 200, 300, 300);
path.quadTo(400, 400, 500, 300);
canvas.drawPath(path, paint);
}这里最重要的就是在onDraw(Canvas canvas)中创建Path的过程,我们在上面已经提到,第一个起始点是需要调用path.moveTo(100,300)来指定的,之后后一个path.quadTo的起始点是以前一个path.quadTo的终点为起始点的。有关控制点的位置如何查找,我们上面已经利用钢笔工具给大家讲解了,这里就不再细讲。
所以,大家在自定义控件的时候,要多跟UED沟通,看他们是如何来实现这个效果的,如果是用的钢笔工具,那我们也可以效仿使用二阶贝赛尔曲线来实现。
源码在文章底部给出
通过这个例子希望大家知道两点:
- 整条线的起始点是通过Path.moveTo(x,y)来指定的,如果初始没有调用Path.moveTo(x,y)来指定起始点,则默认以控件左上角(0,0)为起始点;
- 而如果我们连续调用quadTo(),前一个quadTo()的终点,就是下一个quadTo()函数的起点;
使用贝塞尔曲线绘制手指轨迹
要实现手指轨迹其实是非常简单的,我们只需要在自定义中拦截OnTouchEvent,然后根据手指的移动轨迹来绘制Path即可。
要实现把手指的移动轨迹连接起来,最简单的方法就是直接使用Path.lineTo()就能实现把各个点连接起来。
- 1、实现方式一:Path.lineTo(x,y)
我们先来看看效果图
(1)、自定义View——CustomView
public class CustomView extends View {
private Paint paint;
private Path path;
private Path path1;
public CustomView(Context context) {
super(context);
init();
}
public CustomView(Context context, @Nullable AttributeSet attrs) {
super(context, attrs);
init();
}
public CustomView(Context context, @Nullable AttributeSet attrs, int defStyleAttr) {
super(context, attrs, defStyleAttr);
init();
}
public CustomView(Context context, @Nullable AttributeSet attrs, int defStyleAttr, int defStyleRes) {
super(context, attrs, defStyleAttr, defStyleRes);
init();
}
private void init() {
//初始化画笔
paint = new Paint();
paint.setTextSize(100);
paint.setColor(Color.RED);
paint.setStyle(Paint.Style.STROKE);
paint.setTextSize(100); //单位为 sp
paint.setStrokeWidth(5);
path = new Path();
}
@Override
public boolean onTouchEvent(MotionEvent event) {
super.onTouchEvent(event);
switch (event.getAction()) {
case MotionEvent.ACTION_DOWN:
path.moveTo(event.getX(), event.getY());
break;
case MotionEvent.ACTION_MOVE:
path.lineTo(event.getX(), event.getY());
postInvalidate();
break;
case MotionEvent.ACTION_UP:
break;
}
return true;
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
canvas.drawPath(path, paint);
}
}当用户点击屏幕的时候,我们调用mPath.moveTo(event.getX(), event.getY());然后在用户移动手指时使用mPath.lineTo(event.getX(), event.getY());将各个点串起来。然后调用postInvalidate()重绘;
Path.moveTo()和Path.lineTo()的用法,上篇已经详细介绍过,理解起来应该没什么难度,但这里有两个地方需要注意:
- 第一:有关在case MotionEvent.ACTION_DOWN时return true的问题:return true表示当前控件已经消费了下按动作,之后的ACTION_MOVE、ACTION_UP动作也会继续传递到当前控件中;如果我们在case MotionEvent.ACTION_DOWN时return false,那么后序的ACTION_MOVE、ACTION_UP动作就不会再传到这个控件来了。有关动作拦截的知识,后续会在这个系列中单独来讲,大家先期待下吧。
第二:这里重绘控件使用的是postInvalidate();而我们以前也有用Invalidate()函数的。这两个函数的作用都是用来重绘控件的,但区别是Invalidate()一定要在UI线程执行,如果不是在UI线程就会报错。而postInvalidate()则没有那么多讲究,它可以在任何线程中执行,而不必一定要是主线程。其实在postInvalidate()就是利用handler给主线程发送刷新界面的消息来实现的,所以它是可以在任何线程中执行,而不会出错。而正是因为它是通过发消息来实现的,所以它的界面刷新可能没有直接调Invalidate()刷的那么快。
所以在我们确定当前线程是主线程的情况下,还是以invalide()函数为主。当我们不确定当前要刷新页面的位置所处的线程是不是主线程的时候,还是用postInvalidate为好;(2)、使用Path.lineTo()所存在问题
上面我们虽然实现了,画出手指的移动轨迹,但我们仔细来看看画出来的图:
我们把S放大,明显看出,在两个点连接处有明显的转折,而且在S顶部位置横纵坐标变化比较快的位置,看起来跟图片这大后的马赛克一样;利用Path绘图,是不可能出现马赛克的,因为除了Bitmap以外的任何canvas绘图全部都是矢量图,也就是利用数学公式来作出来的图,无论放在多大屏幕上,都不可能会出现马赛克!这里利用Path绘图,在S顶部之所以看起来像是马赛克是因为这个S是由各个不同点之间连线写出来的,而之间并没有平滑过渡,所以当坐标变化比较剧烈时,线与线之间的转折就显得特别明显了。
所以要想优化这种效果,就得实现线与线之间的平滑过渡,很显然,二阶贝赛尔曲线就是干这个事的。下面我们就利用我们新学的Path.quadTo函数来重新实现下移动轨迹效果。
- 2、实现方式二(优化):使用Path.quadTo()函数实现过渡
我们上面讲了,使用Path.lineTo()的最大问题就是线段转折处不够平滑。Path.quadTo()可以实现平滑过渡,但使用Path.quadTo()的最大问题是,如何找到起始点和结束点。
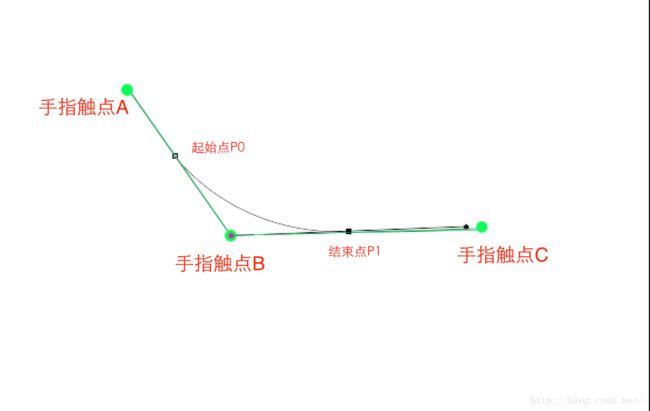
下图中,有用绿点表示的三个点,连成的两条直线,很明显他们转折处是有明显折痕的
下面我们在PhotoShop中利用钢笔工具,看如何才能实现这两条线之间的转折
从这两个线段中可以看出,我们使用Path.lineTo()的时候,是直接把手指触点A,B,C给连起来。
而钢笔工具要实现这三个点间的流畅过渡,就只能将这两个线段的中间点做为起始点和结束点,而将手指的倒数第二个触点B做为控制点。
大家可能会觉得,那这样,在结束的时候,A到P0和P1到C1的这段距离岂不是没画进去?是的,如果Path最终没有close的话,这两段距离是被抛弃掉的。因为手指间滑动时,每两个点间的距离很小,所以P1到C之间的距离可以忽略不计。
下面我们就利用这种方法在photoshop中求证,在连接多个线段时,是否能行?
在这个图形中,有很多点连成了弯弯曲曲的线段,我们利用上面我们讲的,将两个线段的中间做为二阶贝尔赛曲线的起始点和终点,把上一个手指的位置做为控制点,来看看是否真的能组成平滑的连线
整个连接过程如动画所示:
在最终的路径中看来,各个点间的连线是非常平滑的。从这里也可以看出,在为了实现平滑效果,我们只能把开头的线段一半和结束的线段的一半抛弃掉。
在讲了原理之后,下面就来看看在代码中如何来实现吧。
private void init() {
//初始化画笔
paint = new Paint();
paint.setTextSize(100);
paint.setColor(Color.RED);
paint.setStyle(Paint.Style.STROKE);
paint.setTextSize(100); //单位为 sp
paint.setStrokeWidth(5);
path = new Path();
}
@Override
public boolean onTouchEvent(MotionEvent event) {
super.onTouchEvent(event);
switch (event.getAction()) {
case MotionEvent.ACTION_DOWN:
eventX = event.getX();
eventY = event.getY();
path.moveTo(eventX, eventY);
break;
case MotionEvent.ACTION_MOVE:
float endX = event.getX();
float endY = event.getY();
path.quadTo((endX - eventX) / 2 + eventX, (endY - eventY) / 2 + eventY, endX, endY);
eventX = event.getX();
eventY = event.getY();
invalidate();
break;
case MotionEvent.ACTION_UP:
break;
}
return true;
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
canvas.drawPath(path, paint);
}最难的部分依然是onTouchEvent函数这里
public boolean onTouchEvent(MotionEvent event) {
super.onTouchEvent(event);
switch (event.getAction()) {
case MotionEvent.ACTION_DOWN:
eventX = event.getX();
eventY = event.getY();
path.moveTo(eventX, eventY);
break;
return true;在ACTION_DOWN的时候,利用 mPath.moveTo(event.getX(),event.getY())将Path的初始位置设置到手指的触点处,如果不调用mPath.moveTo的话,会默认是从(0,0)开始的。然后我们定义两个变量eventX,eventY来表示手指的前一个点。我们通过上面的分析知道,这个点是用来做控制点的。最后return true让ACTION_MOVE,ACTION_UP事件继续向这个控件传递。
在ACTION_MOVE时:
case MotionEvent.ACTION_MOVE:
float endX = event.getX();
float endY = event.getY();
path.quadTo((endX - eventX) / 2 + eventX, (endY - eventY) / 2 + eventY, endX, endY);
eventX = event.getX();
eventY = event.getY();
invalidate();
break;我们先找到结束点,我们说了结束点是这个线段的中间位置,所以很容易求出它的坐标endX,endY;控制点是上一个手指位置即mPreX,mPreY;那有些同学可能会问了,那起始点是哪啊。在开篇讲quadTo()函数时,就已经说过,第一个起始点是Path.moveTo(x,y)定义的,其它部分,一个quadTo的终点,是下一个quadTo的起始点。
所以这里的起始点,就是上一个线段的中间点。所以,这样就与钢笔工具绘制过程完全对上了:把各个线段的中间点做为起始点和终点,把终点前一个手指位置做为控制点。
同样把lineTo和quadTo实现的S拿来对比下:
从效果图中可以明显可以看出,通过quadTo实现的曲线更顺滑
Ok啦,quadeTo的用法,到这里就结束了,下部分再来讲讲rQuadTo的用法及波浪动画效果
贝塞尔曲线实现水波纹效果
- Path.rQuadTo():
该函数声明如下:
public void rQuadTo(float dx1, float dy1, float dx2, float dy2)
其中:
- dx1:控制点X坐标,表示相对上一个终点X坐标的位移坐标,可为负值,正值表示相加,负值表示相减;
- dy1:控制点Y坐标,相对上一个终点Y坐标的位移坐标。同样可为负值,正值表示相加,负值表示相减;
- dx2:终点X坐标,同样是一个相对坐标,相对上一个终点X坐标的位移值,可为负值,正值表示相加,负值表示相减;
- dy2:终点Y坐标,同样是一个相对,相对上一个终点Y坐标的位移值。可为负值,正值表示相加,负值表示相减;
这四个参数都是传递的都是相对值,相对上一个终点的位移值。
比如,我们上一个终点坐标是(300,400)那么利用rQuadTo(100,-100,200,100);
得到的控制点坐标是(300+100,400-100)即(400,300)
同样,得到的终点坐标是(300+200,400+100)即(500,500)
所以下面这两段代码是等价的:
利用quadTo定义绝对坐标
path.moveTo(300,400);
path.quadTo(400,300,500,500); 与利用rQuadTo定义相对坐标
path.moveTo(300,400);
path.rQuadTo(100,-100,200,100)- 2、使用rQuadTo实现波浪线
在上篇中,我们使用quadTo实现了一个简单的波浪线:
各个点的计算我们上面已经计算过了,
下面我们将它转化为rQuadTo来重新实现下:
private void init() {
//初始化画笔
paint = new Paint();
paint.setTextSize(100);
paint.setColor(Color.RED);
paint.setStyle(Paint.Style.STROKE);
paint.setTextSize(100); //单位为 sp
paint.setStrokeWidth(5);
path = new Path();
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
path.moveTo(100,300);
path.rQuadTo(100,-100,200,0);
path.rQuadTo(100,100,200,0);
canvas.drawPath(path, paint);
}简单来讲,就是将原来的:
path.moveTo(100,300);
path.quadTo(200,200,300,300);
path.quadTo(400,400,500,300);
转化为:
path.moveTo(100,300);
path.rQuadTo(100,-100,200,0);
path.rQuadTo(100,100,200,0);
第一句:path.rQuadTo(100,-100,200,0);是建立在(100,300)这个点基础上来计算相对坐标的。
所以
控制点X坐标=上一个终点X坐标+控制点X位移 = 100+100=200;
控制点Y坐标=上一个终点Y坐标+控制点Y位移 = 300-100=200;
终点X坐标 = 上一个终点X坐标+终点X位移 = 100+200=300;
终点Y坐标 = 上一个终点Y坐标+控制点Y位移 = 300+0=300;
所以这句与path.quadTo(200,200,300,300);对等的第二句:path.rQuadTo(100,100,200,0);是建立在它的前一个终点即(300,300)的基础上来计算相对坐标的!
所以
控制点X坐标=上一个终点X坐标+控制点X位移 = 300+100=200;
控制点Y坐标=上一个终点Y坐标+控制点Y位移 = 300+100=200;
终点X坐标 = 上一个终点X坐标+终点X位移 = 300+200=500;
终点Y坐标 = 上一个终点Y坐标+控制点Y位移 = 300+0=300;
所以这句与path.quadTo(400,400,500,300);对等的
最终效果也是一样的。
通过这个例子,只想让大家明白一点:rQuadTo(float dx1, float dy1, float dx2, float dy2)中的位移坐标,都是以上一个终点位置为基准来做偏移的!
实现波浪效果
- 1、实现全屏波纹
上面我们已经能够实现一个波形,只要我们再多实现几个波形,就可以覆盖整个屏幕了。
对应代码如下:
public class CustomView extends View {
private Paint paint;
private Path path;
private int mItemWaveLength = 400;
private int originY = 300;
private int diffY = 100;
public CustomView(Context context) {
super(context);
init();
}
public CustomView(Context context, @Nullable AttributeSet attrs) {
super(context, attrs);
init();
}
public CustomView(Context context, @Nullable AttributeSet attrs, int defStyleAttr) {
super(context, attrs, defStyleAttr);
init();
}
private void init() {
//初始化画笔
paint = new Paint();
paint.setColor(Color.RED);
path = new Path();
paint.setStyle(Paint.Style.STROKE);
paint.setStrokeWidth(5);
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
path.reset();
path.moveTo(-mItemWaveLength, originY);
int halfWaveLen = mItemWaveLength / 2;
for (int i = -mItemWaveLength; i <= getWidth() + mItemWaveLength; i += mItemWaveLength) {
path.rQuadTo(halfWaveLen / 2, -diffY, halfWaveLen, 0);
path.rQuadTo(halfWaveLen / 2, diffY, halfWaveLen, 0);
}
path.lineTo(getWidth(), getHeight());
path.lineTo(0, getHeight());
path.close();
canvas.drawPath(path, paint);
}
}
最难的部分依然是在onDraw函数中:
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
path.reset();
path.moveTo(-mItemWaveLength, originY);
int halfWaveLen = mItemWaveLength / 2;
for (int i = -mItemWaveLength; i <= getWidth() + mItemWaveLength; i += mItemWaveLength) {
path.rQuadTo(halfWaveLen / 2, -diffY, halfWaveLen, 0);
path.rQuadTo(halfWaveLen / 2, diffY, halfWaveLen, 0);
}
canvas.drawPath(path, paint);
}我们将mPath的起始位置向左移一个波长(一个凹凸波属于一个波长):
mPath.moveTo(-mItemWaveLength,originY);
然后利用for循环画出当前屏幕中可能容得下的所有波:
for (int i = -mItemWaveLength; i <= getWidth() + mItemWaveLength; i += mItemWaveLength) { path.rQuadTo(halfWaveLen / 2, -diffY, halfWaveLen, 0); path.rQuadTo(halfWaveLen / 2, diffY, halfWaveLen, 0); }mPath.rQuadTo(halfWaveLen/2,-diffY,halfWaveLen,0);画的是一个波长中的前半个波,mPath.rQuadTo(halfWaveLen/2,diffY,halfWaveLen,0);画的是一个波长中的后半个波。大家在这里可以看到,屏幕左右都多画了一个波长的图形。这是为了波形移动做准备的。
到这里,我们是已经能画出来一整屏幕的波形了,下面我们把整体波形闭合起来。并改变画笔样式为填充
private void init() {
//初始化画笔
paint = new Paint();
paint.setColor(Color.RED);
path = new Path();
paint.setStyle(Paint.Style.FILL_AND_STROKE);
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
path.reset();
path.moveTo(-mItemWaveLength + dx, originY);
int halfWaveLen = mItemWaveLength / 2;
for (int i = -mItemWaveLength; i <= getWidth() + mItemWaveLength; i += mItemWaveLength) {
path.rQuadTo(halfWaveLen / 2, -diffY, halfWaveLen, 0);
path.rQuadTo(halfWaveLen / 2, diffY, halfWaveLen, 0);
}
path.lineTo(getWidth(), getHeight());
path.lineTo(0, getHeight());
path.close();
canvas.drawPath(path, paint);
}- 2、实现移动动画
让波纹动起来其实挺简单,利用调用在path.moveTo的时候,将起始点向右移动即可实现移动,而且只要我们移动一个波长的长度,波纹就会重合,就可以实现无限循环了。
为此我们定义一个动画:
public void startAnim(){
ValueAnimator animator = ValueAnimator.ofInt(0,mItemWaveLength);
animator.setDuration(2000);
animator.setRepeatCount(ValueAnimator.INFINITE);
animator.setInterpolator(new LinearInterpolator());
animator.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
@Override
public void onAnimationUpdate(ValueAnimator animation) {
dx = (int)animation.getAnimatedValue();
postInvalidate();
}
});
animator.start();
} 动画的长度为一个波长,将当前值保存在类的成员变量dx中;
然后在画图的时候,在path.moveTo()中加上现在的移动值dx:mPath.moveTo(-mItemWaveLength+dx,originY);
完整的绘图代码如下:
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
path.reset();
path.moveTo(-mItemWaveLength + dx, originY);
int halfWaveLen = mItemWaveLength / 2;
for (int i = -mItemWaveLength; i <= getWidth() + mItemWaveLength; i += mItemWaveLength) {
path.rQuadTo(halfWaveLen / 2, -diffY, halfWaveLen, 0);
path.rQuadTo(halfWaveLen / 2, diffY, halfWaveLen, 0);
}
path.lineTo(getWidth(), getHeight());
path.lineTo(0, getHeight());
path.close();
canvas.drawPath(path, paint);
}
如果把波长设置为1000,就可以实现本段开篇的动画了。
如果想让波纹像开篇时那要同时向下移动,大家只需要在path.moveTo(x,y)的时候,通过同时移动y坐标就可以了
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
path.reset();
path.moveTo(-mItemWaveLength + dx, originY + dy);
int halfWaveLen = mItemWaveLength / 2;
for (int i = -mItemWaveLength; i <= getWidth() + mItemWaveLength; i += mItemWaveLength) {
path.rQuadTo(halfWaveLen / 2, -diffY, halfWaveLen, 0);
path.rQuadTo(halfWaveLen / 2, diffY, halfWaveLen, 0);
}
path.lineTo(getWidth(), getHeight());
path.lineTo(0, getHeight());
path.close();
canvas.drawPath(path, paint);
//dy控制波纹向下移动
dy++;
if (dy >= getHeight() - originY + diffY){
mHanimator.cancel();
}
}最终效果图如下: