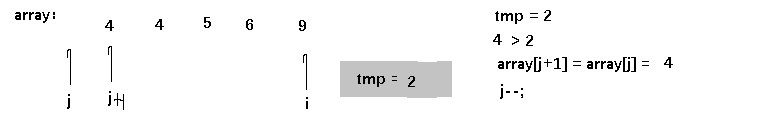常见的6种排序图解 - java语言描述

目录

1、冒泡排序

2、直接插入排序

3. 希尔排序

4、归并排序

5. 快速排序

6. 选择排序

首先，在说几个排序算法之前，先自己写一个简单的工具类，判断一个数列是否有序（以升序为例），如果不是升序的数列，在出现乱序的地方把附近的两个元素输出一下：

 /**
     * 判断一组数据是不是升序
     * @param array  传入一个需要判断是否有序的数列
     */
    public static void isSortedAsc(int[] array)
    {
        for (int i=1; i

运行结果如下：

以下的排序都以升序为例......

在写一个主方法，用来测试排序的结果：

public static void main(String[] args) {
        // 随机生成10000个数 对他们进行排序
        int[] array = new int[10000];
        Random random = new Random();
        for (int i = 0; i < array.length; i++) {
            array[i] = random.nextInt(10000)+1;
        }
        System.out.println("排序前：" + Arrays.toString(array));
        // 记录时间
        long start = System.currentTimeMillis();
        // 这里调用具体的排序方法
        sort(array);
        long end = System.currentTimeMillis();
        System.out.println("运行时间:"+(end-start));
        System.out.println("排序后："+Arrays.toString(array));
        SortUtils.isSortedAsc(array);
    }

1、冒泡排序

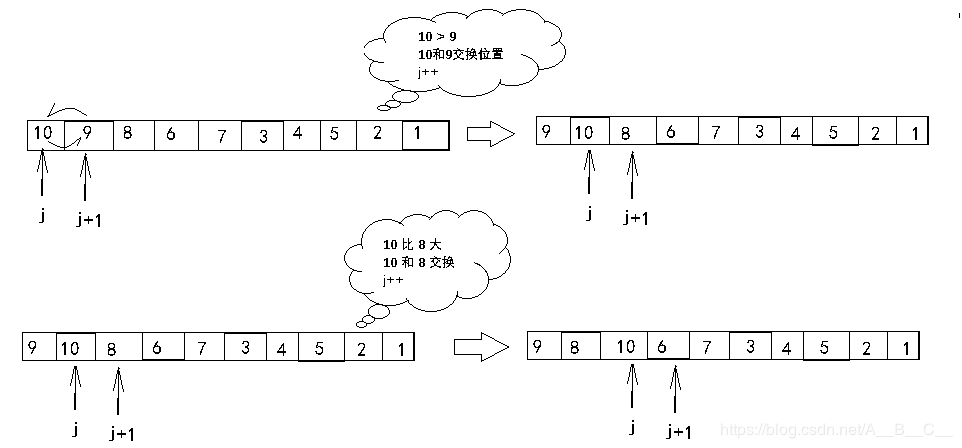
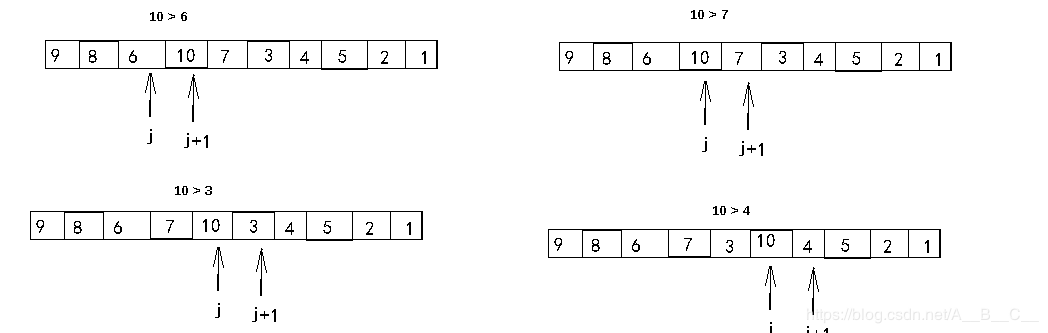
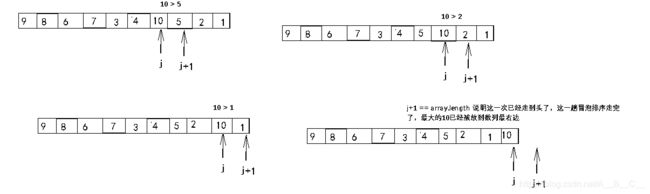
冒泡排序是几种排序算法中最常见的一种，其思想就是：给定一组数据，然后按顺序两两数字进行比较，如果前面的一个元素比后面的大，就让他们两个进行交换，然后继续朝后比较，从数列最左边走到数列最右边的过程称为一趟冒泡排序，经过一趟冒泡排序，会把最大的元素放到数列的最右边。如下图

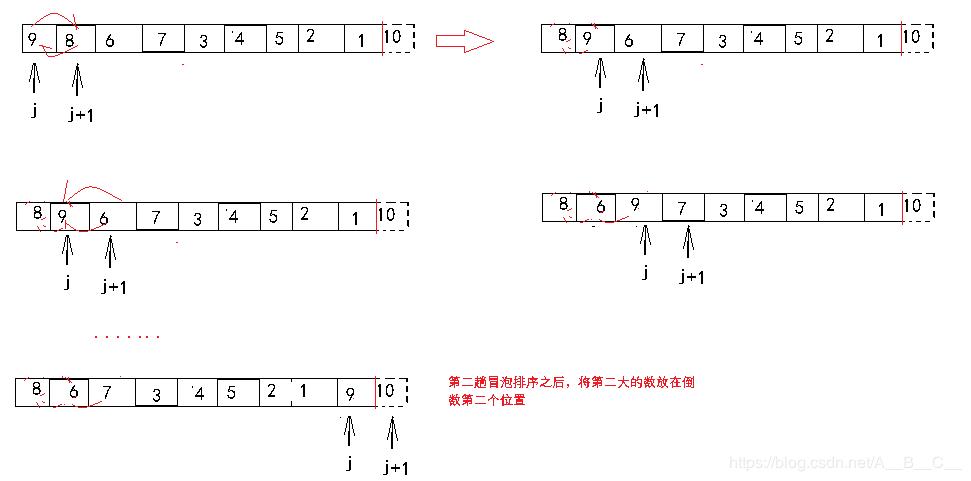
当一趟冒泡排序走完之后，最大的数就放到了最右边，然后现在我们就可以直接对剩下的9个数再进行冒泡排序：

当这一趟冒泡排序结束之后，第二大的数就会被挪到倒数第二个位置，如下图：

通过以上分析，冒泡排序代码如下：

public static void bubbleSort(int[] array){
        // 外层循环表示的是变量j一共要进行多少趟冒泡排序
        for (int i=0; i array[j+1])
                {
                    int tmp = array[j];
                    array[j] = array[j+1];
                    array[j+1] = tmp;
                    // 每趟排序之后又数据交换，就说明数组还不是有序的，就把标志设置为假
                    flag = false;
                }
            }
            if (flag) {
                // 如果其中某一趟排序的时候发现没有一个数据交换，就说明数组已经有序了，就不用再进行排序了，可以直接退出循环
                break;
            }
        }
    }

使用上面的两个测试类进行测试：

冒泡排序分析：

• 时间复杂度：O(n^2)
• 空间复杂度：O(1)
• 稳定性 ：稳定

2、直接插入排序

思想：两个下标 i， j，一个临时变量tmp，i用来遍历待排序序列，tmp存放arr[i]，j=i-1，j朝0的方向递减，将tmp中的值插入合适的位置。直接插入排序的思想就和我们打扑克牌的情况一样，当我们拿到第一张牌的时候，由于此时手上只有一张牌，所以它一定是最小（或最大）的一张，当我们接到第二张牌的时候，如果它比第一张牌小，我们就把它放第一张牌的前边，反之，就放到它后边，以此类推。现在给我们一个数组，我们就默认它第一个元素一定是有序的，从第二个元素开始，如果第二个元素比第一个大，就不用管他，如果第二个元素小于第一个元素，就把第二个元素放第一个前面去，这时前两个元素就有序了；然后到了第三个元素，如果第三个元素大于第二个元素，那么第三个元素一定大于第一个元素，也就不用管它，如果它比第二个元素小，就把第二个元素挪到第三个元素的位置，然后第三个和第一个在比较，如果第三个元素大于第一个，就把它放第一个后面（第二个的位置），如果第三个小于第一个，就把它放第一个前面，以此类推，过程如下图：

图解： 这里我们定义一个临时变量tmp存储当前元素

代码：

public static void insertSort(int[] array){
        // 从第二个元素开始 一次朝后走
        for(int i=1; i=0 && array[j] > tmp )
            {
                array[j+1] = array[j];
                j--;
            }
            array[j+1] = tmp;
        }
    }

测试结果：

直接插入排序总结：

• 时间复杂度：O(n)
• 空间复杂度：O(1)
• 稳定性 ：稳定
• 适用场景：适合用来排一些接近有序的数列，因为如果数列有序，直接从左到右走一遍就行了，时间复杂度为O(n)，但是如果乱序或倒序，每走一步，它都会在往回走，把当前元素插入到合适的位置在往后走。

3.希尔排序

思想：希尔排序是对直接插入排序的一种优化；采用的是将数据分组，然后每组在组内进行直接插入排序

为什么要分组呢：试想一下加入现在有10000个数据要进行直接插入排序，时间复杂度为 10000 * 10000 = 10000 0000 ；但是如果将这组数据分成100组 ， 每组进行插入排序，时间复杂度就变成了 100 * 100 * 100 = 1 00 00 00 。直接少了两个0 ......

那么要怎么分组呢：如果是让我们这种普通人来分组，就下面这组数据，要平均分为两种，我们一开始想到的肯定是这样

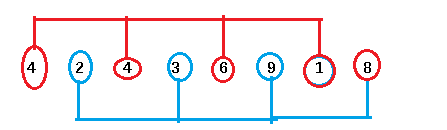
但是人家科学家分组就不一样了，他们分组是这么分的：

那么这么分组有什么好处呢：加入我们对下面这组数据每组的组内进行直接插入排序：

组内排序之后，我们会发现，每一组在组内都是有序的，也就是说，每一组的左边的数据都比较小，右边的数据都比较大，整体也是一样，这样的话我们就可以认为整个数组是接近有序的，上面已经说过，直接插入排序适合用来排接近有序的数列，所以现在在对整体进行直接插入排序就会快很多。

所以希尔排序的本质还是直接插入排序。

代码：

public static void shellSort(int[] array, int gap) {
        // i从gap的位置开始
        for (int i=gap; i=0 && array[j] > tmp)
            {
                array[j+gap] = array[j];
                j -= gap;
            }
            array[j+gap] = tmp;
        }
    }

希尔排序分析：

• 时间复杂度：O(n^1.3 - n^1.5)
• 空间复杂度：O(1)
• 稳定性：不稳定

4、归并排序

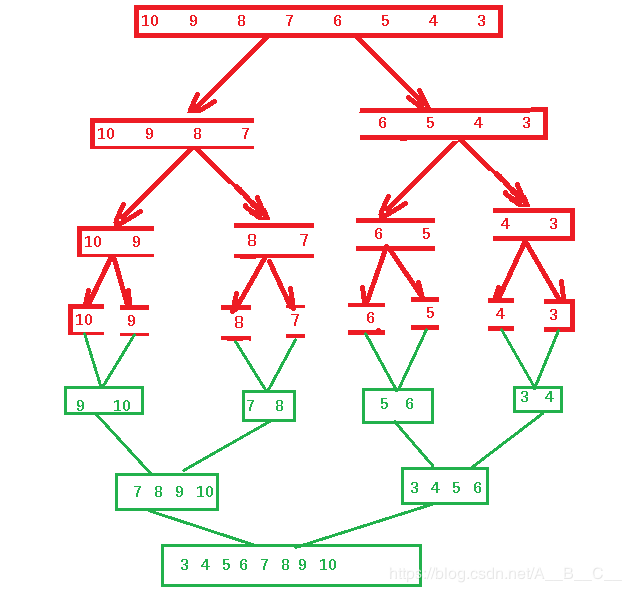
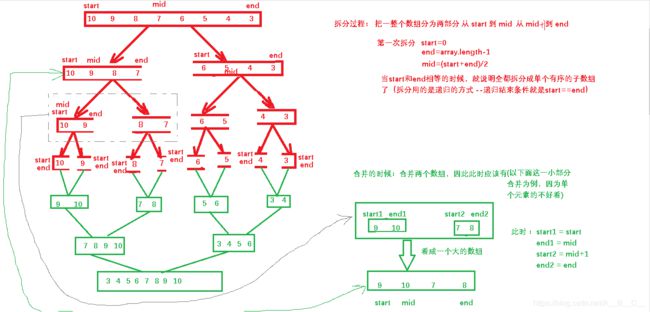
思想：归并排序的思想同样是将一个大的数列划分成单个有序的数据（之后一个元素的数列一定是有序的），然后在把有序的小数列合并成一个大的有序数列，从而实现整体有序的结果，过程如下图：

代码：

private static void mergeSort(int[] array, int start, int end) {
        int mid = (start+end)/2 ;
        if (end == start)
        {
           return ;
        }
        // 朝左边拆分
        mergeSort(array, start, mid);
        // 朝右边拆分
        mergeSort(array, mid+1, end);
        // 拆分成单个的之后，归并
        merge(array, start, mid, end);
    }

    private static void merge(int[] array, int start, int mid, int end) {
        int[] tmpArray = new int[array.length] ;
        int i = start ; // 保留一个start的值，最后拷贝数组的时候使用
        int start1 = start; 
        int end1 = mid;
        int start2 = mid+1;
        int end2 = end;
        while (start1 <= end1 && start2 <= end2)
        {
            // 哪一个数组中的值小把哪一个的值拿到新数组中
            if (array[start1] <= array[start2]){
                tmpArray[start++] = array[start1++];
            }else {
                tmpArray[start++] = array[start2++];
            }
        }
        // 如果第一个数组还没有走完
        while (start1 <= end1)
        {
            tmpArray[start++] = array[start1++];
        }
        // 如果第二个数组还没有走完
        while (start2 <= end2)
        {
            tmpArray[start++] = array[start2++];
        }
        // 数组拷贝
        for ( ; i<=end; i++)
        {
            array[i] = tmpArray[i];
        }
    }

运行结果：

优化：

但是这么写仔细观察会发现有一点问题，因为每次递归都会创建一个和array一样大的数组，但是只用了其中的一小部分，所以可以将tmpArray在排序之前只创建一次，然后作为参数传递就可以了，不需要在递归中创建。

private static void mergeSort_R(int[] array, int start, int end, int[] tmpArr)
    {
        if (start < end)
        {
            int mid = (start+end)/2 ;
            mergeSort_R(array, start, mid, tmpArr);
            mergeSort_R(array, mid+1, end, tmpArr);
            merge(array, start, mid, end, tmpArr);
        }
    }

    private static void merge(int[] array, int start, int mid, int end, int[] tmpArr) {
        int pos = start;
        int index = start;
        int start2 = mid+1 ;
        while (start <= mid && start2 <= end){
            if (array[start] < array[start2]) {
                tmpArr[index++] = array[start++];
            }else {
                tmpArr[index++] = array[start2++];
            }
        }
        while (start <= mid){
            tmpArr[index++] = array[start++];
        }
        while (start2 <= end){
            tmpArr[index++] = array[start2++];
        }
        // 数组拷贝
        for(int i=pos; i<=end; i++)
        {
            array[i] = tmpArr[i];
        }
    }

 

5. 快速排序

思想：和上面那种归并排序的思想类似，都是将一个大的问题划分为多个小问题，快速排序是 ：先选取一个基准值，每经过一趟冒泡排序，就可以将比基准大的放在基准值的右边，比它小的放它左边。然后在分别对基准值左边的和基准值右边的分别进行冒泡排序。直到整个数列有序。

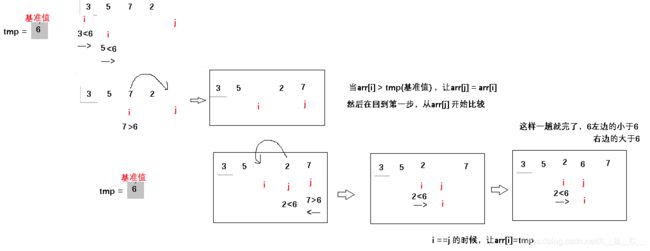
那么现在主要的问题就是怎么将一个数组根据基准值分为两部分，使左边的小于基准值，右边的大于基准值。通常的方法是挖坑法

下面，再结合代码看一下这个 ‘挖坑’ 的过程：

 private static int partion(int[] arr, int left, int right)
    {
        // 保存第一个位置的元素
        int tmp = arr[left];
        while (left != right)
        {
            // 右边的和tmp比较 如果右边的比tmp大，就不用管，继续朝左边走 
            // 注意这里得有等号，不然如果左边等于tmp，右边等于tmp，会出现死循环，下面等号也是一样
            while (left != right && arr[right] >= tmp)
            {
                right--;
            }
            // 如果右边的数小于tmp，就把右边的数赋给左边的数
            arr[left] = arr[right];
            // 左边的数和tmp比较，如果左边的数大于tmp 就把左边的数赋值给右边的数
            while (left != right && arr[left] <= tmp){
                left++ ;
            }
            arr[right]= arr[left];
        }
        // 当left == right 把tmp的值赋给当前位置
        arr[left] = tmp;
        // 返回位置下标
        return left;
    }

最后通过递归的方式，让返回位置的左边也进行快速排序，右边也进行快速排序：

public static void quickSort (int[] arr, int left, int rigth){
        // 获取关键字的位置
        int mid = partion(arr, left, rigth);
        // 如果关键字左边还剩一个元素，就不用比了
        if (mid-left > 1){
            quickSort(arr, left, mid-1);
        }
        // 如果右边还剩一个元素，也就不用比了
        if (rigth-mid > 1){
            quickSort(arr, mid+1, rigth);
        }
    }

结果测试：

快排优化1 --- 三数取中法

但是这样的快排还是有一些问题，假如每次排序数列第一个刚好是最大的或最小的，就会使快速排序时间复杂度退化为O(n^2)，因此需要对这个快速排序进行优化，常见的优化方式有：随机取基法，三数取中法

• 随机取基法：就是随机取一个数作为基数，这样就可以避免取到最大或最小的数作为基数，但是由于是随机的，所以这种方法完全是一种看人品的方法，所以不推荐使用
• 三数取中法：就是在第一个数，中间位置的数，最后位置的数 ，在这三个数中，取这三个数（按大小排序）的中间值作为基准值，然后在进行快速排序，这样可以保证至少每次取得基准值都不会是最大或最小的一个数，下面具体说说这种方法：

至于三数取中的实现，就有很多方式了，因为只是对3个数的比较，可以使用if语句比较大小然后交换值，也可以将这三个数排序然后按顺序赋值等方法：

/**
     * 快排优化1
     *     三数取中法 : 最后要达到的效果：array[mid] < array[low] 

然后在每次要进行快排的操作时，都调用一下三数取中的方法即可；

快排优化2 ：使用插入排序

当使用快排对数列进行排序时，排到一定程度数据就接近有序了，此时可以不必在使用递归的快排，而使用插入排序对数列进行排序：

public static void sort(int[] array, int start, int end){
        // 优化方式1：先用三数取中法
        medianOfThree(array, start, end);

        // 优化方式2：当一个区间中剩余数的个数小于等于16的时候，我们就认为这个区间的数已经接近有序了，次数可以使用插入排序接着排
        if (end-start+1 <= 16) // end-start+1 表示start到end之间的元素个数
        {
            insertSort(array, start, end);
        }
        int par = partion(array, start, end);
        // 递归左边  左边还剩一个元素就不用排序了
        if (par > start+1) {
            sort(array, start, par-1);
        }
        if (par < end-1){
            sort(array, par+1, end);
        }
    }

最后的运行结果：

6. 选择排序

思想：选择排序就是先选择最小的一个数，和第一个数交换，然后在选择第二小的数，和第二个位置的数交换，以此类推...

代码实现：

 public static void selectSort(int[] array)
    {
        // 把倒数第二大的数放在倒数第二个位置的时候，最大的数一定在最后的位置，就不用在朝后比较了
        for (int i=0; i array[j]){
                    int tmp = array[i];
                    array[i] = array[j];
                    array[j] = tmp;
                }
            }
        }
    }

测试结果：