关于《算法》上的红黑树的理解和简单实现(C代码)
关于红黑树的资料网上有很多,写这篇博客主要是记录一下自己的一些理解,也提供给大家参考。本文参考Sedgewick的《算法》所写,主要是2-3查找树到红黑树的过渡,有误的地方请大家指出。
关于红黑树的定义,《算法》和《算法导论》有些不同,这篇文章的理解和实现是针对《算法》中的定义的,如果需要看《算法导论》的实现的朋友可以参考其它资料。《算法导论》对红黑树的描述大概是这样的:
(1)每个结点或是红色,或是黑色。
(2)根结点是黑色。
(3)每个叶子结点是黑色。
(4)如果有一个结点是红色,则它的两个儿子都是黑色。
(5)对每个结点,从该结点到其孙子结点的所有路径上包含相同数目的黑色结点。
《算法》上给出的另外一种等价的定义是这样的:(1)红链接均为左链接
(2)没有任何一个结点同时和两条红链接相连
(3)该树是完美黑色平衡的,即任意空链接到根结点的路径上的黑链接数量相同
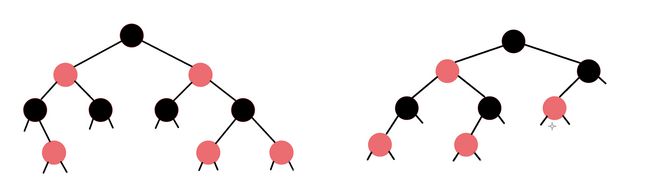
先贴一副图让大家有个印象: 首先红黑树是平衡树的一种,但是它并不是完美平衡的(左右子树高度差最多为1,我们看右边的图可以知道),要实现一棵完美平衡树的操作要更多一些,而红黑树降低了对平衡的要求来换取更简单的操作,让插入和删除的性能更好一些。红黑树要实现的是树的黑色完美平衡,也就是上面定义的第5和第3点,意思是我们不看红色结点,剩下的就是完美平衡的了,或者说,从根开始,到每个叶子结点所经过的黑色链接数是相同的(可以数一下,上面两幅图都是3),这可以保证一棵大小是N的红黑树高度不超过2LgN(最坏的情况就是有一支是红黑红黑...),所以对每个节点的搜索都可以在LgN时间内完成。
我们来看一下两种定义的区别,《算法》的定义进一步要求红链接都是左链接,这里解释一下。我们稍后就会看到,旋转操作并不会影响整棵树的结构,一个红链接是左链接还是右链接其实没有关系,因为红黑树要维护的是黑色完美平衡,右链接通过左旋就可以变成左链接,所以这两个定义其实是等价的。《算法》上这样定义的原因,是让红黑树和2-3树对应起来,让操作更统一,我们更容易理解(要调整的情况会少一些,但是性能上可能没那么好吧)。OK,对红黑树有了直观的印象之后,我们来看看它是怎么实现黑色完美平衡的,按照套路,我们先了解一下2-3树。
2-3查找树
2-3树是最简单的B-树,完整的定义是这样子的:
2-3查找树:一棵2-3查找树或为一棵空树,或由以下结点组成:
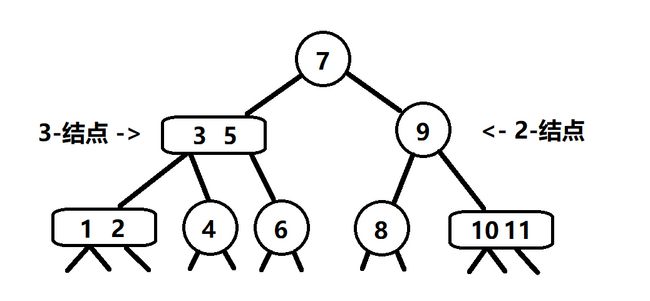
- 2-结点,含有一个键(及其对应的值)和两条链接,左链接指向的2-3树中的键都小于该结点,右链接指向的2-3树中的键都大 于该结点
- 3-结点,含有两个键(及其对应的值)和三条链接,左链接指向的2-3树中的键都小于该结点,中链接指向的2-3树中的键都位于该结点的两个键之间,右链接指向的2-3树中的键都大于该结点
还是看图更加直观(ps:这篇文章关于树的结点的图示都只画出了键,键用数字表示不代表键只能是数字):结合定义可以知道,2结点就是普通的二叉树结点,3节点就是在2结点里面增加一个键,让它有3棵子树而已,当然,每棵子树都要满足大小关系,最左边的最小,中间的在中间,最右边的最大(3-结点画得这么丑是有原因的)。这里一定要指出,不是每一棵2-3树都是完美平衡的(这很正常,只是图示正好是完美平衡而已),这里介绍一种自底向上的构建方法,我们来看看要创建一棵完美平衡的2-3树的过程中会遇到什么问题:
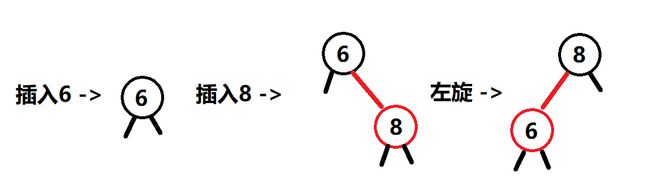
首先我们插入6,再插入8,这里我们遇到第一个选择,我们可以把8插入到6的子树中,也可以把8作为第二个键。这里我们的方法是把它放在第二个键的位置,让它成为一个3-结点:
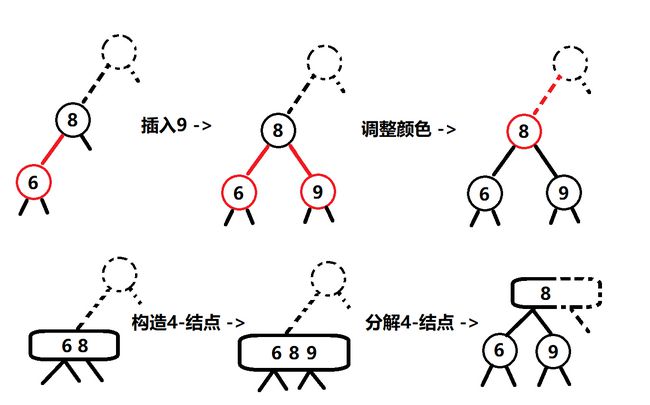
继续插入7,这里是第二个选择,我们可以把它插入到这个3-结点的任何一个子树中,这样的话就是自顶向下生长的,而我们的自底向上的方法比较特别,我们先去构造一个4-结点,然后再把这个结点分解成3个2-结点,我们规定中间的子树跟随左边的结点(其实都可以,这就是我画成这么丑的原因之一):
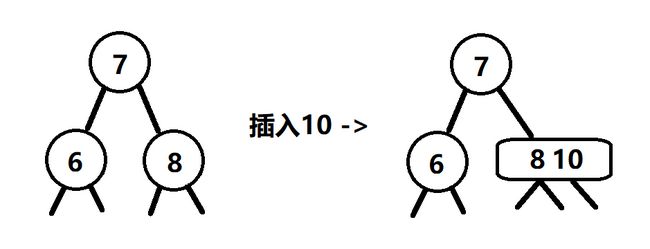
继续插入10,由于我们是自底向上生长的,所以当然得插入到最低的一层,也就是8的这个结点而不是7的旁边,同样我们得放到8的旁边,让它成为一个3-结点,而不是插入到它的子树中:
继续插入9,按照上面的方式,将8,10这个3-结点分解成3个2-结点,于是9很自然的跑到了7的旁边,这里要注意区别,并不是将9直接放在7的旁边:
这里我们得出规律来,我们构造完美平衡的2-3树的方法很简单,首先从上往下搜索,找到你要插入的结点应该要插入的位置,当然这个位置是最低一层的,然后从下往上,将含有的4-结点分解掉,继续插入4和5看看是不是这样子的:
继续插入1,3,11,2 就可以得到最开始的图示的树,这里应该是比较容易理解的。我们再来观察一下这样的构造方法,在我们插入的过程中,每一步都是从最低层开始,在往上分解4-结点的过程中都没有改变树的结构,这就保证了树是完美平衡的,在搜索路径上要经过的结点(2-结点和3-结点)不会超过LgN个,准确来讲,一棵N个结点的完美平衡的2-3树的高度在Log(3,N)到LgN之间。当然了,要实现2-3树是比较复杂的,尤其是我们还要考虑到删除结点的情况,一个完全等价的而在实现上更为简单的办法就是红黑树。
2-3查找树与红黑树的对应
要实现2-3树的一个很麻烦的地方在于,它的结点有两种,维护起来非常的不方便,红黑树的做法是将这两种结点统一成一种,而用一个颜色位来区分,我们来看看红黑树怎么表示3-结点(这是把3-结点画这么丑的另外一个原因):
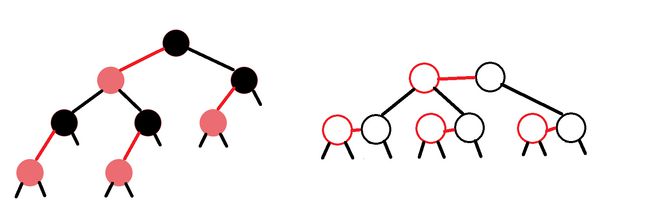
很简单,用一个红色结点和上层的一个黑色结点联合起来就可以表示一个3-结点,而2-结点就是普通的黑色结点,这样就把两种结点统一起来了。我们可以回过头来看,为什么红黑树只维护黑色完美平衡,这是因为一个红色结点实际上是和上层的黑色结点在一起的,我们把红黑树铺平,就可以很直观的看出它和2-3树的对应关系了(这种对应关系是在《算法》的定义下的,如果在《算法导论》的定义下会有冲突,但也可以通过旋转还原,顺便接受一下这样的画风):
上面这个图是最开始的一张图,把它铺平就容易看出它的根结点到叶子结点的黑色路径是3了,这里要说明一下颜色的表示方法,因为红色结点要与上层的黑色结点相连,所以相连接的这条线是红链接,也就是说,一个结点的颜色,就是这个结点与父亲结点的链接颜色(也很正常,用子树的链接也确定不了因为有2个)。
现在再看回定义,为什么不可能有一个结点同时有两条红链接呢?对了因为两条红链接相连就变成了一个4-结点了,那为什么一个红色结点的子结点都是黑色呢?同样是这个原因了。另外,我们看图也可以知道,规定红链接是左链接还是右链接是没有关系的,都是一个3-结点而已,他们是等价的,那怎样通过变换可以把左右链接进行转换呢,下面再解释一下什么是旋转操作。
旋转操作其实很简单,要知道旋转是针对链接的(黑链接也可以旋转,不过对我们构造树没有帮助),将一个右链接转成一个左链接就是左旋,将一个左链接转成一个右链接就是右旋,不用多说,只要处理好子树的关系就没问题了:
我们可以观察到,旋转操作不会改变树的结构,充其量是镜像了一下,这再次证明最开始的两种定义确实是等价的,我们马上就可以看到,通过这两种简单的操作就可以处理好构建红黑树的调整工作了。
红黑树的插入及其简单实现
这次我们用的方法和2-3树的一样,自底向上,先找到要插入的位置,插入,重新调整树的结构这么个套路,我们也来看看在插入的过程中会遇到什么问题。由于2-3树会优先让结点成为3-结点,那我们就统一,在插入的时候总是插入红色结点(总是插入黑色结点也不是个办法),这里就遇到了第一个问题,如果这个结点在右边怎么办,也就是说现在有了一个红链接是右链接,oh那我们就左旋让它变成左链接:
这里还要说明一点,红黑树规定根结点是黑色的,所以在调整完成后还有一步把根结点变成黑色的操作。我们继续插入9,这时8这个结点的两个子结点都是红色的,我们对应2-3树,发现这是个4-结点(这个时候树高还是1),所以我们得把它分解成3个2-结点,在红黑树里这个操作就很简单了,把子树都变成黑色就可以了(这个时候树高就是2了),然后我们把这个结点变成红色,这是因为这个结点要是要和父结点结合成为3-结点的:
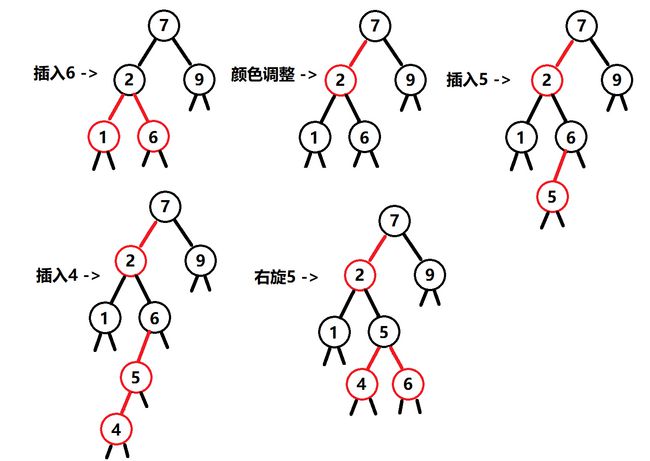
那又要问了,如果不插入9,我们插入5或者7,这样不就有两个连续的红链接了吗,哦是的,但是这也是一个4-结点呀,我们可以把上面的红链接右旋下来,再改换颜色就好了:
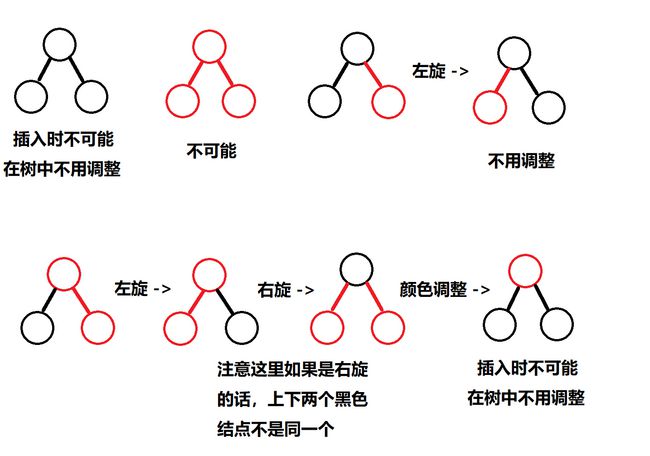
插入7已经是调整工作里面最复杂的了,在一开始的8结点不可能是红链接,不然在插入7之前就已经有2条连续的红链接了,所以调整以后的红色结点7就不用考虑再换颜色的问题了。调整的工作其实就是用前面的3种方法,左旋,右旋和调整颜色,我们要调整的对象也就只是3个结点而已,我们列出所有的8种情况来看看(2x2x2):
仔细观察就可以知道,我们只要依次判断需不需要左旋,需不需要右旋,需不需要调整颜色就可以了,其他的情况都包含在里面了,OK套路就是这么简单,下面我们来简单的实现一下,调整的过程用递归来做会更加清晰,这里也不写键-值对了,用一个int作为结点的key,首先是数据结构(不要吐槽我的起名和c语言没有bool的问题):
struct Node
{
int key;
bool color;
Node *left;
Node *right;
};
#define BLACK false;
#define RED true;// 左旋操作
Node* rotateLeft(Node *p)
{
Node *temp = p->right;
p->right = temp->left;
temp->left = p;
temp->color = p->color;
p->color = RED;
return temp;
}
// 右旋操作
Node* rotateRight(Node *p)
{
Node *temp = p->left;
p->left = temp->right;
temp->right = p;
temp->color = p->color;
p->color = RED;
return temp;
}
// 颜色调整
void flipcolor(Node *p)
{
p->color = RED;
p->left->color = BLACK;
p->right->color = BLACK;
}// 创建一个含有key的新结点,返回该结点的指针
Node* createNode(int elem)
{
Node *p = (Node*)malloc(sizeof(Node));
p->key = elem;
p->left = nullptr;
p->right = nullptr;
p->color = RED;
return p;
}
// 判断当前结点是否为红色
bool isRed(Node*p)
{
if (p == nullptr) {
return false; // 叶子结点为黑色
}
return p->color == RED;
}Node* addNode(Node *root, int elem)
{
root = insertNode(root, elem); // 递归实现插入
root->color = BLACK; // 保证根节点一定是黑色
return root;
}
Node* insertNode(Node* p, int elem)
{
if (p == nullptr) {
return createNode(elem);
}
// 递归找到要插入的位置,相等的key则不进行任何操作
// 注意找到位置后并不是马上return,要回溯调整树的结构
if (elem > p->key) {
p->right = insertNode(p->right, elem);
}
else if (elem < p->key) {
p->left = insertNode(p->left, elem);
}
// 依次判断需不需要调整
if (isRed(p->right) && !isRed(p->left)) {
p = rotateLeft(p);
}
if (isRed(p->left) && isRed(p->left->left)) {
p = rotateRight(p);
}
if (isRed(p->left) && isRed(p->right)) {
flipcolor(p);
}
return p;
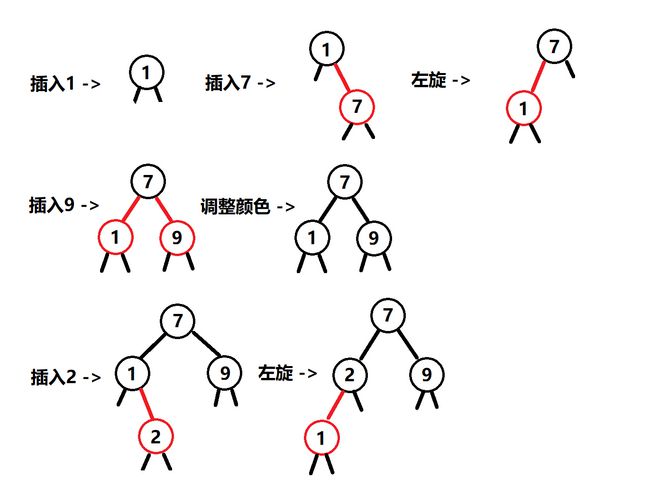
}上面这棵树不就又变成了一棵完美平衡树了吗,其实这棵树早就见过了,就是最开始的2-3树的例子,只是key不同罢了,这里面包含所有红黑树插入要调整的情况了,有兴趣的朋友也可以尝试将它变成非递归的版本。
写到这里似乎有点长,关于红黑树的删除下一篇再写吧。