Stanford公开课《编译原理》学习笔记(1~4课)

【摘要】 编译原理基础

示例代码托管在：http://www.github.com/dashnowords/blogs

B站地址：【编译原理】

Stanford公开课：【Stanford大学公开课官网】

课程里涉及到的内容讲的还是很清楚的，但个别地方有点脱节，任何看不懂卡住的地方，请自行查阅经典著作《Compilers——priciples, Techniques and Tools》(也就是大名鼎鼎的龙书）的对应章节。

一. 编译的基本流程

完整的编译的5个基本步骤包括lexcical anlysis,parse,sematic,optimize,code generate。课程中并没有使用复杂的编程语言，而是一种用于课堂教学的自发明语言COOL，很明显老师为它写好了编译器程序。

二. Lexical Analysis(词法分析阶段)

任务：将字符串分解成为[Type, (Value)]元组的形式的词法单元。

“龙书”里的示例更为直观，例如表达式语句 E = M * C ** 2进行词法分析后会得到如下的类似结果：

[id,指向符号表中E的条目的指针]

[assign_op]

[id,指向符号表中M的条目的指针]

[mult_op]

[id,指向符号表中C的条目的指针]

[exp_op]

[number,整数值2]

词法分析基本需要经历如下几个阶段：

Lexical Specification——>Regular expressions——>NFA——>DFA——>Table-driven Implementation of DFA

2.1 Lexical Specification(分词原则)

COOL中的基本Type包括如下几个类别：

• Indentifier标识符-指以字母开头后续为若干个字母或数字的字符组

• Integer-指一组非空的数字字符

• Keyword- 指语言中的关键词，例如if，else等

• Whitespace- 指一组非空的空格字符或换行符或制表符

很多程序设计语言中的分词原则基本都会覆盖关键字，运算符，标识符，常量，标点符号，他们也会在后面的实现中被作为终止符集合，课程板书中也提供了COOL分词原则的类正则形式。

分词时类型的正则匹配默认为贪婪模式，即匹配更多的字符。词法单元也具备一定的优先级次序（通常也是代码逻辑的实现顺序），例如if从正则上来判断既符合Keywords也符合Identifier，此时该单元的类型就应该标记为Keywords。这个阶段就完成了从Lecical Specification——>Regular expressions的部分。

2.2 Finite Automata (典型分词算法-有穷自动机)

FA是一个可以自动识别词法单元的机器，它是一个状态转换图，“有限”是指它包含的状态是有限的，一个状态读入一个字符后，后继的状态可能为：

• 后继状态为自身

• 后继状态只有一个

• 后继状态有多个

如果每次转换后的后继状态都是唯一的，则称为DFA（确定有限自动机），如果后继状态可能有多个则称为NFA（不确定有限状态机）。由于DFA的状态转移路径是唯一的，所以作为状态查询图时，无论成功或者失败只需要运行一次，但NFA就可能需要运行多次。

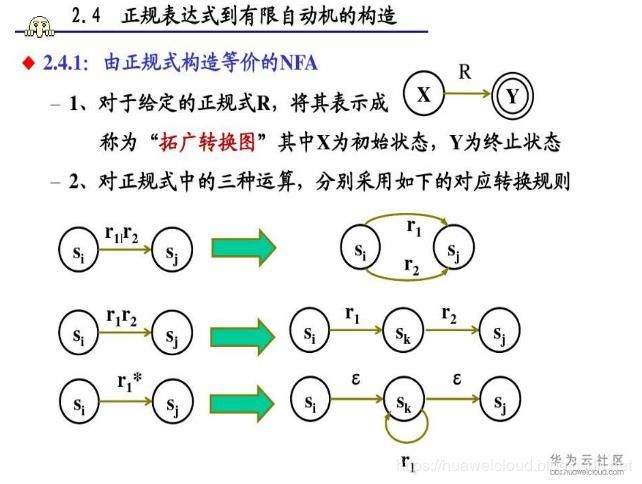
正则表达式是可以转换为NFA形式的，或许你已经在一些可视化正则表达式的网站上[https://regexper.com ]见过类似的形式。下图比较清晰地展示了从正则表达式到NFA状态图的转换规则(Regular expressions——>NFA)：

如果一个DFA和一个NFA能够识别的字符集是一致的，则称它们为等价的，对于任意NFA，一定存在一个DFA与其等价，由NFA构建DFA的过程被称为DFA的确定化，也就是NFA——>DFA的过程。这个过程是围绕ε -closure状态集合的概念展开的，大致的过程就是从起点开始，每次将当前状态和通过若干次ε转换（它是一个特殊的状态转移函数，表示转换后的状态还是当前状态）作为一个新的ε -closure状态集合 ，使用矩阵记录每个ε -closure集合转换前后的集合，最后对整个状态转移矩阵进行标记重命名，就可以得到一个DFA，事实上转化后的DFA中的每一个状态，就是NFA中的一个ε -closure集合，你可以将它理解成一个通过分组来简化表达方式的过程，相关的过程可以参考下面这个文章西北农林科技大学编译原理课程PPT【词法分析】，里面图比较多，能够辅助理解，本文不再赘述。

三. 手动实现分词器

至此1-4课就结束了，估计看视频课程的人也是一脸懵逼，因为课程并没有讲解如何利用DFA得到最终期望的形式——Token元组，那么最后我们就自己手动来实现一下。

3.1 基本定义

假设我们需要对下面这段代码进行分词解析：

let snippet = `
var b3 = 2;
a = 1 + ( b3 + 4);
return a;
`;

那么先来进行一些基本类型集合定义：

//解析结束标记
const EOF = undefined;

//Token Type 可识别的Token类型，
const TT = {
   num: 'num',
   id: 'id',
   keywords: 'keywords', //var | return
   lparen: 'lparen',// (
   rparen: 'rparen',// )
   semicolon: 'semicolon', //;
   whitespace: 'whitespace', // \n | \t | \s  (空格，制表符，换行符)
   plus: 'plus', // +
   assign: 'assign',// =
}

// 状态集类型，除开始和结束外，其他可以与Token支持的类型相对应，每次分词从start状态开始，接收一个字符后改变状态，直到在done状态结束时，可以得到一个token
const S = {
   start: 'start',
   done: 'done',
   ...TT
}

进行工具函数定义：

//判断是否为关键词(为简化流程，仅检测上面示例中包含的关键词)
const isKeywords = (token) => ['function', 'return', 'if', 'var'].includes(token);

//判断是否为数字
const isDigit = c => /\d/.test(c);

//判断是否为合法的标识符字符
const isValidId = c => /[A-Za-z0-9]/.test(c);

//判断是否为空格
const isBlank = c => /(\s|\t|\n)/.test(c);

3.2 构建DFA

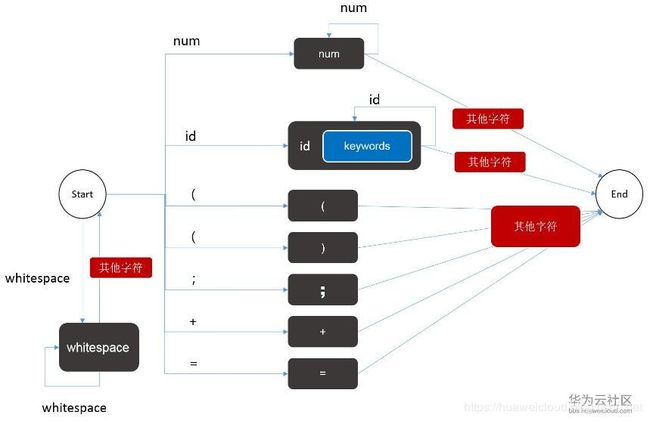
以上面定义的状态集合和token类别为依据构建DFA:

3.3 开始分词

分词的逻辑实际上就是，每次先将状态置为start,然后读入一个字符，根据该字符判断下一个状态，只要没有到达完成状态done就继续读入字符，每次到达done状态时，就可以得到一个token，将其记录下来，然后重新将状态置为start，开始寻找下一个token直到分析完整个代码段。也就是说DFA状态机每运行一轮，就得到一个token。参考代码如下：

/**
* 词法分析
*/
function tokenize(code) {
   let state = S.start;
   let currentToken;//标记当前寻找到的token
   let index = 0;//起始指针,每次分析指向start状态
   let lookup = 0;//前探指针,每次分析最终指向done状态，start->done之间的字符即为token

   while (code[lookup] !== EOF) { //如果还有字符

       while (state !== S.done) { //开始拆分token

           //获取下一个字符
           let c = code[lookup++];
           //根据当前状态和下一个字符判断DFA如何跳转
           switch (state) {
               case S.start: //开始为空集,实现DFA中各个状态转移分支
                   if (isDigit(c)) {
                       state = S.num;
                   } else if (isValidId(c)) {
                       state = S.id;
                   } else if (isBlank(c)) {
                       state = S.done;
                   } else if (c === '=') {
                       currentToken = [TT.assign, '=']
                       state = S.done;
                   } else if (c === '+') {
                       currentToken = [TT.plus, '+']
                       state = S.done;
                   } else if (c === ';') {
                       currentToken = [TT.semicolon, ';']
                       state = S.done;
                   };
               break;
               case S.num: //如果是整数
                   if (isDigit(c)) {
                       state = S.num;
                   } else {
                       currentToken = [TT.num, code.slice(index,lookup - 1)];
                       lookup -= 1; //从数字状态跳出后，最后一位需要参与下一轮分词，故回退一位
                       state = S.done;
                   }
               break;
               case S.id: //如果是标识符状态
                   if (isValidId(c)) {
                       state = S.id;
                   } else {
                       let tempToken = code.slice(index,lookup - 1);
                       lookup -= 1; //从标识符状态跳出后，最后一位需要参与下一轮分词，故回退一位
                       if (isKeywords(tempToken)) {
                           currentToken = [TT.keywords, tempToken];
                       }else{
                           currentToken = [TT.id, tempToken];
                       }
                       state = S.done;
                   }
               break;                
           }
       }
       //state = S.done时跳出
       currentToken && console.log(currentToken);
       currentToken = undefined;

       //起指针跟上末指针
       index = lookup;

       //开始下一轮分词
       state = S.start;
   }
}

3.4 查看分词结果

运行上述代码即可看到目标程序片段的分词结果：

四. 小结

至此，我们就得到了元组形式的分词结果，完成了编译中第一步lexical analysis的部分，笔者同时提供了一份包含token所在行列信息的版本，你可以从附件或【我的github仓库】中拿到示例代码，如果觉得对你有帮助，可以在github上为我加个星星哦~

demo.rar

md原文.rar

作者：大史不说话