李航-机器学习-感知机(perceptron)-原始形式
机器学习-感知机(perceptron)
感知机模型
- 感知机模型
- 感知机学习策略
- 感知机算法实现
- 代码实现
- 运行程序可得
- 运行程序
感知机模型
感知机是一种线性的、二类分类模型,可以将空间划分为正类和负类,是一种判别模型,输入为具体的实例,输出为实例的类别(+1,-1)。有原始形式和对偶形式两种。感知机是神经网络和支持向量机的基础。
感知机预测是利用学习到的模型对输入实例进行类别的划分。
由输入空间到输出空间有如下函数:
f(x) = sign(w*x+b)
感知机学习策略
假设数据集是线性可分(可以使用一个超平面完全将正负数据划分开来),我们要做的就是找到一个线性函数将训练集中的正负实例点完全划分开来。
线性函数中的未知参数是w、b,所以我们的任务就是找到满足上述条件的参数值,若要找到相应的参数值,就需要通过损失函数来寻找w、b。
我们可以选用误分类点的总数作为我们的损失函数,但是这样的损失函数中的参数w、b不是连续变化的,在后面不利于求导优化。所以我们选择的损失函数是误分类点到初始超平面的距离总和。公式如下:

||w||为w的L2范数:w的平方开根号
所有误分类点到超平面的距离为:

在李航的书中不考虑1/||w||,由此得到损失函数,我还没弄清怎么回事。
综上,感知机sign(w*x+b)的损失函数为:
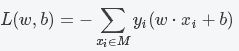
M是误分类点的总数,这个函数就是感知机的经验风险函数。
感知机算法实现
输入:训练数据集T={(x1,y1),(x2,y2),(x3,y3)…},xi属于实数集,yi={1,-1},学习率n
输出:w,b;感知机函数f(x) = sign(wx+b)
(1)、选取初值w0,b0
(2)、在训练集中选取数据(xi,yi)
(3)、将训练集中选取的数据带入yi(wxi+b),如果该式小于零,那么就对w,b进行更新:w<-w+nxiyi,b<-b+nb
(4)、转回(2),直到训练集中所有的点都能使yi(wxi+b)大于零
代码实现
import numpy as np //用于各种数值运算,例如矩阵,矩阵内积等
import random as random //用于打乱数据顺序
import matplotlib as mpl
import matplotlib.pyplib as plt
//定义数据集
datas =[[(1,2),-1],[(2,1),-1],[(2,2),-1],[(1,4),1],[(3,3),1],
[(5,4),1],[(3, 3), 1], [(4, 3), 1], [(1, 1), -1],[(2, 3), -1], [(4, 2), 1]]
//将数据集打乱
random.shuffle(datas)
//输入图像标题
fig = plt.figure('Input data')
//从datas中依次取出元素
xArr = np.array([x[0] for x in datas]) //取出一个11*2的数组
yArr = np.array([x[1] for x in datas])//取出每一个标签的分类值
//分别初始化数据集中正类和负类的空数组
xPlotx,xPloty,xPlotx_,xPloty_ = [],[],[],[]
// 利用循环分别存储正类和负类数据
for i in range(len(datas)):
y = yArr[i] //读取标签值
if y>0:
xPlotx.append(xArr[i][0])//x为数组中第一列的值
xPloty.append(xArr[i][1])//y为数组中第二列的值
else:
xPlotx_.append(xArr[i][0])
xPloty_.append(xArr[i][2])
//图像标题
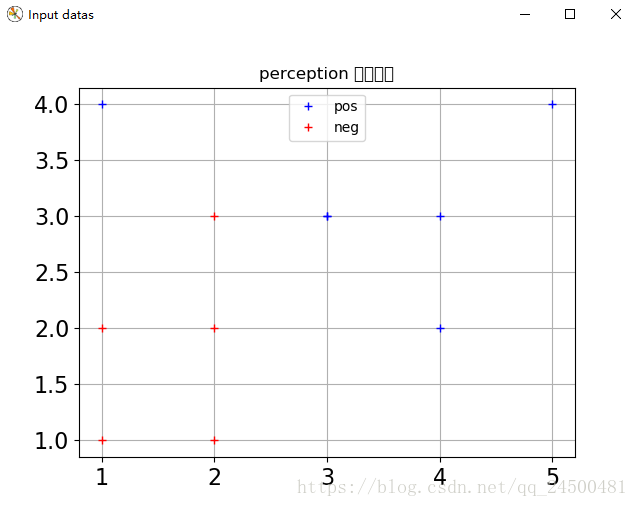
plt.title('percetron 输入数据‘)
//图像显示网格线
plt.grid(True)
//绘制数据集中的正负类点
pPlot1,pPlot2 = plt.plot(xPlotx,xPloty,'b+',xPlotx_,xPloty_,'r+')
//给图像贴标签,指定标签位置
plt.legend(handles=[pPlot1,pPlot2],labels=['pos','neg'],loc='upper center')
plt.show()
运行程序可得
//对w、b进行初始化
//给w赋初值[1,1]
w = np.array([1,1])
b = 3
//学习率
n = 1
//依次检验训练集中的数据
while True:
num = 0
for i in range(len(datas)):
num+=1 //每取出一个数据,记录加一
x = xArr[i]
y = yArr[i]
z = y*(np.dot[w,x]+b) //带入公式y(w*x+b),np.dot用于计算矩阵的内积
if z<=0:
//对w、b进行更新
w = w + n*x*y
b = b+n*b
break
//当取出的数据个数大于或者等于数组长度
if num>=len(datas):
break
fig = plt.figure('Output figure')
x0 = np.linespce(0,5,100)//生成从0到5的100个等间隔数
w0 =w[0]
w1 = w[1]
x1 = -(w0/w1)*x0-b/w1
plt.title("Perception 输出平面")
plt.xlabel('x0')
plt.ylabel('x1')
plt.annotate('Output Hyperplane',xy=(0.5,4.5),xytext=(1.7,3.5))//第一个参数为注释文本内容,xy为被注释的坐标点,xytext为注释文字坐标位置
plt.plot(x0,x1,'k', lw=1)
pPlot3, pPlot4= plt.plot(xPlotx,xPloty,'b+',xPlotx_,xPloty_,'rx')//绘点
plt.legend(handles = [pPlot3,pPlot4],labels=['Positive Sample','Negative Sample'],loc='upper right')
plt.show()