【秋招】携程_数据分析岗_面试题整理
1. spark用过吗?那你觉得和MR这两个计算框架中间产生的数据倾斜怎么处理
1)数据倾斜指的是key的分布严重不均,如wordCount中,有80%的数据都是('aaa',1),这样大部分数据交给一个reduce,剩下的20%数据分散到不同的reduce处理
2)造成数据倾斜的原因:
a. group by维度小,某值数量多
b. distinct 遇见某较多的特殊值
c. join 某个表比较小,导致key集中
d. join 两个大表,但是分桶的判断字段0值或空值过多,这些0值和控制都由一个reduce处理
3)mapreduce处理数据倾斜:
a. 调优参数
i:set hive.map.aggr=true:在map中做部分聚集操作,效率更高但需要更多内存
ii:set hive.groupby.skewindata=true:生成查询会有两个MRjob,第一个job中map的输出结果会随机分布到reduce中,相同group by key可能分到不同reduce中;第二个job再根据预处理的结果按照groupby key分布到reduce中
b. 将倾斜的key分成多组,如'aaa'分成'aaa1'、'aaa2'等
c. 能先进行 group 操作的时候先进行 group 操作,把 key 先进行一次 reduce,之后再进行 count 或者 distinct count 操作
d. join 操作中,使用 map join 在 map 端就先进行 join ,免得到reduce 时卡住
e. 加个combiner函数,加上combiner相当于提前进行reduce,就会把一个mapper中的相同key进行了聚合,减少shuffle过程中数据量,以及reduce端的计算量
f. 大小表join:使用map join让小的维度表(1000条以下的记录条数) 先进内存。在map端完成reduce
g. 大表join大表:把空值的key变成一个字符串加上随机数,把倾斜的数据分到不同的reduce上,由于null值关联不上,处理后并不影响最终结果
h. 空值情况:count distinct时,将值为空的情况单独处理,如果是计算count distinct,可以不用处理,直接过滤,在最后结果中加1。如果还有其他计算,需要进行group by,可以先将值为空的记录单独处理,再和其他计算结果进行union
i. groupby 维度过小:采用sum() group by的方式来替换count(distinct)完成计算
(参考:https://www.zhihu.com/question/27593027,https://www.cnblogs.com/kinginme/p/7070638.html)
2. 我们工作需要用到一点AI算法,你挑一个讲讲吧
略。
3. 问了dbscan
1)属于密度聚类方法
2)基于邻域来描述样本集的紧密程度,由密度可达关系导出最大密度相连的集合
3)过程:
a. 定义距离和最小子样本集大小minPts
b. 根据距离和minPts找到核心对象
c. 随机选择一个核心对象,找到核心可达的核心对象集合,形成聚类
d. 重复c过程,直到遍历所有核心对象
4)优点:
a. 可用于任意形状的稠密数据
b. 对异常点不敏感(不属于任何核心对象的,一般认为噪声点)
c. 对初始值不敏感(除了一个点同时属于两个核心对象的情况,这种情况下会采用先来后到进行点的归类)
5)缺点:
a. 密度不均匀、聚类间距差距大,效果差
b. 相对于kmeans调k,dbscan需要调disntance和minPts,调参难度会大一些
c. 样本集大时,收敛慢,因为要做距离计算,可以建立kd tree改进
(参考:https://www.cnblogs.com/pinard/p/6208966.html)
4. 问了核函数
一些模型中我们需要将特征映射到高维空间再进行分割(如SVM),这时候我们需要先把x转换到高维空间z,然后在高维空间对z进行内积计算,当维度特别高时,计算量特别大。那么我们能不能偷吃步,把映射到高维空间和内积计算放在一起计算,降低计算量?
如果低维空间中存在一个函数K(x,x'),它正好等于高维空间中的内积计算,即K( x, x′) =<φ( x) ⋅φ( x′) > ,那么我们称其为核函数。
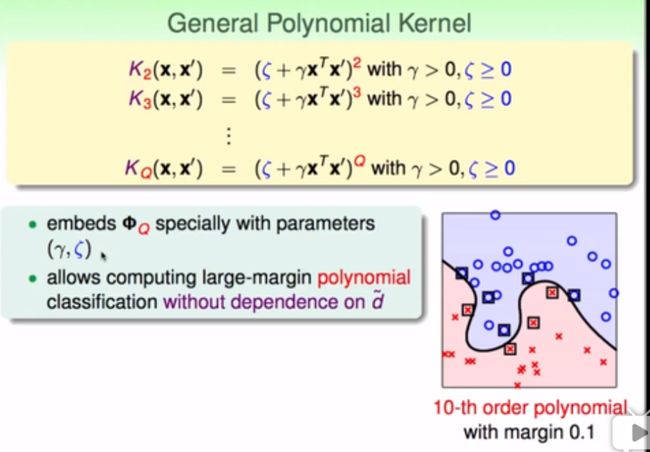
1)多项式核函数:
a. 假设一个转换函数,它会求x内两两元素的组合,从而将x映射到高维空间z。在高维空间求内积,经过化简,我们发现可以表示成低维空间X的内积计算
b. 对现有核函数进行一些微小的改动,就可以使算式更一般,也更容易 计算,并能投影到更复杂的空间中
c. 进一步,我们也可以对指数进行转换。这时候我们就能投影到更复杂的空间中去
2)线性核函数:当多项式核函数的指数为1,就退化为线性核函数
3)高斯核函数:
a. 将高斯函数进行泰勒展开,发现它包含着无限多维的转换
b. 更一般的高斯核函数
4)sigmoid核函数:
a. κ(x,xi)=tanh(η
b. 采用sigmoid核函数,支持向量机实现的就是一种多层神经网络
(参考:林轩田《机器学习技法》第3课“kernel核函数”;https://blog.csdn.net/batuwuhanpei/article/details/52354822)
5. 现场写SQL
略。
6. 随机森林
1)随机森林原理:通过构造多个决策树,做bagging以提高泛化能力
2)随机方法包括:subsample(有放回抽样)、subfeature、低维空间投影(特征做组合,参考林轩田的《机器学习基石》)
3)有放回抽样,可以用包外样本做检验
4)也可以用OOB做特征选择,思路:
a. 如果一个特征有效,那么这个特征引入杂质会明显影响模型效果
b. 引入杂质会影响分布,所以更好的方式是对特征中的取值进行洗牌,然后计算前后模型的差异
c. 但是我们不想训练两个模型,可以利用OOB进行偷懒。把OOB中的数据该特征取值洗牌,然后扔进训练好的模型中,用输出的结果进行误差检验
7. 数据清理
1)缺失值处理
a. 删(横删、竖删、成对删)
b. 均值、中位数、众数填充
c. 建模填充
d. 映射到高维空间(如onehot)
2)异常值/噪声处理
a. 删
b. 上下截取(winsorzion)
c. 转为缺失值,用缺失值处理的方法处理
d. 分箱
e. PCA等降维方法,去噪声字段
f. 聚类去噪声点
3)唯一性处理
a. 去重
b. 对于数据不一致情况,判断数据来源的权威性
4)量纲不一致
a. 标准化(最大最小、z标准化)
b. 归一化(对文本、评分类数据)
5)格式异常
8. 给一个实际场景,怎么分析数据,怎么提取数据特征
略。