机器学习系列之 感知器模型

前言

感知器模型是线性分类模型的一个基本模型，是当今主流的神经元基本结构，掌握好感知器模型有利于我们的机器学习进一步学习，这里简单介绍下感知器模型并且用Python代码演示。
如有谬误，请联系指正。转载请注明出处。
联系方式：
e-mail: [email protected]
QQ: 973926198
github: https://github.com/FesianXu
代码开源：click

---

线性分类模型与线性回归模型的区别

　　在线性回归模型中我们谈到了线性回归模型，而机器学习中很多任务是涉及到分类任务的，单纯的回归模型不能离散输出而只能连续输出，比如只能连续输出区间[0, 1]的值，而不能离散输出0或者1，因此需要对线性回归模型进行一定的改造才能变为线性分类模型。下图为线性回归模型的图示，这个也称为一个神经元：
　　
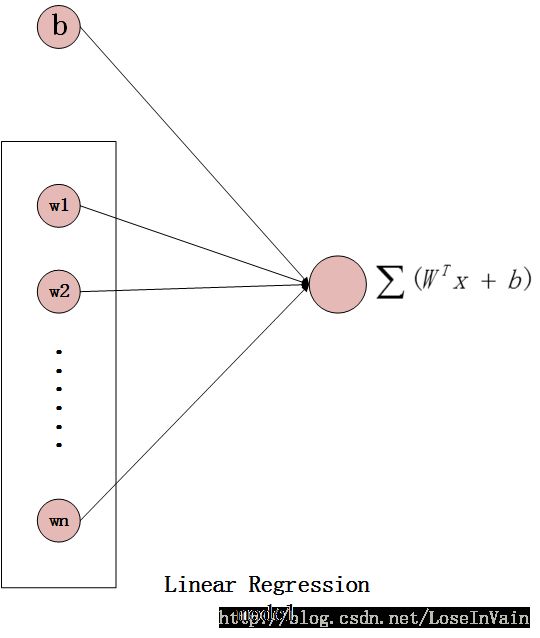
　　进行所谓的‘改造’指的是在神经元的输出端添加一个激活函数，使得输出从连续取值变为离散输出如0或者1。

感知器模型

　　在经典的感知器模型(Perceptron)中，在输出端添加了一个阶跃函数（Step Function），这样就将输出离散到了0或者1，表达式如：

ϕ(x)={10x≥0x<0

添加了激活函数之后，整个感知器模型的表达式就变为了：

ϕ(∑i=1mWTx+b)

激活函数图像如：

经过改造后的模型示意图如：

这个模型类似于线性回归模型，参数共有 WT 和 b ，因此在训练过程中需要学习到这两个参数。

训练策略

　　感知器采用的训练策略和线性回归，BP反向传播算法等是不同的，感知器采用了激活函数，而且这个激活函数 ϕ(x) 是不可导的，因此误差函数的梯度将会没有办法传播到输入层的权值中，因此不能采用梯度反向传播的策略去学习参数，我们在感知器中，采用的是误差驱动更新的策略，也就是将误分类的样本用来更新参数，将正确分类的样本忽略，当所有样本都是正确分类时，就训练完成。而在更新参数的过程中，我们采用的策略是：

w:=w+η∗yi∗xi

b:=b+η∗yi

其中 yi 是误分类的类别，分为 +1 和 −1 ，而 xi 是误分类的样本的特征， η 是学习率

再说激活函数

　　感知器里采用的激活函数用的是阶跃函数，因为阶跃函数不能求导，参数学习策略采用的是错误驱动更新。这个做法其实是不利于感知器搭建成为一个更深的网络的，因为更深更大的网络将会涉及到更多的海量参数，如果靠这种错误驱动的方法去更新参数，将会使得这个优化过程不可控制，难以收敛，更为理想的激活函数应是可以求导的，这样才能使得网络的输出误差可以通过反向传播误差和梯度传递到各层，以至于可以通过梯度去指导更新参数，这样会大大加速网络参数训练的速度。在后面的文章中，我们会看到sigmoid函数或者是Logistic函数，ReLU函数，tanh函数将会是更好的选择。

代码演示，基于Python和numpy

数据描述

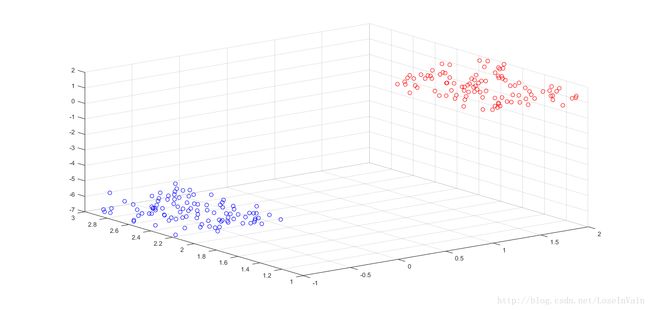
　　我们这里采用的数据仍然是人工生成的数据，维度为三维，分为两类，一类为1而另一类为0（另一类储存的时候为0的目的是因为激活函数判断生成的是0和1，因此需要设置为0才能进行判断，这里是可以将传统的阶跃函数更改为如下形式的）

ϕ(x)={1−1x≥0x<0

数据可视化之后是：

数据储存格式如：

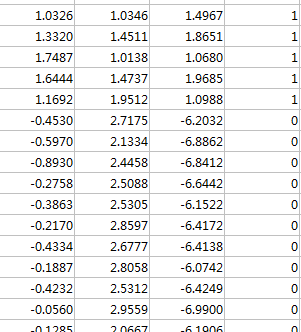
其中每一行是一个样本点，前三列是维度，最后一列是类别label。

代码

数据处理部分

import numpy as np
import scipy.io as sio
import random
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

path = u'F:\笔记\人工智能\感知器\\samples.mat'
mat = sio.loadmat(path)
dataset = mat['samples']
params = {
    'w': np.random.normal(size=(3, 1)),
    'b': np.random.normal(size=(1))
}


def predict(batch):
    logits = np.dot(batch, params['w'])+params['b']
    return 1*(logits > 0)+(-1)*(logits < 0)

def regression(x, y):
    w1 = params['w'][0]
    w2 = params['w'][1]
    w3 = params['w'][2]
    return -w1/w3*x-w2/w3*y-params['b']/w3

learning_rate = 0.001
# 采用错误驱动的方式去更新参数，因为感知器的阶跃函数不能传递梯度。
def random_get_data(dataset, batch_size):
    batch_id = random.sample(range(dataset.shape[0]), batch_size)
    ret_batch = dataset[batch_id, 0:3]
    ret_label = dataset[batch_id, 3]
    return ret_batch, ret_label

主要训练部分

batch_size = 128
for each_epoch in range(10000):
    ret_batch, ret_label = random_get_data(dataset, batch_size)
    result = predict(ret_batch)
    ret_label = np.reshape(ret_label, (batch_size, 1))
    ret_label = (ret_label == 0)*(-1.0)+(ret_label == 1)*1.0
    err = (ret_label != result)*1.0  # 为1的是分类错误的，需要驱动更新
    err_batch = np.concatenate((ret_batch, err), axis=1)
    err_id = np.where(err_batch[:, 3] == 1)
    if len(err_id[0]) != 0:
        id = err_id[0][0]
        batch = np.reshape(np.transpose(err_batch[id, 0:3]), (3, 1))
        params['w'] = params['w']+learning_rate*ret_label[id]*batch
        params['b'] = params['b']+learning_rate*ret_label[id]
    else:
        break

绘图部分

fig = plt.figure()
ax = Axes3D(fig)
x = dataset[0:100, 0]
y = dataset[0:100, 1]
z = dataset[0:100, 2]
ax.scatter(x, y, z, c='b')
x = dataset[100:200, 0]
y = dataset[100:200, 1]
z = dataset[100:200, 2]
ax.scatter(x, y, z, c='r')
X = np.arange(-5, 5, 0.25)
Y = np.arange(-5, 5, 0.25)
# 网格化数据
X, Y = np.meshgrid(X, Y)
ax.plot_surface(X, Y, regression(X, Y), cmap='rainbow')
print(params['w'][0])
print(params['w'][1])
print(params['w'][2])
print(params['b'][0])
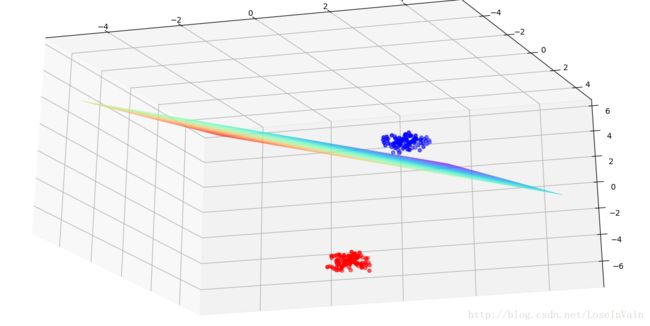
plt.show()

训练结果

结果分析

从训练结果图中，我们可以看到，虽然感知器训练出来的线性超平面可以将两类数据完美地分割开，但是其边界距离其中某个类很近，离某个类很远，如果蓝色类出现一个采样噪声，那么很可能超平面就把它给分类错了，这样的超平面的泛化性能是很差的，因此我们需要更具有鲁棒性的算法，SVM是一个更好的选择，我们以后将会开始介绍SVM。