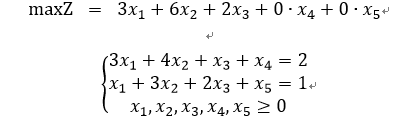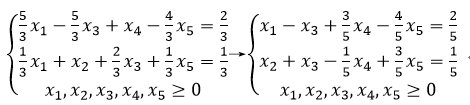单纯形表格法求最值详解-组合数学
解:
(1) 对原式引进松弛变量 x 4 , x 5 x_4,x_5 x4,x5,可得:
(2) 建立初始单纯形表格
A i Ai Ai:表示基变量,初始挑选单位阵为初始基,构成向量B
C B C_B CB:代表基变量在目标函数中的系数向量
C C C:代表目标函数的系数。在此题中, C = ( 3 , 6 , 2 , 0 , 0 ) C=(3,6,2,0,0) C=(3,6,2,0,0)
P i Pi Pi:表示引进松弛变量后限制方程组的列系数, P 0 P0 P0代表等式右侧常量。
z z z:代表当前最优解
σ i σ_i σi:代表非基变量的检验数
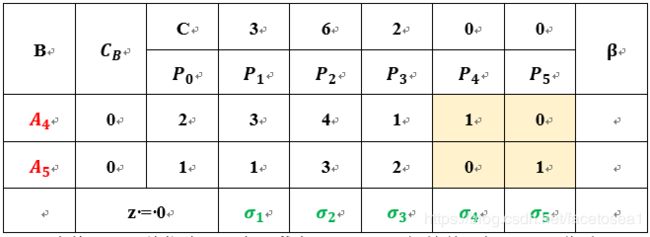
由表格可知,单位阵出现在淡黄色阴影区,故初始基选择 x 4 , x 5 x_4,x_5 x4,x5。此时更新B列。
(3) 第一轮更新表格
① 进基:由非基变量→基变量的决策变量,我们称之为进基变量,挑选原则:

那么 x k x_k xk进基。

可知: m a x 〖 σ j ∣ σ j > 0 〗 = σ 2 = 6 , k = 2 , 因 此 x 2 max〖{σ_j |σ_j>0}〗=σ_2=6,k=2,因此x_2 max〖σj∣σj>0〗=σ2=6,k=2,因此x2进基。
② 退基:由基变量→非基变量,称之为退基,退基原则:
![]()

由上可知 β 1 ( = β ( A 4 ) ) > β 2 ( = β ( A 5 ) ) β_1 (=β_(A_4 ))>β_2 (=β_(A_5 )) β1(=β(A4))>β2(=β(A5)),因此 x 5 退 基 , x 2 代 替 x 5 进 基 , x 4 保 留 仍 为 基 变 量 , 主 元 素 为 a 2 2 = 3 x_5退基,x_2代替x_5进基,x_4保留仍为基变量,主元素为a_22=3 x5退基,x2代替x5进基,x4保留仍为基变量,主元素为a22=3,在单纯形表中用()表示。

③ 由①、②,我们完成第一次基变量更新,执行完①、②当前基变量为 x 2 、 x 4 x_2、x_4 x2、x4。选定基变量,清空表格。
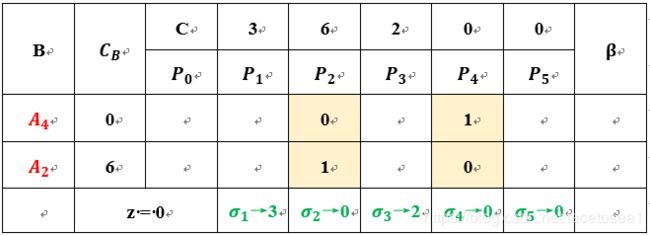
由于基变量改变,因此需要根据新的基变量,对约束恒等方程式进行等价变换。

再次更新表格可得:
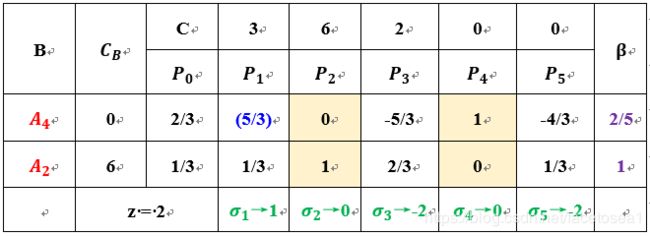
(4) 第二轮更新表格
① 进基:由非基变量→基变量的决策变量,我们称之为进基变量,挑选原则:

那么 x k x_k xk进基。
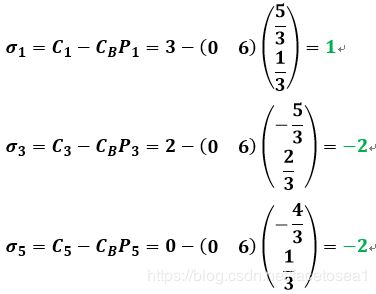
可知: m a x 〖 σ j ∣ σ j > 0 〗 = σ 1 = 1 , k = 1 , max〖{σ_j |σ_j>0}〗=σ_1=1,k=1, max〖σj∣σj>0〗=σ1=1,k=1,因此 x 1 x_1 x1进基。
② 退基:由基变量→非基变量,称之为退基,退基原则:
![]()
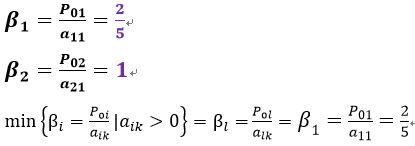
由上可知 β 1 ( = β ( A 4 ) ) < β 2 ( = β ( A 2 ) ) β_1 (=β_(A_4 ))<β_2 (=β_(A_2 )) β1(=β(A4))<β2(=β(A2)),因此 x 4 x_4 x4退基, x 1 x_1 x1代替 x 4 x_4 x4进基, x 2 x_2 x2保留仍为基变量,主元素为 a 1 1 = 5 / 3 a_11=5/3 a11=5/3,在单纯形表中用()表示。
③ 由①、②,我们完成第二次基变量更新,执行完①、②当前基变量为 x 2 、 x 1 x_2、x_1 x2、x1。选定基变量,清空表格。
由于基变量改变,因此需要根据新的基变量,对约束恒等方程式进行等价变换。
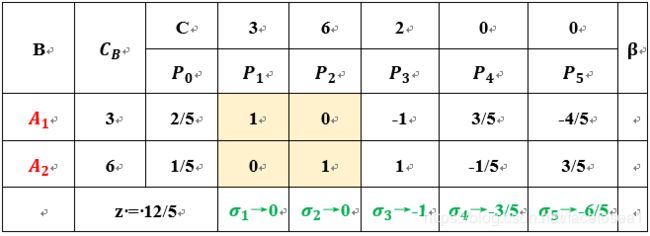
(5) 第三轮更新表格
① 进基:

由于 σ 3 、 σ 4 、 σ 5 σ_3、σ_4、σ_5 σ3、σ4、σ5均小于0,因此当前z取得最优解。最优解为: x 1 = 2 / 5 x_1=2/5 x1=2/5, x 2 = 1 / 5 x_2=1/5 x2=1/5,目标函数 z = 12 / 5 z=12/5 z=12/5
最终表格: