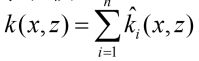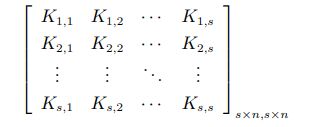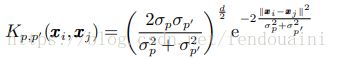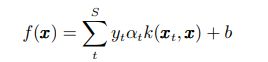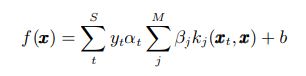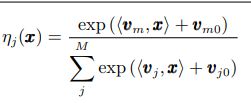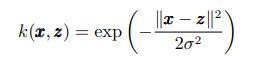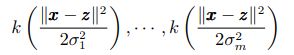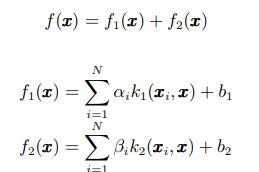多核学习方法介绍

作者 | Walker

本文为SVM多核学习方法简介的续篇。

通过上篇文章的学习，我们知道，相比于单个核函数，多核模型可以具有更高的灵活性。经过多个核函数映射后的高维空间是由多个特征空间组合而成的组合空间，而显然组合空间可以组合各个子空间不同的特征映射能力，能够将异构数据中的不同特征分量分别通过最合适的单个核函数进行映射，最终使得数据在新的组合空间中能够得到更加准确、合理的表达，进而提高样本数据的分类正确率或预测精度。

 

多核学习方法根据不同的分类标准有不同的分类方式，按照多核函数的构造方法和特点的不同，可以将多核学习方法大致分成三大类别：合成核方法、多尺度核方法、无限核方法。

 

一、合成核方法

把具有不同特性的多个核函数进行组合，就会得到包含各个单核函数的总体特性的多核函数。多核函数形成的方式本身就使得多核函数具有更加准确、更加强大的映射能力或者分类能力，特别是对于实际应用中样本数据具有比较复杂分布结构的分类、回归等学习问题，多核学习的优点非常明显。

 

（1）多核线性组合合成方法

多核线性组合方法是将基本核函数进行线性组合，用表达式可以如下所示描述：

假设变量 x,z ∈X，其中 X 属于 R（n）空间，非线性函数Φ能够实现输入空间 X到特征空间 F 的映射，其中 F ∈R（m），m>>n。假设已知的基本核函数为k (x,z) ，再将其进行归一化为ˆk(x,z)，则可以通过以下方式进行线性组合得到多核函数：

直接求和核其中， 其中 ˆk(x,z) 为第 i 个基本核函数。

 

加权求和核，其中βi为第 i 个核函数的权值。

多项式加权扩展核，其中kp(x,z)是k (x,z) 的多项式扩展。

 

（2）多核扩展合成方法

上述描述的多核组合方法主要是基于将基本核函数直接求和或者加权求和的思想实现多个核函数的结合，但这样的方法最大的问题是可能丢失原始数据的某些特征信息，比如数据分布的某块区域包含很多信息并且是多变的，当使用平均或者加权平均的方式将该部分数据“平滑”之后，能够表示多变信息的数据很有可能被不用的核函数给平滑掉，有可能导致最终的特征信息不完整，降低分类器的分类能力和准确性，基于上述考虑，产生了将原有多核矩阵进行扩展合成的方法，也就是最终能够使用的多核矩阵是由原先的单个核矩阵和其核矩阵共同构成的。因此, 原始核函数的性质得以保留。该合成核矩阵的形式为：

 

可以看出, 原始核矩阵位于新矩阵的对角线上. 其他所有元素是定义为 (Kp,p0 )i,j = Kp,p0 (xi , xj ) 的两个不同核矩阵的混合, 可由如下公式求得 (以两个 高斯核为例):

 

很明显,当p = p 0 时, Kp,p ≡ Kp.实验结果显示,当数据集具有变化的局部数据分布时,这种合成核方法将是更好的选择.此外, 通常核组合方法在很大程度上依靠训练数据,并且必须通过学习获取一些权系数,以标识每个核的重要性.

 

（3）非平稳多核学习

前边的多核线性组合方法都是对核函数的平稳组合, 即对所有输入样本, 不同的核对应的权值是不变的, 无形中对样本进行了一种平均处理.Lewis 提出了一种多核的非平稳组合方法, 对每个输入样本配以不同的权值系数.如常规 SVM判别函数为：

引入不同的加权系数, 典型的合成核 SVM 的判别函数可以改写为：

在最大熵判别框架下, 通过使用一种大间隔隐变量生成模型, 使得隐参数估计问题可以通过变化边界和一个内点优化过程来表示, 并且相应的参数估计可以通过快速的序列最小优化算法实现。

 

（4）局部多核学习

针对多核学习在整个输入空间中对某个核都是分配相同权值的问题, 利用一种选通模型 (Gating model) 局部地选择合适核函数, 提出了一种局部多核学习算法. 在SVM 框架下, 其判别函数形如:

这里的vm 和vm0 是选通模型参数, 可以在多核学习过程中通过梯度下降法获得.将局部选通模型和基于核的分类器相结合,优化问题可以用一种联合的方式加以解决。

 

二、多个尺度的多核学习: 多尺度核方法

合成核方法虽然有了一些成功应用,但都是根据简单核函数的线性组合, 生成满足Merce条件的新核函数;核函数参数的选择与组合没有依据可循,对样本的不平坦分布仍无法圆满解决,限制了决策函数的表示能力。在此情况下,出现了多核学习的一种特殊化情形,即将多个尺度的核进行融合。这种方法更具灵活性, 并且能比合成核方法提供更完备的尺度选择.此外,随着小波理论、多尺度分析理论的不断成熟与完善,多尺度核方法通过引入尺度空间,使其具有了很好的理论背景。

 

多尺度核方法的基础就是要找到一组具有多尺度表示能力的核函数. 在被广泛使用的核函数中, 高斯径向基核是最受欢迎的, 因为它们具有通用普遍的近似能力,同时它也是一种典型的可多尺度化核. 以此核为例,将其多尺度化 (假设其具有平移不变性):

其中, σ1 < · · · < σm. 可以看出, 当σ较小时, SVC可以对那些剧烈变化的样本进行分类; 而当σ较大 时, 可以用来对那些平缓变化的样本进行分类, 能得到更优的泛化能力. 具体实现时,σ的取值可以借鉴 小波变换中尺度变化的规律, σ可由下式定义:

对多尺度核的学习方法：
很直观的思路就是进行多尺度核的序列学习. 多尺度核序列合成方法。简单理解就是先用大尺度核拟合对应决策函数平滑区域的样本, 然后用小尺度核拟合决策函数变化相对剧烈区域的样本, 后面的步骤利用前面步骤的结果,进行逐级优化,最终得到更优的分类结果。考虑一个两尺度核 k1 和 k2 合成的分类问题. 我们要得到合成的决策函数:

设想k1是一个大尺度的核函数(如σ较大的径 向基函数),相关的核项系数 αi 选择那些决策函数f(x)光滑区域对应的支持向量而k2是小尺度核函数,核项系数βi选择那些决策函数f(x)剧烈变化区域对应的支持向量.具体方法是: 首先通过大尺度的单核 k1 构造函数f1(x),这样,该函数可以很好地拟合光滑区域,但在其他地方存在显著误差,可以使用相对较小的松弛因子来求取αi;然后,在 f1(x)基础上使用小尺度的核 k2 构造 f2(x), 使得联合函数 f1(x) + f2(x)比f1(x) 具有更好的拟合性能.这种方法实际上是多次使用二次规划以实现参数的获取,运算复杂度较高, 同时支持向量的数量大量增加。

 

三、从有限向无限核的扩展 : 无限核方法

合成核与多尺度核方法都是在有限个核函数线性组合前提下加以讨论的。但对一些大规模问题,基于有限个核的多核处理方法不一定有效,多核融合的决策函数的表示能力也不能达到处处最优。 此外,在一个多尺度核函数族中, 有限个核函数的选 择并不唯一,并且其不能完备地表征这个核函数族.因此,将有限核向无限核的扩展也是一个重要的方向。

 

无限核是从由多个基本核函数的合法集合所构成的一个凸壳中找到某个核,使其能最小化凸正则化函数.与其他方法相比,这个方法有一个独有的特征, 即上述基本核的个数可以是无限多个, 仅仅需要这些核是连续参数化的.此外，用半无限规划解决来自通用核类型的核函数学习问题。

 

IKL 可以比SVM/MKL 大大提高分类正确率, 在这些情况下,IKL 能保持它的实用性, 而交叉验证和 MKL 都是不实用的。