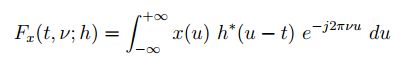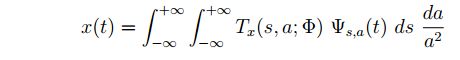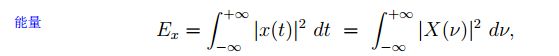时频分析方法总结：傅里叶级数及傅里叶变换、STFT 、小波变换、Wigner-Ville 分布

前言：

一、傅里叶变换的机理

一个能量无限的正弦信号和源信号乘积并求和得到某个频率下的系数，随着频率的增加，正弦信号改变，再次求得系数，依次构成了频谱图

傅里叶级数及傅里叶变换 https://blog.csdn.net/reborn_lee/article/details/80721300

傅里叶级数及傅里叶变换 https://wenku.baidu.com/view/b167af4acf84b9d528ea7a85.html（关于信号调制）

频率随时间变化-非平稳信号

平稳信号：瞬时幅度和瞬时频率是常数，相关函数仅仅取决于信号的时间差

获得非平稳信号的方式：

（1）幅度调制（2）频率调制（3）现实世界的信号

如何添加matlab工具箱：https://blog.csdn.net/BTUJACK/article/details/82183960

 

时频分析分为：常规傅立叶变换方法不能刻画任一时刻的频率成分,无法对其进行全面的分析。时频分析方法将一维时域信号变换到二维的时频平面。由于不同时频分析方法有其特有时频特性,分为：线性时频表示和非线性时频表示

线性时频分析：短时傅立叶变换、连续小波变换等,

典型的非线性时频表示有Wigner - Ville 分布、Cohen类分布、affine类分布等

二、短时傅里叶变换 STFT（gabor提出）

其中窗函数h(t)，若窗口是有限能量的则逆变换为：

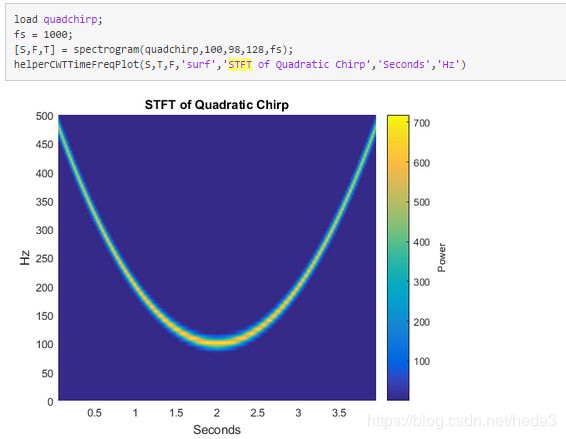
举例：对于语音信号：发音gabor，通过短时傅里叶变换（加窗口hamming 85点）可得频谱、和时频图

通过时频图可以较好的区分出每个音。 

使用：

描述：

[S,F,T] = spectrogram(quadchirp,100,98,128,fs);

函数的各参数描述： https://www.cnblogs.com/gisalameda/p/8760688.html

谱密度，功率谱，能量谱密度 https://blog.csdn.net/maxiaoyun2012/article/details/21319963

STFT的不足：窗口固定，对于时间分辨率和频率分辨率不能同时满足。h(t)窗口越短则频率分辨率越差，时间分辨率越好。

三、小波变换

连续小波变换：

 

 逆变换：

对比香农、傅里叶、STFT、小波的窗口

 

四、信号的时频分布+能量因素，也称二次变换

第一类：

（1）对短时傅里叶变换求得的能量分布

 对短时傅里叶变换的模值取平方可得能量谱但是存在的问题是有干扰项：

假如信号的成分x1(t)和x2(t)有足够的距离那么谱的重叠不那么明显。但是我们现实中分析的两个信号成分位置是不确定的。

（2）对小波变换求的能量分布

 问题：时频分辨率取决于所考虑的频率范围。

第二类：

之前的两个考虑的要么是时域的能量要么是频率的能量。现在考虑的是联合时频能量密度：

 

（3）Wigner-Ville 分布

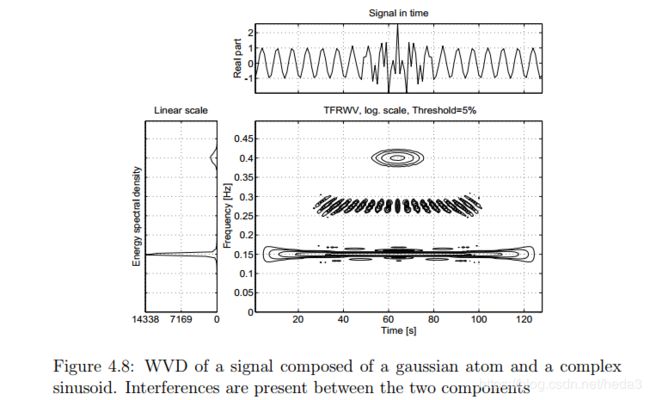
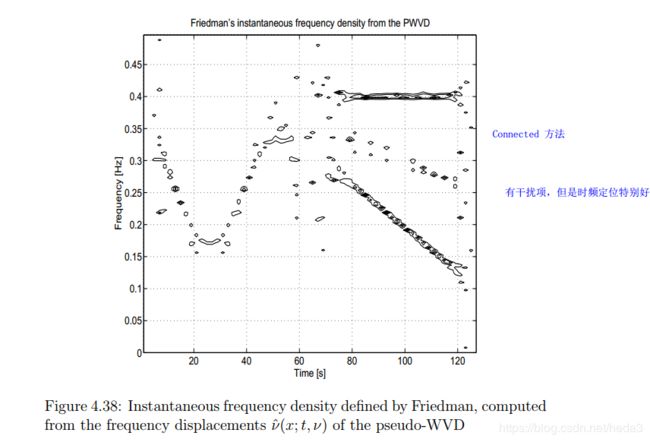
      Wigner一Ville分布定义为信号中心协方差函数的傅立叶变换，它具有许多优良的性能，如对称性、时移性、组合性、复共扼关系等，不会损失信号的幅值与相位信息，对瞬时频率和群延时有清晰的概念。
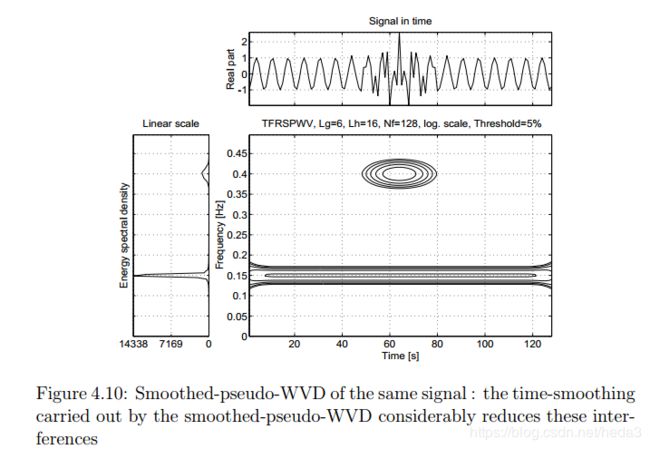
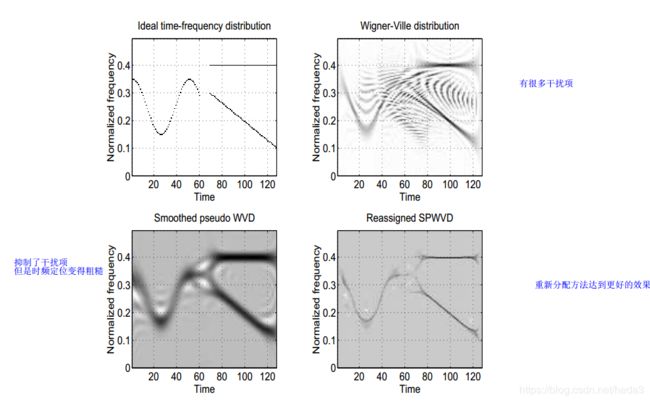
其不足是不能保证非负性，尤其是对多分量信号或具有复杂调制规律的信号会产生严重的交叉项干扰，这是二次型时频分布的固有结果，大量的交叉项会淹没或严重干扰信号的自项，模糊信号的原始特征。后续的有人对Cohen类中的核函数进行改造，提出了伪winger—ville分布、平滑伪Winger—Ville分布等各种各样的新型时频分布，对交叉项干扰的抑制起了较大的作用，但是不含有交叉项干扰且具有Winger—Ville分布聚集性的时频分布是不存在的。

（4）伪WVD（引入窗函数）

解决的问题是：对干扰项有一定的消除

 （5）平滑伪WVD分布（引入参数化函数）

3种WVD的对比：

 

 

 

 （6）模糊函数

（7）ASPWD

优势：

 （8）重新分配

不再是双线性，但此方法的成分更加集中，且有更少的干扰项。

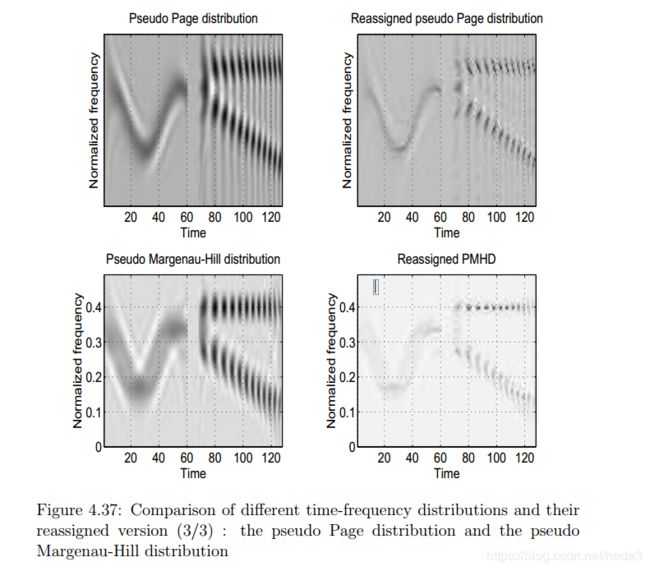
 上述几种能量分布信号的对比：

其它方法：

 

 

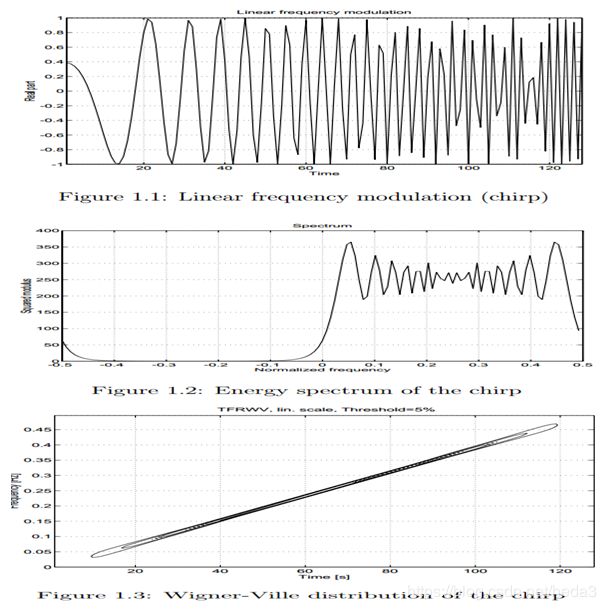
WVD的一个应用实例： 

% chip 信号的功率谱
% figure(1)
% sig1=fmlin(128,0,0.5);
% subplot(5,1,1)
% plot(real(sig1));
% title('figure1.1')

% dsp1=fftshift(abs(fft(sig1)).^2);
% subplot(5,1,2)
% plot((-64:63)/128,dsp1);
% title('figure1.2')
% subplot(5,1,3)
% tfrwv(sig1);% 时频分布
% title('figure1.3')
% %% 加入白噪声 
% subplot(5,1,4)
% sig2=sigmerge(sig1,noisecg(128),0);
% plot(real(sig2));
% title('figure1.4')
% 
% dsp2=fftshift(abs(fft(sig2)).^2);
% subplot(5,1,5)
%  plot((-64:63)/128,dsp2);
%  title('figure1.4')
% tfrwv(sig2)%时频分布

 

 

 

参考：

【1】matlab帮助

【2】时频联合分析 https://blog.csdn.net/wordwarwordwar/article/details/66583536

【3】时频分析（英文）

【4】 matlab 时频分析工具箱  https://blog.csdn.net/chenyusiyuan/article/details/2211144

   好书：

【5】感受小波 https://blog.csdn.net/chenyusiyuan/article/details/1864195