李航 《统计学习方法》第七章支持向量机习题答案
1.比较感知机的对偶形式和线性可分支持向量机的对偶性形式。
感知机原始形式: min w , b L ( w , b ) = − ∑ x i ϵ M ( y i ( w ⋅ x i + b ) ) \min_{w,b} L(w,b) = - \sum_{x_i\epsilon M}(y_i(w\cdot x_i+b)) w,bminL(w,b)=−xiϵM∑(yi(w⋅xi+b)) M M M为误分点的集合。等价于 min w , b L ( w , b ) = ∑ i = 1 N ( − y i ( w ⋅ x i + b ) ) + \min_{w,b} L(w,b) = \sum_{i=1}^N(-y_i(w\cdot x_i+b))_+ w,bminL(w,b)=i=1∑N(−yi(w⋅xi+b))+
对偶形式: w w w, b b b表示为 x i x_i xi, y i y_i yi的线性组合的形式,求其系数(线性组合的系数) w = ∑ i = 1 N α i y i x i w = \sum_{i=1}^{N}\alpha_iy_ix_i w=∑i=1Nαiyixi, b = ∑ i = 1 N α i y i b = \sum_{i=1}^{N}\alpha_iy_i b=∑i=1Nαiyi min w , b L ( w , b ) = min α i L ( α i ) = ∑ i = 1 N ( − y i ( ∑ j = 1 N α j y j x j ⋅ x i + ∑ j = 1 N α j y j ) ) + \min_{w,b} L(w,b) = \min_{\alpha_i}L(\alpha_i) = \sum_{i=1}^N(-y_i(\sum_{j=1}^{N}\alpha_jy_jx_j\cdot x_i+ \sum_{j=1}^{N}\alpha_jy_j))_+ w,bminL(w,b)=αiminL(αi)=i=1∑N(−yi(j=1∑Nαjyjxj⋅xi+j=1∑Nαjyj))+
线性可分支持向量机原始问题: min w , b 1 2 ∥ w ∥ 2 s . t . y i ( w ⋅ x i + b ) − 1 ≥ 0 \min_{w,b} \frac{1}{2}\|w\|^2\\s.t.\quad\quad y_i(w\cdot x_i+b)-1\ge0 w,bmin21∥w∥2s.t.yi(w⋅xi+b)−1≥0
线性可分支持向量机对偶问题: min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i s . t . ∑ i = 1 N α i y i = 0 0 ≤ α i ≤ C , i = 1 , 2 , ⋯ , N \min_{\alpha}\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum_{i=1}^N\alpha_i\\s.t. \quad\quad \sum_{i=1}^N\alpha_iy_i = 0\\0\leq\alpha_i\leq C,\quad i=1,2,\cdots,N αmin21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαis.t.i=1∑Nαiyi=00≤αi≤C,i=1,2,⋯,N最终 w ∗ , b ∗ w^*,b^* w∗,b∗可以按照下士求出, w ∗ = ∑ i = 1 N α i ∗ j i x i w^*=\sum_{i=1}^N\alpha_i^*j_ix_i w∗=∑i=1Nαi∗jixi, b ∗ = y j − ∑ i = 1 N α i ∗ ( x i ⋅ x j ) b^*=y_j-\sum_{i=1}^N\alpha_i^*(x_i\cdot x_j) b∗=yj−∑i=1Nαi∗(xi⋅xj)。可以看出 w , b w,b w,b实质也是将其表示为 x i , x j x_i,x_j xi,xj的线性组合形式。
2.已知正例点 x 1 = ( 1 , 2 ) T x_1=(1,2)^T x1=(1,2)T, x 2 = ( 2 , 3 ) T x_2=(2,3)^T x2=(2,3)T, x 3 = ( 3 , 3 ) T x_3=(3,3)^T x3=(3,3)T,负例点 x 4 = ( 2 , 1 ) T x_4=(2,1)^T x4=(2,1)T, x 5 = ( 3 , 2 ) T x_5=(3,2)^T x5=(3,2)T,试求最大间隔分离超平面和分类决策函数,并在图上画出分离超平面,间隔边界以及支持向量。
手动计算:根据题意,得到目标函数即约束条件 min 1 2 ∥ w 1 2 + w 2 2 ∥ s . t . w 1 + 2 w 2 + b ≥ 1 ( 1 ) 2 w 1 + 3 w 2 + b ≥ 1 ( 2 ) 3 w 1 + 3 w 2 + b ≥ 1 ( 3 ) − 2 w 1 − w 2 − b ≥ 1 ( 4 ) − 3 w 1 − 2 w 2 − b ≥ 1 ( 5 ) \min\frac{1}{2}\|w_1^2+w_2^2\|\\s.t.\quad w_1+2w_2+b\ge 1\quad\quad(1)\\ \quad\quad\quad 2w_1+3w_2+b\ge 1\quad\quad(2)\\ \quad\quad\quad 3w_1+3w_2+b\ge 1\quad\quad(3)\\ \quad\quad\quad -2w_1-w_2-b\ge 1\quad\quad(4)\\ \quad\quad\quad -3w_1-2w_2-b\ge 1\quad\quad(5) min21∥w12+w22∥s.t.w1+2w2+b≥1(1)2w1+3w2+b≥1(2)3w1+3w2+b≥1(3)−2w1−w2−b≥1(4)−3w1−2w2−b≥1(5)
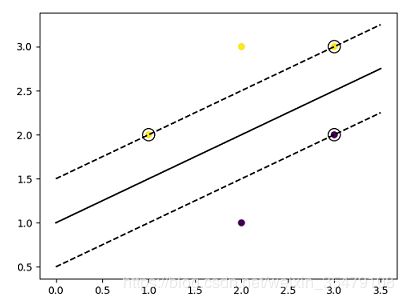
以 w 1 . w 2 w_1.w_2 w1.w2为坐标轴找到可行域,目标函数即求到原点距离最小的点,也就是 w = [ − 1 , 2 ] w=[-1,2] w=[−1,2],对于正例点 b ≥ − 2 b\ge-2 b≥−2,对于负例点 b ≤ − 2 b\le -2 b≤−2,所以 b = − 2 b=-2 b=−2。
python实验验证:
from sklearn import svm
x=[[1, 2], [2, 3], [3, 3], [2, 1], [3, 2]]
y=[1, 1, 1, -1, -1]
clf = svm.SVC(kernel='linear',C=10000)
clf.fit(x, y)
print(clf.coef_)
print(clf.intercept_)
画图
import matplotlib.pyplot as plt
import numpy as np
plt.scatter([i[0] for i in x], [i[1] for i in x], c=y)
xaxis = np.linspace(0, 3.5)
w = clf.coef_[0]
a = -w[0] / w[1]
y_sep = a * xaxis - (clf.intercept_[0]) / w[1]
b = clf.support_vectors_[0]
yy_down = a * xaxis + (b[1] - a * b[0])
b = clf.support_vectors_[-1]
yy_up = a * xaxis + (b[1] - a * b[0])
plt.plot(xaxis, y_sep, 'k-')
plt.plot(xaxis, yy_down, 'k--')
plt.plot(xaxis, yy_up, 'k--')
plt.scatter (clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=150, facecolors='none', edgecolors='k')
plt.show()
3.线性支持向量机还可以定义为以下形式: min w , b , ξ 1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i 2 s . t . y i ( w ⋅ x i + b ) ≥ 1 − ξ i , i = 1 , 2 , ⋯ , N ξ i ≥ 0 , i = 1 , 2 , ⋯ , N \min_{w,b,\xi}\quad \frac{1}{2} \|w\|^2+C\sum_{i=1}^N\xi_i^2\\s.t.\quad y_i(w\cdot x_i+b)\ge 1-\xi_i,\quad i=1,2,\cdots,N\\\xi_i\ge 0,\quad i=1,2,\cdots,N w,b,ξmin21∥w∥2+Ci=1∑Nξi2s.t.yi(w⋅xi+b)≥1−ξi,i=1,2,⋯,Nξi≥0,i=1,2,⋯,N试求其对偶形式。
根据支持向量机的对偶算法得到对偶形式,由于不能消去变量 ξ i \xi_i ξi的部分,所以拉格朗日因子也包含 μ i \mu_i μi。
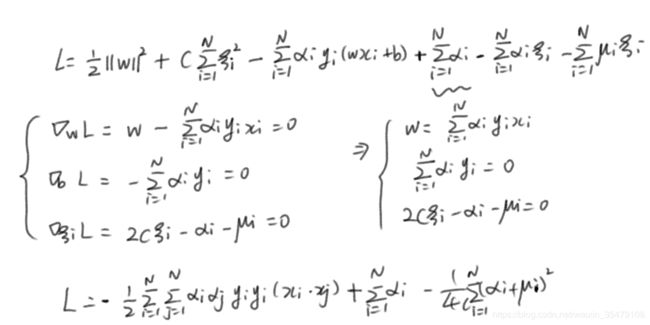
4 证明内积的正整数幂函数 K ( x , z ) = ( x ⋅ z ) p K(x,z)=(x\cdot z)^p K(x,z)=(x⋅z)p是正定核函数,这里 p p p是正整数, x , z ∈ R n x,z\in R^n x,z∈Rn。
根据书中内容需要证明 K ( X , Z ) K(X,Z) K(X,Z)对应的Gram矩阵 K = [ K ( x i , x j ) ] m × n K = [K(x_i,x_j)]_{m\times n} K=[K(xi,xj)]m×n是半正定矩阵。
对任意的 c 1 , c 2 , ⋯ , c m ∈ R c_1,c_2,\cdots,c_m\in R c1,c2,⋯,cm∈R,有
∑ i , j = 1 m c i c j K ( x i , x j ) = ∑ i , j = 1 m c i c j ( x i ⋅ x j ) p = ( ∑ i = 1 m c i x i ) ( ∑ j = 1 m c j x j ) ( x i ⋅ x j ) p − 1 = ∥ ( ∑ i = 1 m c i x i ) ∥ 2 ( x i ⋅ x j ) p − 1 \sum_{i,j=1}^mc_ic_jK(x_i,x_j) = \sum_{i,j=1}^mc_ic_j(x_i\cdot x_j)^p\\=(\sum_{i=1}^mc_ix_i)(\sum_{j=1}^mc_jx_j)(x_i\cdot x_j)^{p-1}\\ =\|(\sum_{i=1}^mc_ix_i)\|^2(x_i\cdot x_j)^{p-1} i,j=1∑mcicjK(xi,xj)=i,j=1∑mcicj(xi⋅xj)p=(i=1∑mcixi)(j=1∑mcjxj)(xi⋅xj)p−1=∥(i=1∑mcixi)∥2(xi⋅xj)p−1因为 p ≥ 1 p\ge1 p≥1,所以 p − 1 ≥ 0 p-1\ge0 p−1≥0,所以 ( x i ⋅ x j ) p − 1 ≥ 0 (x_i\cdot x_j)^{p-1}\ge 0 (xi⋅xj)p−1≥0,所以原始大于等于0,即Gram矩阵半正定,所以正整数的幂函数是正定核函数。