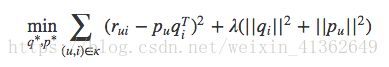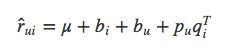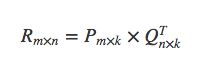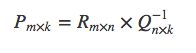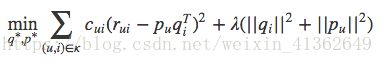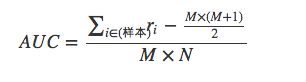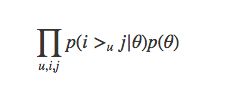推荐系统笔记(矩阵分解)

思维导图：

                    

推荐系统中的经典问题：评分预测(实际应用中，评分数据很难搜集到，属于典型的精英问题)，与之相对的问题是行为预测，处处可见。

矩阵分解

矩阵分解确实可以解决一些近邻模型无法解决的问题，近邻模型存在的问题：1、物品之间存在相关性，信息量并不是随着向量维度增加而线性增加 2、矩阵元素稀疏，计算结果不稳定，增减一个向量维度，导致紧邻结果差异很大的情况出现。

矩阵分解就是把原来的大矩阵，近似的分解成小矩阵的乘积，在实际推荐计算时不再使用大矩阵，而是使用分解得到的两个小矩阵

具体来说就是，假设用户物品的评分矩阵A是m乘n维，即一共有m个用户，n个物品.通过一套算法转化为两个矩阵U和V,矩阵U的维度是m乘k，矩阵V的维度是n乘k。

这两个矩阵的要求就是通过下面这个公式可以复原矩阵A:

                                  

类似这样的计算过程就是矩阵分解，还有一个更常见的名字SVD，但是SVD和矩阵分解不能划等号，因为除了SVD还有一些别的矩阵分解方法。

1、基础的SVD算法

矩阵分解，就是把用户和物品都映射到一个K维空间上，这个k维空间不是直接看到的，通常称为隐因子

每一个物品都得到一个向量q，每一个用户也得到一个向量p。对于物品，与它对应的向量q中的元素，有正有负，代表着这个物品背后暗藏的一些用户关注的因素，对于用户，与它对应的向量p中的元素，也有正有负，代表这个用户在若干因素上的偏好。物品被关注的因素和用户偏好的因素，它们的数量和意义是一致的，就是我们在矩阵分解之处人为指定的k

如何得到每一个用户，每一个物品的k维向量，这是一个机器学习的问题。按照机器学习思想，一般考虑两个要素：1)、损失函数 2)、优化算法

SVD的损失函数是这样定义的：

    

损失函数由两部分组成，前一部分是控制模型的偏差，后一部分控制模型的方差

前一部分：用分解后的矩阵预测分数，要和实际用户评分之间误差越小越好

后一部分：得到的隐因子向量要越简单越好，以控制这个模型的方差，换句话说，让它在真正执行推荐任务时发挥要稳定。

整个SVD的学习过程就是：

      1）准备好用户物品的评分矩阵，每一条评分数据看作是一条训练样本

      2）给分解后的U矩阵和V矩阵随机初始化元素值

      3）用U和V计算预测后的分数

      4)  计算预测的分数和实际的分数误差

      5）按照梯度下降的方向更行U和V中的元素值

      6）重复步骤3到5，直到达到停止条件

得到分解后的矩阵之后，实质上就是得到每个用户和每个物品的隐因子向量，拿着这个向量再做推荐计算更加简单，简单来说就是拿着物品和用户两个向量，计算点积就是推荐分数

2、考虑偏置信息

       有一些用户会给出偏高的评分，有一些物品也会收到偏高的评分，比如一下观众为铁粉的电影，所以原装的SVD就有一个变种：把偏置信息抽出来的SVD

一个用户给一个物品的评分会由四部分相加：

从左到右分别代表：全局平均分、物品的评分偏置、用户的评分偏置、用户和物品之间的兴趣偏好

3、增加历史行为

有的用户评分比较少，事实上相比较沉默的大多数，主动点评电影或者美食的用户是少数，也就是说显示反馈比隐式反馈少。在SVD中结合用户的隐式反馈行为和属性，这套模型称为SVD++，在SVD++目标函数中，只需要把推荐分数预测部分稍做修改，原来的用户向量那部分增加了隐式反馈向量和用户属性向量

学习算法依然不变，只是要学习的参数多了两个向量：x和y。一个是隐式反馈的物品向量，另一个是用户属性的向量，这样在用户没有评分时，也可以用他的隐式反馈和属性做出一定的预测。

4、增加时间因素

在SVD中考虑时间因素，通常有几种做法：1）对评分按照时间加权，让久远的评分更趋近平均值  2）对评分时间划分区间，不同的时间区间内分别学习出隐因子向量，使用时按照区间使用对应的隐因子向量来计算 3）对特殊的期间，如节日、周末等训练对应的隐因子向量

 

Face是如何互相推荐好友

通过之前构建目标函数之后，就要用到优化算法找到能使它最小的参数。优化方法常用的选择有两个，一个是随机梯度下降(SGD)，另一个是交替最小二乘(ALS),在实际应用中，交替最小二乘更常用一些，这也是推荐系统中选择的主要矩阵分解方法

最小二乘原理(ALS)

      找到两个矩阵P和Q，让它们相乘后约等于原矩阵R:

                                   

P和Q两个都是未知的，如果知道其中一个的话，就可以按照代数标准解法求得，比如知道Q，那么P就可以这样算：

                                   

也就是R矩阵乘Q矩阵的逆矩阵就得到了结果，反之，知道了P 再求Q 也一样，交替最小二乘通过迭代的方式解决这个鸡生蛋蛋生鸡的难题：

1)、初始化随机矩阵Q里面的元素值

2)、把Q矩阵当做已知的，直接用线性代数的方法求得矩阵P

3)、得到了矩阵P后，把P当做已知的，故技重施，回去求解矩阵Q

4)、 上面两个过程交替进行，一直到误差可以接受为止

使用交替最小二乘好处：在交替的其中一步，也就是假设已知其中一个矩阵求解另一个时，要优化的参数是很容易并行的；在不是很稀疏的数据集合上，交替最小二乘通常比随机梯度下降要更快的得到结果

隐式反馈：

实际上推荐系统关注的是预测行为，行为就是一再强调的隐式反馈

如何从解决预测问题转向解决预测行为上来，这就是One-Class,简单的理解就是如果把预测用户行为看成一个二分类问题，猜用户会不会做某件事，但实际上收集到的数据只有明确的一类：用户干了某件事，而用户明确不干某件事的数据却没有明确表达，这就是One-Class由来，One-Class数据也是隐式反馈的通常特点。

对隐式反馈的矩阵分解，需要将交替的最小二乘做一些改进，改进后的算法称作加权交替最小二乘，加权交替最小二乘对待隐式反馈：1）如果用户对物品无隐式反馈则认为评分为0；2）如果用户对物品有至少一次隐式反馈则认为评分是1，次数作为该评分的置信度。

目标函数变为：

                      

Cui就是置信度，计算误差时考虑反馈次数，次数越多，就越可信。置信度一般也不是等有反馈次数，根据一些经验，置信度Cui这样计算：

         Cui = 1+aC，a是超参数，需要训练，默认值为40，C是次数

针对那些没有反馈的缺失值，就是在我们给定的设定下，取值为0的评分就非常多，有两个原因需要在实际使用时要注意的问题：1、本身隐式反馈就只有正类别确定的，负类别是假设的  2、会导致正负类别样本非常不均衡，严重倾斜到0评分这边

不能使用所有的缺失值作为负类别，矩阵分解的初心就是要填充这些值。面对这个问题的做法就是负样本采样：挑一部分缺失值作为负类别样本即可，怎么挑有两个方法：1）随机均匀采样和正类别一样多( 试验过不靠谱)  2）按照物品的热门程度采样

推荐计算

让用户和物品的隐因子向量两两相乘实际上复杂度还是很高，尤其是对于用户数量和物品数量都巨大的应用，Facebook提出两个办法得到真正的推荐结果

第一种，利用一些专门设计的数据结构存储所有物品的隐因子向量，从而实现通过一个用户向量可以返回最相似的K个物品

第二种，拿着物品的隐因子向量先做聚类，海量的物品会减少为少量的聚类，然后在逐一计算用户和每个聚类仲系女的推荐分数，给用户推荐物品就变成了给用户推荐物品聚类，得到给用户推荐的聚类后，再从每个聚类中挑选几个物品作为推荐结果。

矩阵分解在推荐系统中的地位非常高，既有协同过滤的血统，又有机器学习的基因，但是尽管如此，传统的矩阵分解无论是在处理显示反馈还是处理隐式反馈都让人颇有微词

矩阵分解的不足

矩阵分解本质上都是在预测用户对一个物品的偏好程度，哪怕不是预测评分，只是预测隐式反馈，也难逃这一个事实。

得到这样的矩阵分解结果后，常常在实际使用时，又是用这个预测结果来排序。所以，从业者们称想要模型的预测误差最小化，结果绕了一大圈最后还是只想要一个好点的排序。

这种针对单个用户对单个物品的偏好程度进行预测，得到结果后再排序的问题，在排序学习中的行话叫做point-wise,其中point意思就是：只单独考虑每个物品，每个物品像是空间中孤立的点一样，与之相对的，还有直接预测物品两两之间相对顺序的问题，就叫做pair－wise

之前说的矩阵分解都属于point-wise模型。这类模型存在的问题是只能收集到正样本，没有负样本，于是认为缺失值就是负样本，再以预测误差为评判标准去使劲逼近这些样本。逼近正样本没问题，但是同时逼近的负样本只是缺失值而已，还不知道真正呈现在用户面前，到底是不喜欢还是喜欢呢？虽然这些模型采取了一些措施来规避这个问题，比如负样本采样，但是尴尬还是存在的，为了排序而绕路也是事实。

更直接的推荐模型应该是：能够较好地为用户排列出更好的物品相对顺序，而非更精确的评分。

针对以上问题提出的方法是：贝叶斯个性化排序，简称BPR模型

贝叶斯个性化排序(BRP模型)

之前用于评价模型预测精准程度的指标是均方根误差。现在关注相对排序，常用的指标是AUC,AUC全称是Area Under Curve，意思是ROC曲线下的面积。

AUC这个值在数学上等价于：模型把关心的那一类样本排在其它样本前面的概率，非常适合用来评价模型的排序效果，比如说，得到一个推荐模型后，按照它计算的分数，能不能把用户真正想消费的物品排在前面？这在模型上线前是可以用日志完全计算出来的

AUC计算步骤：

  1）用模型给样本计算推荐分数，比如样本都是用户和物品这样一对一的，同时还包含了有无反馈的标识

  2）得到打过分的样本，每条样本保留两个信息，第一个是分数，第二个是0或者1，1表示用户消费过，是正样本，0表示没有，是负样本

   3）按照分数对样本重新排序，降序排列

   4）给每一个样本赋一个排序值，第一位r1=n,第二位r2=n-1,以此类推；其中要注意，如果几个样本分数一样，需要将其排序值调整为它们的平均值

   5）最终按照下面这个公式计算就可以得到AUC值

                                  

BPR模型主要做以下几件事情：

1）一个样本构造方法

矩阵分解在训练时候处理的样本是：用户、物品、反馈，这样的三元组形式，其中反馈包含真实反馈和缺失值，缺失值充当的是负样本职责

BRP提出要关心的是物品之间对于用户的相对顺序，于是构造的样本是:用户、物品1、物品2、两个物品的相对顺序，这样的四元组形式，其中两个物品的相对顺序取值是：

           (1) 如果物品1是消费过的，而物品2不是，那么相对顺序取值为1，是正样本 

           (2) 如果物品1和物品2刚好相反，则是负样本

           (3) 样本中不包含其它情况：物品1和物品2都是消费过的，或者都是没消费过的

       这样一来，学习的数据是反应用户偏好的相对顺序，而在使用时，面对的是所有用户还没消费过的物品，这样的物品仍然可以在这样的模型下得到相对顺序

 2）一个模型目标函数

       每条样本包含的是两个物品，样本预测目标是两个物品的相对顺序。按照机器学习的思想，需要考虑目标函数

       BPR根据像交替最小二乘那样完成矩阵分解，先假装矩阵分解结果已经有了，于是就计算出用户对于每个物品的推荐分数，只不过这个推荐分数可能并不满足均方根误差最小，而是满足物品相对排序最佳

       得到了用户和物品的推荐分数后，就可以计算四元组的样本中，物品1和物品2的分数差，这个分数可能是正数，也可能是负数，也可能是0。如果物品1和物品2相对顺序为1，那么希望两者分数之差是个正数，而且越大越好；如果物品1和物品2的相对顺序是0，则希望分数之差是负数，且越小越好

        目标函数：

                

把这个目标函数化简和变形后，和把AUC当成目标函数是非常相似的，也正是因为如此，BPR模型宣称该模型是为AUC而生的

 3）一个模型学习框架

训练方法：一般都采用批量梯度和随机梯度下降两个选择，BRP作者选择一个介于两者之间的训练方法，结合重复抽样的梯度下降，具体步骤如下：1）从全量样本中有放回地随机抽取一部分样本  2）用这部分样本，采用随机梯度下降优化目标函数，更新模型参数 3）重复步骤1，直到满足停止条件

 

小结：传统的矩阵分解，无论是隐式反馈还是显示反馈，都是希望更加精确的预测用户对单个物品的偏好，而实际上，如果能够预测用户对物品之间的相对偏好，则更加符合实际需求的直觉。BRP就是这样一套针对排序的推荐算法，它事实上提出一个优化准则和一个学习框架，至于其中优化的对象是不是矩阵分解并不是它的重点