从图嵌入算法到图神经网络

一、引言

近几年来，伴随着计算机算力的急剧提升，神经网络从历史的尘埃中走出，横扫各大领域，完成一次次颠覆性的创新。依托高度弹性的参数结构，线性与非线性的矩阵变换，神经网络能适用于各式各样的数学场景，在各个类别的应用上我们都能看到神经网络的影子。其中著名的应用方向，包括自然语言处理、计算机视觉、机器学习、生物医疗、推荐系统、自动驾驶等等。图神经网络，广泛应用于社交关系、知识图谱、推荐系统、蛋白质分子建模，同样源自于对传统领域的创新，它的前身是图嵌入算法；而图嵌入算法又以图数据作为载体。这一关系，将贯穿本文始末，成为我们的展开线索。

二、图

在进入图嵌入算法前，本节将详细介绍该领域下的基础知识，包括各类图的概念以及路径相关算法。希望直入主题的读者可直接跳到下一节。

相关概念

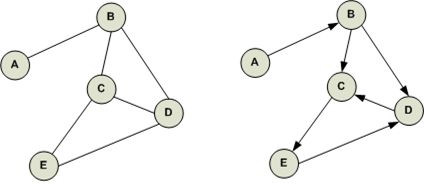
图 (Graph) 是最基础的几种计算机 数据结构 之一，由若干个 节点 (Node, or Vertex) 构成；节点与节点相连，构成 边 (Edge)，代表了两者之间的依赖关系。根据图中边的方向，概念上可将图分为两种：有向图 (Directed Graph, or Digraph) 和 无向图 (Undirected Graph, or Undigraph)，如下所示，左侧为无向图，右侧为有向图：

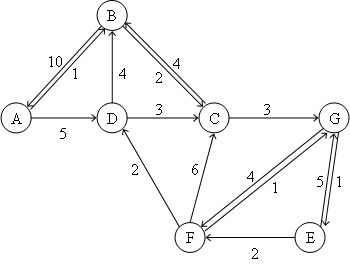
当边被赋予权重，则图可称为 权重图 (Weighted Graph)：

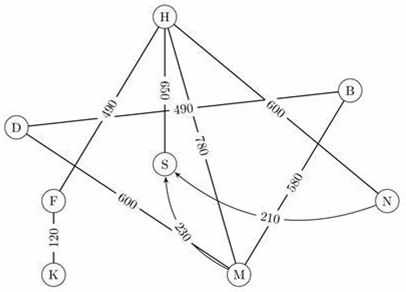
一个形象的例子是城市地图，每一个交叉路口是一个节点，道路是一条边，而权重指的则是道路的长度。但如果我们希望用权重大小代表拥挤程度，在地图上看到每条道路的拥堵情况，那么一条边显然不足以满足我们的要求。这时就引申出了 多重图 (Multigraph)：

概念上，多重图必然是有向图和权重图；但需要注意的是，多重图中两个节点之间的边，既可以单向，也可以双向，i.e. 节点 $A$ 和 $B$ 之间可以有两条或以上 $A\to B$ 的边；两条或两条以上的单向边成为 平行边 (Parallel Edges)，而平行边的数量称为 重数 (Multiplicity)。

此外，还有一些其他类型图的定义，包括 混合图 (Mixed Graph)，指的是既包含无向边也包含有向边的图；连通图 (Connected Graph)，指的是任意两个节点都有路径 (一个或多个边相连) 相连的无向图；强连通图 (Strongly-connected Graph)，指的是任意两个节点都有路径相连的有向图；循环图 (Cyclic Graph)，指的是存在首尾相连的路径，可以串起所有节点的图；以及最后的 完全图 (Complete Graph)，指的是所有节点之间都有边相连的无向图。

清楚这些图的概念，是我们理解算法、熟悉算法应用场景的前提。

路径相关算法

伴随着图一起诞生的，是与路径相关的算法，其中部分算法可以帮助我们从图中提取更多的特征信息融入到节点中，从而丰富图的架构，在图嵌入或图神经网络算法中达到更好的效果。

• 拓扑排序 (Topological Sorting)：
  
  应用于有向非循环图，是对图中的所有节点 $V_i$ $(i=1,...,n)$ 进行统一排序，使得对于任意边 $(V_a\to V_b)$，满足 $a<b$。经过拓扑排序的图，能加速目标检索的效率，同时能够快速获取两个节点间的上下游位置，应用场景包括学位课程之间的先修关系、面对对象程序类之间的继承，以及工程项目之间的调度等。需要注意的是，一个有向非循环图可能存在不止一种拓扑排序的结果。算法原理在于通过迭代，将无入度的节点从原图中抽出放入排序序列中，直至所有节点全部抽出。
• 深度优先搜索 (DFS, abbr. Depth-First Searching)：
  
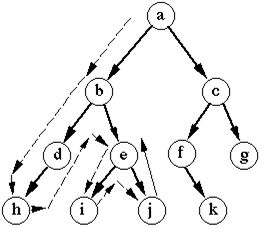
  通过遍历检测两个节点是否连通，或检测一个图是否为连通图。其过程类似于牵着绳子走入迷宫，每一个拐角是一个节点，当走到死角时，记录来过这里，沿着绳子的路线返回寻找下一个拐角；这将用到两个栈，分别记录走访过的节点，以及绳子沿路的拐角。实际应用中，全程只用一根绳子无疑是低效的，因此常常引入递归的思想，每到一个拐点切出多个绳头分头搜索。
• 广度优先搜索 (BFS, abbr. Breadth-First Searching)：
  
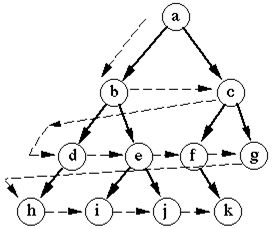
  依据从源点出发，路径上的节点数量，将全图分为不同的层级，逐层向下检查。相对于深度优先搜索，广度优先搜索能够保证在边的数量上两个节点间检索到的路径最短。
• Dijkstra 算法：
  
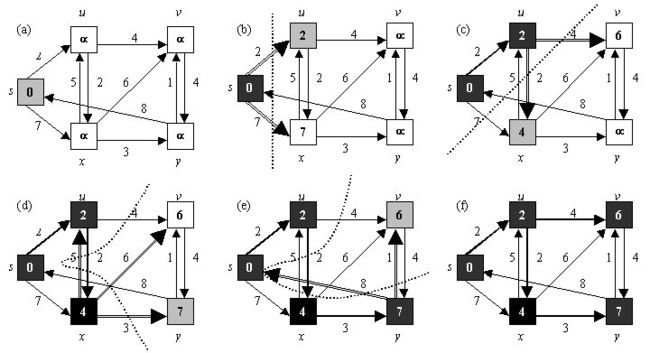
  算法思想在于从源点出发，构建一个逐步扩张的“云”，每次迭代将云外离源点最近的节点拉入到云内来，使云逐渐遍布全图，从而检索到两个节点间的最短路径。时间复杂度为 $O(n^2)$，是贪心算法应用在路径问题上的绝佳案例。
• Floyd-Warshall 算法：
  
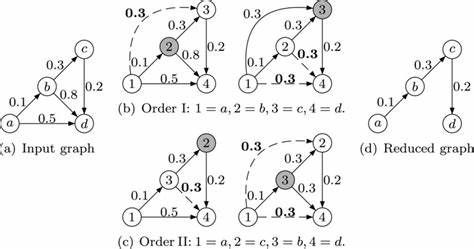
  假如我们不希望每次检索两个节点是否连通，或计算最短路径时，都从头开始遍历，可以使用该算法生成 传递闭包 (Transitive Closure)，以加速后续检索，一劳永逸。该算法的原理在于每次迭代时，将所有满足连通要求的 $V_{k-1}\to V_k\to V_{k+1}$ 的 $V_{k-1}$ 和 $V_{k+1}$ 单独建立联系，构建新的边 $V_{k-1}\to V_{k+1}$。如此一来，多次迭代过后，所有可连通的节点对 ($V_a$,$V_b$) 都将拥有直接关系。需要注意的是，该算法的时间复杂度为 $O(k{n}^3)$，$k$ 为迭代次数，为保证所有可达节点配对存在直接相连的边，算法的运算消耗最高可接近 $O(n^4)$。显而易见，当节点的数量 $n$ 逐渐增加时，算法运行的时间消耗将呈灾难性地增加。
• Prim-Jarnik 算法：
  
  归属于 最小生成树 (MST, abbr. Minimum-Spanning-Tree) 一类的算法，旨在求解连通所有节点的最短路径。由 Dijkstra 算法调整而来，以所有零入度节点作为云的初始状态，不断找寻离云内节点最近的邻点拉入到云内来，以此迭代，直至所有节点访问完毕。如果不存在零入度点，则随机挑选一个加入到云中。

三、图嵌入算法

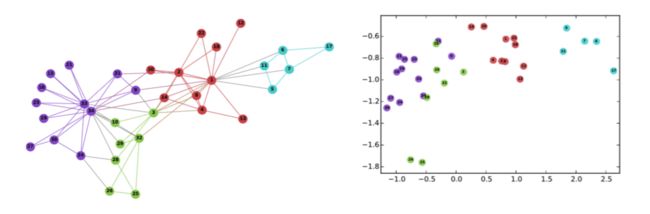
abbr. Graph Embedding Algorithms，目的在于学习图的结构或节点之间的邻接关系，对节点进行编码 (或对固有特征进行降维)，将所有节点映射为等维度的向量，使其能够方便地应用于下游的聚类、分类、关联分析或可视化任务。因此，在实际应用中，图嵌入属于预处理工作，绝大多数图嵌入算法皆为无监督学习算法。

常见概念

• 图 (Graph)：$G(V,E)$
• 节点 (Node, or Vertex)：$V=\{v_1,...,v_n\}$，包含全部节点
• 度 (Degree)：$D=\{de{g}_1,...,de{g}_n\}$，包含每个节点的入度数量
• 边 (Edge)：$E=\{e_{ij}{\}}_{i,j=1}^n$，包含所有的边；如果边是双向的，则分别表达为两条，e.g. $v_i\leftrightarrow v_j$ 关系将对应 $e_{ij}$ 与 $e_{ji}$；如果边 $v_i\to v_j$ 不存在，则不会出现在 $E$ 里面
• 邻点 (Neighbors)：$\mathcal{N}(v_i)$，包含节点 $v_i$ 的所有邻点
• 邻接矩阵 (Adjacency Matrix)：$A=\{w_{ij}|w_{ij}\ge 0{\}}_{i,j=1}^n\in {\mathbb{R}}^{n\times n}$，记录图中边的权重信息；对于无向图，$w_{ij}=w_{ji}$；要求所有的边权重不得小于 0；对于不相邻的节点，$w_{ij}=w_{ji}=0$
• 一阶相似度 (First-order Proximity)：边的权重 $w_{ij}$，代表两个节点的直接依赖关系
• 二阶相似度 (Second-order Proximity)：对于节点 $v_i$ 和 $v_j$，从邻接矩阵分别获取相应的一阶相似性 ${\mathrm{w}}_{\mathrm{i}}=[w_{i1},...,w_{in}]$，${\mathrm{s}}_{\mathrm{j}}=[w_{j1},...,w_{jn}]$；${\mathrm{w}}_{\mathrm{i}}$ 与 ${\mathrm{w}}_{\mathrm{j}}$ 的相似度即为二阶相似度，代表两个节点的邻居相似性
• 图嵌入 (Graph Embedding)：映射关系 $f:v_i\to z_i\in {\mathbb{R}}^d,\forall i\in [1,n]$，$d$ 为超参数，决定最终的编码长度
• 特征表示 (Feature Representation)：$X_i\in {\mathbb{R}}^{d_0}$，对节点 $v_i$ 的固有特征 (不包含边及其他节点信息) 进行简单编码后形成的向量，因此又称为特征向量

演变历程

图嵌入算法初步诞生于 21 世纪初，彼时的模型将更多的焦点放在降维上，嵌入的同时使得相邻的节点在最终的向量空间上更为接近，代表性的包括 Locally Linear Embedding (2000) 和 Laplacian Eigenmaps (2001) ，这一类算法充分利用所有的样本间权重，时间复杂度通常较高，最高可达 $O(n^2)$，因此并不适合大规模图数据。2010 年以后，新诞生的图嵌入算法逐渐在时间复杂度上得到优化，转而应对现实生活中广泛存在的特征稀疏性问题，这其中的翘楚便是 Graph Factorization (2013)，该算法旨在于邻接矩阵以及正则项之间寻求一个平衡点，使得生成的向量保留邻接矩阵的绝大多数信息；LINE (2015) 将该思想延续下去，并努力在嵌入向量中维持节点的一阶和二阶相似度；HOPE (2016) 更是引入了更高阶的相似度矩阵，通过广义奇异值分解保留高阶相似性。以上所有算法皆可归类于矩阵分解，又称为因子分解，其中心思想在于生成相似度矩阵，通过数学方法将矩阵中包含的邻接信息融入节点向量中。

另一个知名的流派是基于随机游走，以 DeepWalk (2014) 和 node2vec (2016) 作为代表。前者在节点的上下游随机走动，生成长度为 $2k+1$ 的等长序列，作为节点的邻接特征导入 skip-gram 模型训练；后者在前者的基础上对随机游走在 DFS 和 BFS 的方向上施加权重，使生成的序列更为真实地体现节点的结构信息。

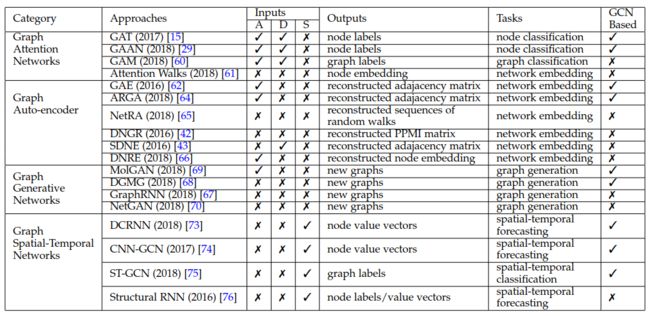
在这之后，图嵌入算法逐渐过渡到神经网络时代，涌现出一大批优质的图神经网络模型，包括 SDNE (2016) 与 GraphSAGE (2017) 等等，在工业界大放异彩。从此，基于神经网络的图嵌入算法不再仅仅局限于节点的邻接信息，而开始将节点本身的特征纳入模型考量，并逐渐从静态的直推式 (transductive) 学习向动态的归纳式 (inductive) 学习演变，无论是拟合能力还是泛化能力，都大大提升；部分图神经网络直接针对下游任务进行建模，已不再属于图嵌入的范畴。依据 Wu et. al (2019) 的定义，图神经网络可分为五大类：

• 图卷积网络 (Graph Convolution Networks)：简称为 GCN，是目前最主流的图神经网络算法，其余四种图神经网络皆由 GCN 演化而来。依据建模过程中是否应用到傅里叶变换，可将其分为基于谱 (Spectral-based) 和基于空间 (Spatial-based) 两个流派。
• 图注意力网络 (Graph Attention Networks)：引入注意力机制，将图网络整合为端到端的模型；具体的做法，是在 GCN 的聚合函数中加入可训练的权重参数，使得训练后的模型将更多的重心放在关键的邻点上。
• 图自编码器 (Graph Auto-encoders)：由一个编码器 (encoder) 和一个解码器 (decorder) 构成；在应对无固有特征的图时，编码器对邻接矩阵进行一定的预处理，包括融入更丰富的邻接信息 (e.g. 高阶相似度) 或是将邻接矩阵输入一套神经网络；在应对包含固有特征的图时，则直接使用 GCN 作为编码器对邻接矩阵进行编码；解码器对编码结果进行后续处理获得一阶及二阶相似度，通过计算损失函数对模型参数进行更新。
• 图生成网络 (Graph Generative Networks)：2018 年以后出现的新的研究方向，目的是在图的节点和边经验分布的基础上，生成新的图，进行对抗式训练。
• 图时空网络 (Graph Spatial-Temporal Network)：旨在于时空图中学习模式 (pattern)，应用在分类或是对未来特征的预测。

GNNPapers 详细列示了图神经网络诞生以来里程碑式的优秀模型，以及其在具体场景中的应用。

四、图卷积网络

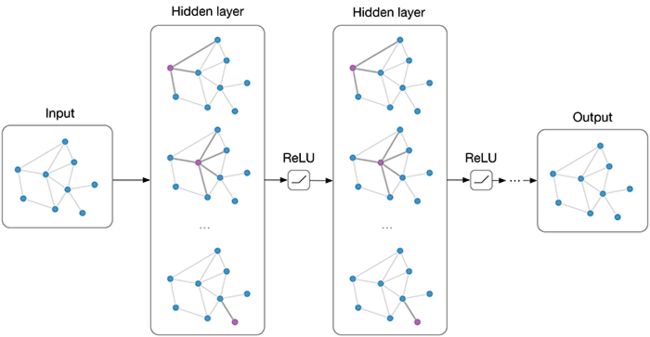
abbr. Graph Convolution Networks。在节点嵌入这一下游任务上，基于空间的 GCNs 从彼时大热的卷积神经网络中汲取思想，直接在原图的拓扑序列上进行卷积操作；而考虑到图结构的不稳定性，基于谱的 GCNs 则将所有节点映射到傅里叶域后进行卷积乘积，再经由傅里叶逆变换得到空间域下的嵌入向量。以下是 Wu et. al (2019) 对近年来图卷积网络的总结：

GNN: The Graph Neural Network Model (2009)

论文地址：https://ieeexplore.ieee.org/document/4700287

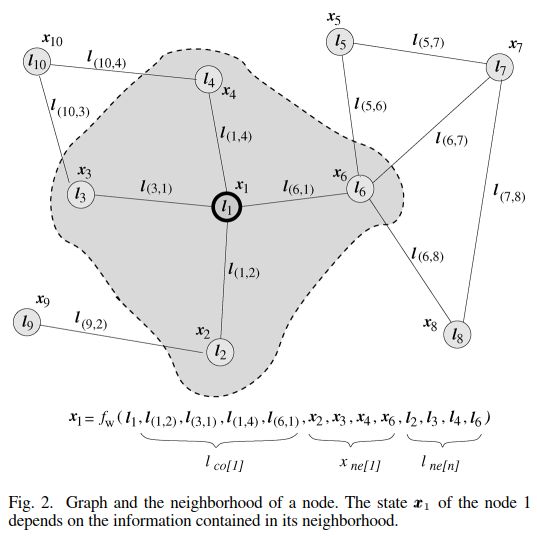
这篇论文首次提出图神经网络 (Graph Neural Network) 的概念，并将模型设计为有目的的监督学习模型，分为 转换 (Transition) 和 输出 (Output) 两个部分。转换部分为每一个节点提取邻点信息，生成向量表示的 状态 (state)；输出则将该状态映射至等维的向量表示，通过 softmax 归一化进行多分类预测。相关公式如下：
$$x_n=f_w(l_n,l_{co[n]},x_{ne[n]},l_{ne[n]})$$$$o_n=g_w(x_n,l_n)$$

其中 $f$ 和 $g$ 皆为可训练的全连接层，$l_n$ 为节点的标签 (可以理解为特征)，$l_{co}$ 为与节点相接的边的标签 (即我们常谈的权重)，$x_{ne}$ 代表邻点转换过后的状态 (向量)，$l_{ne}$ 为邻点的标签 (特征)。由于转换部分的输入 $x_n$ 包含了该部分邻点的输出，因而需要通过交互性的多轮迭代实现训练和推理，论文中将其称呼为 扩散机制 (Diffusion Mechanism)：

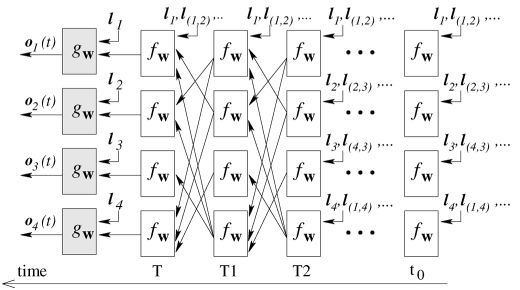
相关的数学定理 Banach’s Theorm 证实，经过扩散机制后，对于满足 $||f_w(x,l)-f_w(y,l)||\le \mu ||x-y||,0\le \mu <1$ 的 $w$，有仅有唯一的解。因而在训练完成后，我们可以提取 $f_w(x,l)$ 作为节点的嵌入表示。

该模型除了可用于节点级别的分类，同样可用于图的级别，只需要为每张输入的图添加一个代表全局的特殊节点即可。由于模型应用到了在节点级别进行邻点采样作为输入的思想，与后来的图卷积神经网络不谋而合，论文作者虽没有自行提出卷积的概念，但本篇论文后来被认为是第一个图卷积网络的提出者。模型采用顺时针的方式为每个节点提取固定长度的邻点列表，对相对位置上空缺的邻点采取统一的无意义填充策略；这样的做法将算法的应用场景限制在了 2D 空间，且需要使用者进行更为繁琐的数据预处理，因而成为饱受诟病的之处，也为后续优化指引了方向。

GraphSAGE: Inductive Representation Learning on Large Graphs (2017)

论文链接：https://arxiv.org/abs/1706.02216

初代 GNN 中邻点采样的思想一直保留了下来，但 GraphSAGE 并不将采样信息局限在节点的拓扑结构里，而是使用节点的固有特征取而代之，对造成庞大参数量的扩散机制也选择了摒弃处理。根据下游任务的不同，GraphSAGE 采用不同的训练策略：应用于图嵌入时，使用负采样技术计算二阶相似度实现参数收敛；应用于分类任务时，使用 softmax 进行有监督学习。其中，无监督学习的表达式如下：
$${\mathcal{J}}_{\mathcal{G}}(z_u)=-\log (\sigma (z_u^T{z}_v))-Q\cdot {\mathbb{E}}_{v_n\sim P_n(v)}\log (\sigma (-z_u^T{z}_{v_n}))$$

模型的特别之处，在于每一次迭代时，都重新对邻点进行采样，前馈公式如下：
$$h_v^k=\sigma (W^k\cdot \text{Concat}(h_v^{k-1},h_{\mathcal{N}(v)}^k))$$$$h_{\mathcal{N}(v)}^k=\text{Aggregate}(\{h_u^{k-1},\forall u\in \mathcal{N}(v)\})$$

其中 $k=1,...,K$ 为迭代次数；$h_v^k$ 为前馈层输出的隐藏向量，无监督学习使用最后一层计算损失函数。

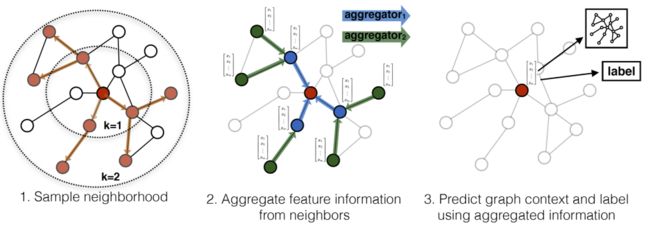
邻点采样的方法为设置固定的窗口大小，不足或过剩都采用随机的方式进行选取；采样完毕后使用聚合函数将邻点的隐藏向量聚合为一个等长的向量表示。论文中提出了三种聚合策略：

• 均值聚合 (MeanAggregator)：直接对所有邻点 (包括自身) 的隐藏向量求均值；
  $$\text{Concat}(h_v^{k-1},h_{\mathcal{N}(v)}^k)=\text{Mean}(\{h_v^{k-1}\}\cup \{h_u^{k-1},\forall u\in \mathcal{N}(v)\})$$
• LSTM 聚合 (LSTMAggregator)：利用 LSTM 在时序信息处理上的优势，将采样得到的邻点序列打乱后依次输入 LSTM 中，取隐藏状态与节点本身的隐藏向量进行纵向合并；
  $$h_{\mathcal{N}(v)}^k=\text{LSTM}(\{h_u^{k-1},\forall u\in \mathcal{N}(v)\})$$
• 池化聚合 (PoolingAggregator)：引入包含可训练参数的全连接层对每一个邻点的向量进行处理，将最后的输出进行最大池化；
  $$h_{\mathcal{N}(v)}^k=\text{Max}(\{\sigma (W_{pool}{h}_{u_i}^k+b),\forall u_i\in \mathcal{N}(v)\})$$

GraphSAGE 第一次提出使用 归纳式 (inductive) 的图神经网络代替 直推式 (transductive) 的旧模型，以提高其在实际应用中的效率；然而，其虽能够通过推理直接得出训练样本外节点的输出，但本质上无法在推理的同时进行参数的更新。这一问题引发了动态图的研究工作，至今依然是最为热门的方向。

Spectral CNN: Spectral Networks and Locally Connected Networks on Graphs (2014)

论文地址：https://arxiv.org/abs/1312.6203

在有向图中，由于每个节点的邻点数目并不固定，因而直接在空间上对节点进行卷积操作难免与真实的分布形成差异，导致模型效果受阻。基于谱的图卷积网络能有效解决这一类问题。模型的思路在于仿照 CNN，分为多层进行前馈；每一层使用不同的卷积核在傅里叶域进行卷积，同时在得到空间域的表达后对其使用 max pooling 进行聚合。图的拉普拉斯矩阵可以通过两种常见的方式计算：未标准化的 $L=D-W$，以及标准化的 $L=I-D^{-1/2}W{D}^{-1/2}$。在对 $L$ 进行特征分解后，第 $k$ 个卷积层的公式定义如下：
$$x_{k+1,j}=h\left(V\sum _{i=1}^{f_{k-1}}{F}_{k,i,j}{V}^T{x}_{k,i}\right)(j=1,...,f_k)$$

其中 $f_k$ 为该层卷积核的数量；$V$ 为 $L$ 的特征向量；$F$ 为包含训练参数的对角矩阵；$h$ 为非线性激活函数。卷积核的数量逐层减少，卷积层后外接一个全连接层，实现输出。

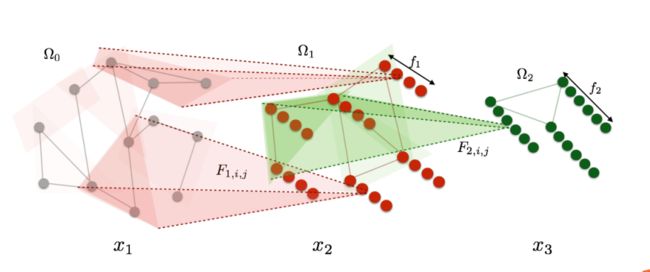
模型的优点是显而易见的，相比于基于空间的图卷积网络，无需进行邻点采样；相对于传统图模型，通过多层卷积大大提升特征提取能力。缺点是谱卷积在计算过程中需要对图的拉普拉斯矩阵进行特征分解，时间复杂度最高可达 $O(n^3)$，无疑是灾难性的。该模型提出后，谱卷积很快便通过切比雪夫多项式实现了优化。

ChebNet: Semi-supervised classification with graph convolutional networks (2016)

论文链接：https://arxiv.org/abs/1609.02907

泛化至节点的分类和嵌入任务上，该论文提出的半监督式 GCN 在许多下游任务榜单中实现了最优成绩，并因此迅速蹿红。卷积层的前馈公式如下：
$$H^{l+1}=\sigma \left({\tilde{D}}^{\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^{(l)}{W}^{(l)}\right)$$$$\tilde{A}=A+I_N$$

其中 $\tilde{A}\in {\mathbb{R}}^{N\times N}$ 为添加了自连接关系的邻接矩阵，$\tilde{D}$ 为度矩阵，$W$ 为可训练参数，$H$ 为卷积层的输出。为了在模型参数中引入无标签节点的信息，模型在损失函数中引入了正则项：
$$\mathcal{L}={\mathcal{L}}_0+{\mathcal{L}}_{reg},\text{with}{\mathcal{L}}_{reg}=\sum _{i,j}{A}_{i,j}||f(X_i)-f(X_j)|{|}^2=f(X{)}^T\Delta f(X)$$

其中 ${\mathcal{L}}_0$ 为监督学习损失，$\Delta =D-A$ 为未标准化的拉普拉斯矩阵。

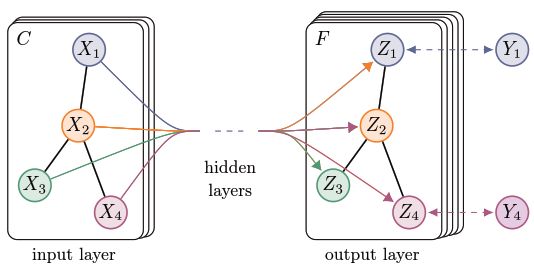
模型的一大贡献在于通过设定感受野宽度为 1，并增加模型深度，来对前代基于切比雪夫多项式的谱卷积进行进一步优化；其余优点自不用再提，缺陷在于训练时并未对原始输入进行压缩，端对端地对整张图进行处理。尽管模型已进行优化，但层数的增加依然使其耗时过长。为此，后续的优化主要以加速训练为主，e.g. 在每一层进行采样计算。

五、其他

图注意力网络

abbr. Graph Attention Networks。Attention 机制自 Google 于 2014 年提出后便广泛应用于序列建模任务中，尤其在自然语言处理领域。应用于图神经网络，Attention 机制有两种用法，第一种是用在邻点序列的生成上，第二种是用在邻点向量的聚合上；两种方法都使得模型将更多的焦点放在有重要相似度的两个邻点上。由于 Attention 机制的思想在各个领域都是共通的，在展开论文之前我们先对其进行一定的介绍。Attention 机制的核心在于三个要素：Query, Key 和 Value，公式如下，
$$\text{Attention}(Q,K,V)=\text{softmax}(\frac{Q{K}^T}{\sqrt{d_k}})V$$

其中分母的 $d_k$ 为缩放的维度，默认为 1。通过点积计算 Query 和 Key 的相似度，将相似度结果作为权重对 Value 进行加总，这便是最常见的 Attention 形式。在此基础上进行变形，将 Query, Key, Value 经过多组线性变换后分别进行独立的 Attention 计算，对得出的结果进行合并，这样的 Attention 机制称为 Multi-Head Attention：
$$\text{MultiHead}(Q,K,V)=\text{Concat}(hea{d}_1,...,hea{d}_h)$$

$$hea{d}_i=\text{Attention}(Q{W}_i^Q,K{W}_i^K,V{W}_i^V)$$

除以上两者之外，Attention 还有诸多不同的变形方式，包括拼接后导入感知机代替点积进行相似度计算，以及以加权平均的方式代替 Attention 输出特征与 Query 的纵向合并；由于图神经网络中涉及不多，在这里不进行赘述。于 2017 年至 2018 年先后诞生的几个图注意力网络中，GAT (2017) 将 Multi-head Attention 机制用在邻点的聚合上，相似的邻点获得更大的聚合权重；
$$h_i^t=|{|}_{k=1}^K\sigma (\sum _{j\in {\mathcal{N}}_i}\text{MultiHead}(h_i^{t-1},h_j^{t-1})W_k^{t-1}{h}_j^{t-1})$$

GAAN (2018) 将 GAT 中多个注意力头的输出从拼接改为加权平均；
$$h_i^t={\varphi }_o(x_i\oplus |{|}_{k=1}^K{g}_i^k\sum _{j\in {\mathcal{N}}_i}\text{MultiHead}(h_i^{t-1},h_j^{t-1}){\varphi }_v(h_j^{t-1}))$$

其中 $\varphi$ 为全连接前馈层；Attention Walks (2018) 将 Attention 思想应用于 DeepWalks，为共现矩阵附加权重，影响随机游走的方向。由于 Attention 组块无法自行训练，在模型流程中引入 Attention 机制后，必须将其设置为端到端的模型，因而图注意力网络的训练通常是有监督的。

图自编码器

abbr. Graph Auto-encoders，在 GCNs 的基础上，将任务专注于图嵌入，不再进行特定的分类任务。GAE 的共性在于使用 encoder 得到潜在向量，并以 decoder 判断潜在向量中包含的相似度信息是否与相似度矩阵保持一致。decoder 通常为全连接层；而 encoder 则以 MLP 或 GCN 为主流，一些变形包括接入 Attention 机制，或直接以 LSTM+Attention 作为编码器。以第一代图自编码器 GAE (2016) 为例，GAE 应用 GCN 作为编码器，通过重构邻接矩阵，在一阶相似度的层面拟合模型：
$$Z=\text{GCN}(X,A)$$$$\hat{A}=\sigma (Z{Z}^T)$$

但基于一阶相似度的模型无法应对现实生活中广泛存在的高度稀疏的数据，因而 SDNE (2017) 在有监督的一阶相似度基础上，在损失函数中引入二阶相似度，以期完整地保留图的结构信息：
$$L_{1st}=\sum _{i,j=1}^n{A}_{i,j}||h_i^{(k)}-h_j^{(k)}|{|}^2$$$$L_{2nd}=\sum _{i=1}^n||({\hat{x}}_i-x_i)\odot b_i|{|}^2$$$$L_{reg}=\frac{1}{2}\sum _{k=1}^K(||W^{(k)}|{|}_F^2+||{\hat{W}}^{(k)}|{|}_F^2)$$$$L={\lambda }_1{L}_{1st}+L_{2nd}+{\lambda }_2{L}_{reg}$$

其中 $h_i^{(k)}$ 为 encoder 的输出；$\widehat{x_i}$ 为 $h_i^{(k)}$ 经过 decoder 得到的重构输入向量；$b_i=1\text{if}{A}_{i,j}=0\text{else}\beta (\beta >1)$，用于对既有邻接信息施加更大的惩罚；$L_{reg}$ 为基于 L2 范数的模型正则项。SDNE 的 encoder 和 decoder 皆为多层感知机架构。图自编码器的主要困难在于如何应对高度稀疏的邻接矩阵，出于 SDNE 在该问题上出色的应对能力，SDNE 得以成为目前最为出色的图嵌入算法之一。

图生成网络

abbr. Graph Generative Networks。相对于其他分支而言，图生成网络的应用场景较少，主要包括生物医药和工程学等领域。目前存在的 GGNs 差异较大，鲜有继承关系，但根据模型特质可分为两类：一类基于构建生成器 (generator) 和判别器 (discriminator) 进行对抗式训练，这里的思路和计算机视觉领域的 GAN 是保持一致的；另一类则在于得到既有的图数据分布，而后给定一定信息，在满足该分布的前提下交替式地生成节点和边，逐渐扩展至全图。

MolGAN (2018) 便是基于第一类思路，将生成网络应用在合成化学领域，同时应用了 GCN、对抗式生成网络以及强化学习的原理。MolGAN 的模型结构分为三个部分：生成器 $G_{\theta }$、判别器 $D_{\theta }$，以及奖励网络 ${\hat{R}}_{\psi }$。生成器在参数的基础上生成完整的图结构，与样本数据共同导入判别器中；判别器辨识真假，激励生成器生成符合样本图分布的新图；奖励网络在判别器运作的同时，对图的真实性和合理性进行评分，避免生成器生成不具备现实意义的图。

GraphRNN (2018) 则遵循第二类思路，采用双层循环神经网络设计，第一层基于图的级别处理隐藏状态，为节点序列添加新的节点；第二层则基于边的级别生成布尔值列表，判断新生成的节点与原序列中的节点是否存在邻接关系。训练前通过广度优先搜索，将图数据平铺为节点序列导入模型中，相关表达式为：$$p(G)=\sum _{S^{\pi }}p(S^{\pi })\mathbb{I}[f_G(S)=G]$$

其中 $f_G$ 表示从序列到图的映射关系；对于无向图，$S^{\pi }$ 决定了唯一的图结构。相对于基于对抗式训练的生成式模型，GraphRNN 的优势在于能够同时保留原图信息，并高效地生成几乎任意长度的图。

图时空网络

abbr. Graph Spatial-temporal Networks，专门用于处理时空图数据。时空图与我们常说的图主要区别在于，时空图的节点和边的特征处在实时变化中，e.g. 城市的交通路况。而图时空网络主要应用在两种下游任务中：分类以及预测未来特征。在建模过程中，图时空网络将节点与节点的依赖关系分为空间依赖关系 (spatial dependencies) 和临时依赖关系 (temporal dependencies)。

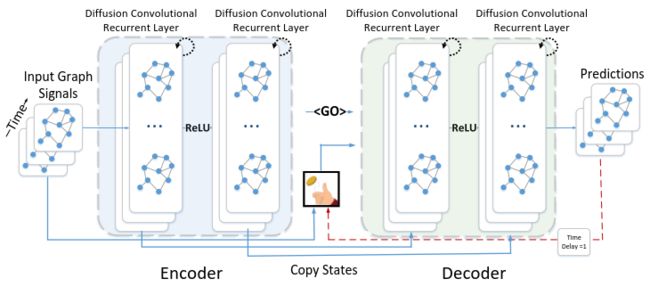
预测未来特征的端到端模型 DCRNN (2017) 使用扩散卷积 (diffusion convolution) 来捕捉空间依赖关系，而使用基于 GRU (Gated Recurrent Unit) 的 seq2seq 架构捕捉临时依赖关系。更为直观的表达方式是，在同一个时空的内部节点之间进行卷积，而在同一个节点的不同时空状态使用 seq2seq。

模型节点序列的生成基于随机游走，每走访一个节点，以 $\alpha \in [0,1]$ 的概率重新开始新的序列；而扩散卷积的过程中对每一条序列进行双向处理。第 $p$ 个卷积核的相关表达式：
$${\mathbf{X}}_{:,p\star \mathcal{G}}{f}_{\theta }=\sum _{k=0}^{K-1}({\theta }_{k,1}(D_O^{-1}W{)}^k+{\theta }_{k,2}(D_I^{-1}{W}^{\mathcal{T}}{)}^k)X_{:,p}\text{for }p\in \{1,...,P\}$$

其中，$\theta \in {\mathbb{R}}^{K\times 2}$ 为卷积核表达式；$D_O^{-1}W$ 和 $D_I^{-1}{W}^{\mathcal{T}}$ 分别为出度转移矩阵及入度转移矩阵。由于涉及庞大的计算量，DCRNN 的运算效率其实并不高，后续的优化中，CNN-GCN (2018) 使用 1D CNN 代替扩散卷积，使得运行效率大大提高。

六、总结

图神经网络相对于传统的卷积神经网络和循环神经网络的不同之处，在于其高度的可塑性和多样性。例如，有不同的卷积策略、不同的采样策略、不同的相似度矩阵/邻接矩阵计算方式，任何一个环节的改变都会对最终的模型效果产生质的区别，因而难有适用于大面积场景的高泛化性明星模型的出现。在实践中，应当依据明确的场景需求来设计网络。以下呈现笔者总结的模型择优策略，供读者参考：

【1】任务目的：图分类【2】、节点分类【3】、节点嵌入【4】、关系预测【15】
【2】数据规模：大型【9】、小型【10】
【3】数据规模：大型【5】、小型【7】
【4】使用邻接矩阵或是使用节点的固有特征：邻接矩阵【14】、节点特征【13】
【5】使用邻接矩阵或是使用节点的固有特征：邻接矩阵【6】、节点特征【13】
【6】邻接矩阵是否稀疏：是【11】、否【12】
【7】使用邻接矩阵或是使用节点的固有特征：邻接矩阵【8】、节点特征【13】
【8】使用能进行节点级别分类任务的 <基于谱的图卷积网络>, e.g. 1stChebNet
【9】使用能进行图级别分类任务的 <基于空间的图卷积网络>，e.g. PATCHY-SAN, DCNN
【10】使用能进行图级别分类任务的 <基于谱的图卷积网络>，e.g. Spectral CNN, ChebNet
【11】使用 SDNE 等高效应对稀疏数据的 <基于空间的图自编码器> 对节点进行编码后进入【13】
【12】使用能进行节点级别分类任务的 <基于空间的图卷积网络>，e.g. DCNN
【13】使用 GraphSAGE
【14】数据规模：大型【15】、小型【16】
【15】使用 SDNE
【16】使用 <传统图嵌入算法>，e.g. HOPE, node2vec

出于 GraphSAGE 和 SDNE 的一些优秀特性，笔者在部分场景里优先推荐使用；此处没有提到图注意力网络，是由于注意力机制作为一种建模思想，几乎可以应用于任何以分类作为下游任务的图神经网络，而并非现在既有的应用了注意力机制的示范模型；没有提到图生成网络和图时空网络是由于其应用场景较为局限，目的也更为明确。

七、前沿探索

本文呈现的皆为 2018 年及以前，经受住实践考验的经典图神经网络。依据 2019 年以后发布的论文，前沿研究主要关注以下几个方面：

• 动态图 (dynamic graph)：目前绝大多数图嵌入算法和图神经网络都是静态的、直推式的，当我们引入新的节点，希望预测节点的分类或为其进行嵌入时，e.g. 新注册用户的加入，需要将整张图重新进行训练，这无疑相当低效。针对动态图的研究期望能解决这一类问题。
• 异质图 (heterogeneous graph)：将图神经网络应用在知识图谱等领域时需要面对的问题 —— 节点和边可能不只一类。如何为这样的图进行节点嵌入，HAN (2019) 提供的解决方案是将隐藏向量的聚合分为两步进行。
• 边的特征：传统图嵌入算法仅利用了边的权重信息，GraphSAGE 引入了节点的固定特征，下一步有研究者将注意力放在如何将前两者与边的特征结合上。

References

[1] Palash Goyal, E. F. (2017). Graph Embedding Techniques, Applications, and Performance: A Survey. Retrieved from https://arxiv.org/abs/1705.02801
[2] Zonghan Wu, S. P. (2019). A Comprehensive Survey on Graph Neural Networks. Retrieved from https://arxiv.org/abs/1901.00596