no1 计算机视觉历史 & k近邻线性分类器 & 损失函数和最优化

计算机视觉历史回顾和介绍

现代互联网85%都是图片，如何处理？计算机视觉十分必要。

哈佛大学放图片对猫的脑部视觉区脉冲检测，50%都在处理眼睛的信息，发现切换图片的时候才有感觉，所以视觉的前期是对图片边缘和形状的识别。

Block world论文，一个东西不同角度，边缘决定形状和结构，可以通过边缘和形状来识别东西。

1966年MIT建立了第一个AI实验室，在那个夏天研究了计算机视觉。

David Marr提出视觉是分层的。

1. 从简单的形状开始处理
2. 建立一个分层的模型，第一层应该是边缘

早期的计算机视觉，70年代，其一认为物体都是由基本的形状构成的，比如说圆柱形，其二，由基本的组件构成，比如说鼻子等，可以容许形变。3D建模。

80年代处理彩色图像，以及图像分割，或者说normalized cut，和感知分组。实时人脸检测和特征。

从70到80，从3D建模到识别，从计算机视觉到人工智能。

数据驱动的图像分类方式：K近邻和线性分类器

难度：比如说猫图片的分类，形状不一、种类不同、有遮盖、光线不好的图片都能够分类出来

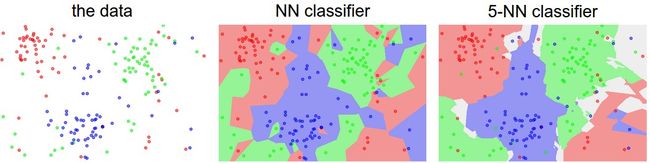
K近邻

数据集：CIFAR-10，其中有50000张训练图片和10000张测试图片，10中标签，图片大小为32*32*3

方法：对于一张图片，和训练图片依次比较，找到距离最近的一张图片，该图片的标签就是我们需要分类的图片的标签。对于k>1的情况，在训练集中找到前k个距离最近的图片，然后投票表决。

距离定义：

1. L1距离（manhattan distance）

d1(I1,I2)=∑P|IP1−IP2|

图片大小相同，对应元素依次相减取绝对值，得到一个相同大小的矩阵，将该矩阵的元素求和最后得到的值就是这两张图的L1距离。
2. L2距离（Euclidean distance）

d2(I1,I2)=∑P(IP1−IP2)2−−−−−−−−−−−√

问题：

1. 因为每个图片的分类都要依次和训练集比较，因此算法复杂度随着训练集规模的扩大成线性增长
2. 效果不好，实际中很少使用，比如说对于同一张图片，要是有一点偏移或者色调发生了变化，距离就会变化很大

主要超参数：
1. k，和几个图片进行比较
2. distance，使用L1距离还似乎L2距离

可以看到随着k的增加，对异常点的处理越好，可以增加模型的泛化能力。

如果数据量比较小，可以通过交叉验证来得到模型分类能力的评估。5折交叉验证，把数据集分成5份，依次挑选其中的1份作为验证集，剩下的作为训练集，最后在验证集上分别得到5个分数，取平均就是该参数下模型的分数。

优点和缺点：

1. 算法简单易于实现
2. 训练不需要时间，但是预测耗时长，对实际使用不利
3. 在图像分类问题上效果不好，肉眼不可见的平移颜色等，都会导致距离变得很大

线性分类器

总览：一个分类模型由两个函数和一个方法组成，第一是通过输入数据得到各个分类的得分，第二是通过模型预测和实际值得到损失，方法是通过调整第一个函数的权值来减少第二个函数输出的损失。

参数方法和非参数方法

• 参数方法，比如说线性分类器，通过学习训练集，来改变模型的参数w和
  b
• 非参数方法，比如说k近邻，没有需要学习的参数

Score Function

首先定义线性分类器的第一个函数，通过输入数据来得到分类的得分。

f(xi,W,b)=Wxi+b

其中 xi 是(D,1)的向量，代表输入数据的一个样本，D是特征数，W是(K,D)的矩阵，代表权重其中K是分类数，b是偏置向量，输出y是一个(K,1)的向量，代表该样本在各个类上的得分。

对三个通道的颜色值进行加权求和，再加上偏置，返回一个向量，每个值表示各个标签的得分。

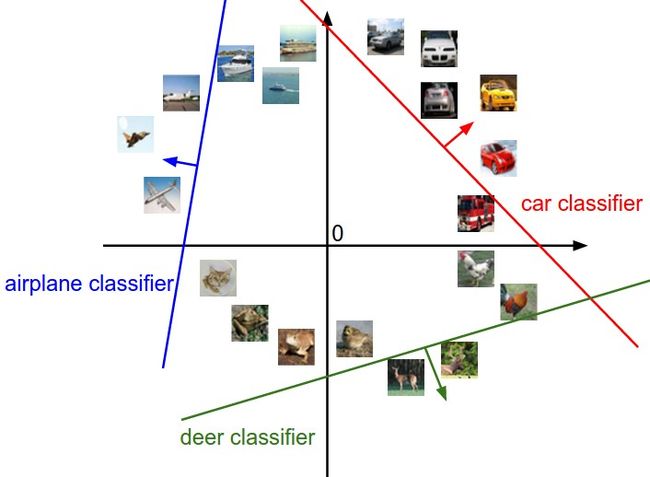
可以把一张图片中的3072（三通道乘上每个像素点）看成是3072维的数据，拟合了3条“直线”，对3个标签计算得分。

每一行的W都是一个分类器。

去均值化：

1. 对于前面的k近邻来说，不需要去均值，因为图片的像素是在同一个尺度，或者说同一个量纲下
2. 而对于如上的线性分类器来说，如果去均值，就可以在参数中去掉偏置b

Loss Function

损失函数是用来量化模型输出预测和实际值的差距，用来衡量模型预测能力的好坏，在如上的模型中，就是为了评估分类器（权重W）的好坏。

多分类SVM损失(hinge loss)

给定一个样本( xi,yi )，其中x是一个图片，y是一个标签，然后使用 s=f(xi,W) 来计算分数向量。

最后得到SVM损失，对于一个样本的loss： Li=∑j≠yimax(0,sj−syi+Δ) ，其中 Δ 可以是任意一个大于0的数，一般取1，因为线性W可以成比例的调整。该值代表一段距离，不加这项，计算错误分类得分比实际分类分数高部分的损失，加上这个，计算那些错误分类得分比实际分类高的，以及接近实际分类分数的损失。

例子:

	a cat image	a car image	a frog image
cat	3.2	1.3	2.2
car	5.1	4.9	2.5
frog	-1.7	2.0	-3.1
Losses	2.9	0	10.9

L1==max(0,5.1−3.2+1)+max(0,−1.7−3.2+1)max(0,2.9)+max(0,−3.9)=2.9+0=2.9

整个训练集的损失为： L=1N∑Ni=1Li

在这个例子中，L=(2.9+0+10.9)/3=4.6

正则化

对于一个数据集，如果存在一组权重W，能使损失为0，那么一定也存在很多W，能使损失为0，比如说正比例的W。那么如何能从这个解空间中挑出比较好的W，就需要正则化操作。使用了正则化项，可以提高模型的泛化能力，也就是提高模型在测试集上的性能。

L=1N∑i∑j≠yi[max(0,f(xi;W)j−f(xi;W)yi+Δ)]+λ∑k∑lW2k,l

通常有如下的正则化项：

名称	R(W)
L2正则化	∑k∑tW2,l
L1正则化	∑k∑l|Wk,l|
弹性网络（Elastic Net）	∑k∑tβW2,l+|Wk,l|
最大范数正则化(Max norm regularization)
Drop out

例子：

x = [1,1,1,1]

w1 = [1,0,0,0], w2 = [0.25,0.25,0.25,0.25]

计算他们的损失函数的值都为1，但是加上L2正则化后发现w2的损失比较小。从上可以看到L2正则化是挑选W能均匀展开，也就是能够取到尽可能多的特征的信息。L1能使W中出现很多0，实现特征选择。

softmax分类及corss-entropy loss

softmax分类器，又称为多分类逻辑斯特回归，是二分类中逻辑斯特回归的一般形式。

把分数认为是各个类没有标准化的对数概率，那么作为各个类的概率如下：

P(Y=k|X=xi)=esk∑jesj

最大化对数似然，或者最小化错误的对数似然。

Li=−logP(Y=yi|X=xi)

总结一下： Li=−log(esk∑jesj)

例子：

	score(未经标准化的对数概率)	未经标准化的概率	概率
cat	3.2	24.5	0.13
car	5.1	164.0	0.87
frog	-1.7	0.18	0.00

Li=−log(0.13)=0.89

• 由于e的指数，数据增长太快，所以实际使用的时候可以减去分数的最大值，从而保证计算的稳定。

efyi∑jefj=CefyiC∑jefj=efyi+logC∑jefj+logC

hinge loss & corss-entropy loss

• hinge loss关注那些得分比实际类别得分高，或者接近的点，但是对于那些得分和实际类别低很多的点就不去管了
• corss-entropy loss会对所有的点都进行考量

最优化

设J为损失，那么我们的任务就是找到最优的权重W，能够使得损失J最小。

minJ=L(W;x)

使用梯度下降法来进行这个最优化。每次迭代，把W往负梯度方向调整，就可以减小损失J。

Wi:=Wi−α∂J∂Wi

• 使用mini-batch可以减少计算负担，一般使用2的次方作为batch大小，因为很多向量化运算如果输入是2的次方，运算会更快。
• 使用momentum、Adam等可以优化学习率从而更快得到更好的结果。
• 计算导数有两种方式，数值梯度和微积分，数值梯度是改变一个维度的权重（加上h），然后得到损失结果，用导数的定义来得到导数，代码容易计算太慢，不过可以用这个方法来检查程序是否正确。

参考资料

http://cs231n.github.io/classification/
http://cs231n.github.io/linear-classify/
http://cs231n.github.io/optimization-1/