【NOIP】一篇正式的NOIP2017总结

【注：代码全部放在最后链接】

Day1

T1 小凯的疑惑

【题目描述】

小凯手中有两种面值的金币，两种面值均为正整数且彼此互素。每种金币小凯都有 无数个。在不找零的情况下，仅凭这两种金币，有些物品他是无法准确支付的。现在小 凯想知道在无法准确支付的物品中，最贵的价值是多少金币？注意：输入数据保证存在 小凯无法准确支付的商品。

【输入格式】
输入数据仅一行，包含两个正整数 aa 和 bb，它们之间用一个空格隔开，表示小凯手 中金币的面值。

【输出格式】
输出文件仅一行，一个正整数 NN，表示不找零的情况下，小凯用手中的金币不能准确支付的最贵的物品的价值。

输入样例#1：
3 7
输出样例#1：
11

【输入输出样例 1 说明】

小凯手中有面值为3和7的金币无数个，在不找零的前提下无法准确支付价值为1、 2、4、5、8、11 的物品，其中最贵的物品价值为 11，比 11 贵的物品都能买到，比如：

12=3×4+7×0
13=3×2+7×1
14=3×0+7×2
15=3×5+7×0

【数据范围与约定】
对于 30%的数据： 1≤a,b≤501≤a,b≤50。
对于 60%的数据： 1≤a,b≤1041≤a,b≤104
对于 100%的数据： 1≤a,b≤1091≤a,b≤109

【题目分析】
作为NOIP DAY1T1，个人认为题目不算太好。这样的规律性题目对于水平不高的选手来说是很吃亏的，对于超暴力打表选手反而是赚到了。
考试的时候立刻想到了扩展GCD，然后就推了三张纸，耗时1.5h，直接导致后面没时间做。这样做明显是不理智的，其实在0.5h过后就应该尝试寻找规律，虽然最后推出来了，但对于T2T3的影响显然更大。下一次要转变做题思路。

【解题思路】
在码T2时想到了简单的证明。以下是证明：

首先
gcd(A,B)=1→lcm(A,B)=AB
定义【剩余类】：把所有整数划分成m个等价类，每个等价类由相互同余的整数组成

任何数分成m个剩余类，分别为 mk，mk+1，mk+2，……，mk+(m−1)
分别记为 0(modm)，1(modm)……

而n的倍数肯定分布在这m个剩余类中，并且是平均分配。

设 kmin=min { k|nk∈ { i(modm)) } ,i∈[0,m)
则 nkmin 是 { i(modm) }中n的最小倍数。特别的， nm∈ { 0(modm) }
nkmin 是个标志，它表明{ i(modm) }中 nkmin 后面所有数，即 nkmin+jm 必定都能被组合出来

那也说明最大不能组合数必定小于 nkmin
我们开始寻找 max { nkmin }
lcm(m,n)=mn ，所以很明显 (m−1)n 是最大的
因为 (m−1)n 是 nkmin 中的最大值，所以在剩下的 m−1 个剩余类中，必定有比它小并且能被m和n组合，
这些数就是 (m−1)n−1，(m−1)n−2，……，(m−1)n−(m−1)
所以最大不能被组合数就是 (m−1)n−m

如果m和n不互素，那{1 (mod m)}不能被m组合，同样也不能被n和m组合

不要问我为什么我程序写的式子这么奇怪。

T2 小凯的疑惑

题目描述

小明正在学习一种新的编程语言 A++，刚学会循环语句的他激动地写了好多程序并 给出了他自己算出的时间复杂度，可他的编程老师实在不想一个一个检查小明的程序， 于是你的机会来啦！下面请你编写程序来判断小明对他的每个程序给出的时间复杂度是否正确。

A++语言的循环结构如下：

F i x y
循环体
E

其中F i x y表示新建变量 ii（变量 ii 不可与未被销毁的变量重名）并初始化为 xx， 然后判断 ii 和 yy 的大小关系，若 ii 小于等于 yy 则进入循环，否则不进入。每次循环结束后 ii 都会被修改成 i +1i+1，一旦 ii 大于 yy 终止循环。

xx 和 yy 可以是正整数（xx 和 yy 的大小关系不定）或变量 nn。nn 是一个表示数据规模的变量，在时间复杂度计算中需保留该变量而不能将其视为常数，该数远大于 100。

“E”表示循环体结束。循环体结束时，这个循环体新建的变量也被销毁。

注：本题中为了书写方便，在描述复杂度时，使用大写英文字母“O”表示通常意义下“Θ”的概念。

输入格式：
输入文件第一行一个正整数 tt，表示有 tt（t≤10t≤10） 个程序需要计算时间复杂度。 每个程序我们只需抽取其中 F i x y和E即可计算时间复杂度。注意：循环结构 允许嵌套。

接下来每个程序的第一行包含一个正整数 LL 和一个字符串，LL 代表程序行数，字符 串表示这个程序的复杂度，O(1)表示常数复杂度，O(n^w)表示复杂度为 nw
，其 中w是一个小于100的正整数（输入中不包含引号），输入保证复杂度只有O(1)和O(n^w) 两种类型。

接下来 LL 行代表程序中循环结构中的F i x y或者 E。 程序行若以F开头，表示进入一个循环，之后有空格分离的三个字符（串）i x y， 其中 ii 是一个小写字母（保证不为nn），表示新建的变量名，xx 和 yy 可能是正整数或 nn ，已知若为正整数则一定小于 100。

程序行若以E开头，则表示循环体结束。

输出格式：
输出文件共 tt 行，对应输入的 tt 个程序，每行输出Yes或No或者ERR（输出中不包含引号），若程序实际复杂度与输入给出的复杂度一致则输出Yes，不一致则输出No，若程序有语法错误（其中语法错误只有: ① F 和 E 不匹配 ②新建的变量与已经存在但未被销毁的变量重复两种情况），则输出ERR 。

注意：即使在程序不会执行的循环体中出现了语法错误也会编译错误，要输出 ERR。

【输入样例】
8
2 O(1)
F i 1 1
E
2 O(n^1)
F x 1 n
E
1 O(1)
F x 1 n
4 O(n^2)
F x 5 n
F y 10 n
E
E
4 O(n^2)
F x 9 n
E
F y 2 n
E
4 O(n^1)
F x 9 n
F y n 4
E
E
4 O(1)
F y n 4
F x 9 n
E
E
4 O(n^2)
F x 1 n
F x 1 10
E

【输出样例】
Yes
Yes
ERR
Yes
No
Yes
Yes
ERR

【题目分析】
一道大模拟题目，考试的时候做的还是很快的，只用了15min，debug10min，但是由于我的判断先后顺序错了，挂了一个点，很惊奇。

【解题思路】
按题目模拟即可，注意几个判断的先后顺序。

T3逛公园

【题目描述】

策策同学特别喜欢逛公园。公园可以看成一张N个点M条边构成的有向图，且没有 自环和重边。其中1号点是公园的入口，NN号点是公园的出口，每条边有一个非负权值， 代表策策经过这条边所要花的时间。

策策每天都会去逛公园，他总是从1号点进去，从N号点出来。

策策喜欢新鲜的事物，它不希望有两天逛公园的路线完全一样，同时策策还是一个 特别热爱学习的好孩子，它不希望每天在逛公园这件事上花费太多的时间。如果1号点 到N号点的最短路长为d，那么策策只会喜欢长度不超过d+K的路线。

策策同学想知道总共有多少条满足条件的路线，你能帮帮它吗？

为避免输出过大，答案对P取模。

如果有无穷多条合法的路线，请输出−1。

【输入格式】
第一行包含一个整数 T, 代表数据组数。

接下来T组数据，对于每组数据： 第一行包含四个整数 N,M,K,P，每两个整数之间用一个空格隔开。

接下来M行，每行三个整数 ai,bi,ci ，代表编号为 ai,bi 的点之间有一条权值为 ci 的有向边，每两个整数之间用一个空格隔开。

【输出格式】
输出文件包含T 行，每行一个整数代表答案。

【题目分析】
第一眼看了暴力spfa，30分。
第二眼看了加上k的限制，就是求比最短路长k的路径数，考虑拆点应该是可以的，就是将一条路径拆成三段，1->u，u->v，v->N。然而如果直接拆点跑会跪掉，因为会计算重复。
第三眼想到了可以跑一个DAG上的dp，然后就没有然后了。

处理0环这个东西我居然想了INF这么久，于是我决定先打70分的暴力。
很不错，样例都过了。
思考人生发现用spfa是不是会被卡掉，要换成dijkstra。
于是又是一波操作。
然后处理0环发现是水的，敲，没敲完，暴力跪了——>爆零

总结思路算了（调用UOJ上某犇发的）：

用dijkstra预处理出 dis(1,i),dis(i,N) 。

一条从u到v的长为len的有向边可能出现在答案的路径中，当且仅当 dis(1,u)+len+dis(v,N)<=dis(1,N)+K 。

将每条从u到v的长为len的有向边的长度替换成 len−dis(1,v)+dis(1,u) 后，问题变成了求从1到N的，长度<=K的路径的条数。因为把没用的边删去后，每条边都有可能出现在答案中。

如果此时仍然有仅由长度为0的边构成的环，答案一定是无穷大(判-1)。

然后dp, dp[i][j] 表示从1到j的长度为i的路径的数量。
顺序：先枚举i再枚举j，i的顺序从小到大，j的顺序可以是任意一个由长度为0的边构成的DAG的拓扑序。

时间复杂度 O((N+M)∗(K+logN)) 。

洛谷上是2.7s刚刚好卡过的，如果想在CCF的老爷机上卡过，应该要加一些读入优化什么的。

Day2

T1 奶酪

【题目描述】

现有一块大奶酪，它的高度为 h，它的长度和宽度我们可以认为是无限大的，奶酪 中间有许多 半径相同 的球形空洞。我们可以在这块奶酪中建立空间坐标系，在坐标系中， 奶酪的下表面为 z=0 ，奶酪的上表面为 z=h 。

现在，奶酪的下表面有一只小老鼠 Jerry，它知道奶酪中所有空洞的球心所在的坐 标。如果两个空洞相切或是相交，则 Jerry 可以从其中一个空洞跑到另一个空洞，特别 地，如果一个空洞与下表面相切或是相交，Jerry 则可以从奶酪下表面跑进空洞；如果 一个空洞与上表面相切或是相交，Jerry 则可以从空洞跑到奶酪上表面。

位于奶酪下表面的 Jerry 想知道，在 不破坏奶酪 的情况下，能否利用已有的空洞跑 到奶酪的上表面去?

空间内两点 P1(x1,y1,z1)P2(x2,y2,z2) 的距离公式如下：

dist(P1,P2)=(x1−x2)2+(y1−y2)2+(z1−z2)2−−−−−−−−−−−−−−−−−−−−−−−−−−−−√
​
输入输出格式

输入格式：
每个输入文件包含多组数据。

输入文件的第一行，包含一个正整数 T，代表该输入文件中所含的数据组数。

接下来是 T组数据，每组数据的格式如下： 第一行包含三个正整数 n,h 和 r，两个数之间以一个空格分开，分别代表奶酪中空 洞的数量，奶酪的高度和空洞的半径。

接下来的 n 行，每行包含三个整数 x,y,z，两个数之间以一个空格分开，表示空 洞球心坐标为 (x,y,z) 。

输出格式：
输出文件包含 T 行，分别对应 T 组数据的答案，如果在第 i 组数据中，Jerry 能从下 表面跑到上表面，则输出Yes，如果不能，则输出No （均不包含引号）。

【题目分析】
看一眼题目后，发现是一道关于几何的题目，有点慌。
再看一眼数据，1000，n^2暴力过。
场上没有思考什么，直接开LL，用sqrt什么的乱搞，然后bfs一遍。
出来以后说实话很慌，然而最后还是A掉的。

【解题思路】
暴力枚举两个点是否联通，连边后bfs

T2 宝藏

【题目描述】

参与考古挖掘的小明得到了一份藏宝图，藏宝图上标出了 n 个深埋在地下的宝藏屋， 也给出了这 n 个宝藏屋之间可供开发的 m 条道路和它们的长度。

小明决心亲自前往挖掘所有宝藏屋中的宝藏。但是，每个宝藏屋距离地面都很远， 也就是说，从地面打通一条到某个宝藏屋的道路是很困难的，而开发宝藏屋之间的道路 则相对容易很多。

小明的决心感动了考古挖掘的赞助商，赞助商决定免费赞助他打通一条从地面到某 个宝藏屋的通道，通往哪个宝藏屋则由小明来决定。

在此基础上，小明还需要考虑如何开凿宝藏屋之间的道路。已经开凿出的道路可以 任意通行不消耗代价。每开凿出一条新道路，小明就会与考古队一起挖掘出由该条道路 所能到达的宝藏屋的宝藏。另外，小明不想开发无用道路，即两个已经被挖掘过的宝藏 屋之间的道路无需再开发。

新开发一条道路的代价是： L×K

L代表这条道路的长度，K代表从赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的 宝藏屋的数量（包括赞助商帮你打通的宝藏屋和这条道路起点的宝藏屋） 。

请你编写程序为小明选定由赞助商打通的宝藏屋和之后开凿的道路，使得工程总代 价最小，并输出这个最小值。

【输入格式】
第一行两个用空格分离的正整数 n 和 m，代表宝藏屋的个数和道路数。

接下来 m 行，每行三个用空格分离的正整数，分别是由一条道路连接的两个宝藏 屋的编号（编号为 1~n），和这条道路的长度 v。

【输出格式】
输出共一行，一个正整数，表示最小的总代价。

输入样例#1：
4 5
1 2 1
1 3 3
1 4 1
2 3 4
3 4 1
输出样例#1：
4

输入样例#2：
4 5
1 2 1
1 3 3
1 4 1
2 3 4
3 4 2
输出样例#2：
5

【样例解释1】

小明选定让赞助商打通了 1 号宝藏屋。小明开发了道路 1→2 ，挖掘了 2 号宝 藏。开发了道路 1→4 ，挖掘了 4 号宝藏。还开发了道路 4→3 ，挖掘了 3 号宝 藏。工程总代价为： 1×1+1×1+1×2=4
【样例解释2】

小明选定让赞助商打通了 1 号宝藏屋。小明开发了道路 1→2 ，挖掘了 2 号宝 藏。开发了道路 1→3 ，挖掘了 3 号宝藏。还开发了道路 1→4 ，挖掘了 4 号宝 藏。工程总代价为： 1×1+3×1+1×1=5
【数据规模与约定】
对于 20%的数据： 保证输入是一棵树， 1≤n≤8，v≤5000 且所有的 v 都相等。

对于 40%的数据： 1≤n≤8，0≤m≤1000，v≤5000 且所有的 v 都相等。

对于 70%的数据： 1≤n≤8，0≤m≤1000，v≤5000

对于 100%的数据： 1≤n≤12，0≤m≤1000，v≤500000

【题目分析】
数据一眼看出来状压dp，然而个人对状压的理解实在是弱，于是打了一个爆搜，预计70居然只有15。

【解题思路】
直接用 fs ​表示状态是s的时候最小值，发现可能从不正确的地方打向下的洞，那怎么办？？

那么我们就枚举一个根节点，就是用 fis 表示以i为根状态是s的时候最小值，
用一个 deepisj 表示以i为根状态是s的时候，当前做到j的节点深度。

然后就直接 O(n2) 更新就行了。

以上是根据柯神的解释然后个人乱搞的，可以看出理解很浅，下面看看别人的说法= =

==================分割线=================

设 f[dep][S] 为到第dep层目前用了S状态的点的总方案数目

考虑在它的补集里面枚举下一层的点数，然后直接转移就行了。

f[i+1][s1|s2]=min(f[i+1][s1|s2],f[i][s1]+val[s2][s1]); 其中 val[s2][s1] 表示s2的每个点到s1所需要的最小总花费。

如果直接做的话是 O(3n×n3) 的

发现val这个东西对于每一个s1s2是一样的，那么预处理一下

先预处理点到集合的，再处理集合到集合的。

总复杂度 O(3n×n)

T3 列队

【题目描述】

Sylvia 是一个热爱学习的女♂孩子。

前段时间，Sylvia 参加了学校的军训。众所周知，军训的时候需要站方阵。

Sylvia 所在的方阵中有 n×m 名学生，方阵的行数为 n，列数为 m。

为了便于管理，教官在训练开始时，按照从前到后，从左到右的顺序给方阵中 的学生从 1 到 n×m 编上了号码（参见后面的样例）。即：初始时，第 i 行第 jj列 的学生的编号是 (i−1)×m+j 。

然而在练习方阵的时候，经常会有学生因为各种各样的事情需要离队。在一天 中，一共发生了 q件这样的离队事件。每一次离队事件可以用数对 (x,y)(1≤x≤n,1≤y≤m) 描述，表示第 x 行第 y 列的学生离队。

在有学生离队后，队伍中出现了一个空位。为了队伍的整齐，教官会依次下达 这样的两条指令：

向左看齐。这时第一列保持不动，所有学生向左填补空缺。不难发现在这条 指令之后，空位在第 x 行第 m 列。

向前看齐。这时第一行保持不动，所有学生向前填补空缺。不难发现在这条 指令之后，空位在第 n 行第 m 列。
教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后， 下一个学生才能离队。因此在每一个离队的学生要归队时，队伍中有且仅有第 n 行 第 m 列一个空位，这时这个学生会自然地填补到这个位置。

因为站方阵真的很无聊，所以 Sylvia 想要计算每一次离队事件中，离队的同学 的编号是多少。

注意：每一个同学的编号不会随着离队事件的发生而改变，在发生离队事件后 方阵中同学的编号可能是乱序的。

输入输出格式

输入格式：
输入共 q+1 行。

第 1 行包含 3 个用空格分隔的正整数 n, m, q，表示方阵大小是 n 行 m列，一共发 生了 q 次事件。

接下来 q 行按照事件发生顺序描述了 q 件事件。每一行是两个整数 x, y,用一个空 格分隔，表示这个离队事件中离队的学生当时排在第 x 行第 y 列。

输出格式：
按照事件输入的顺序，每一个事件输出一行一个整数，表示这个离队事件中离队学 生的编号。

输入样例#1：
2 2 3
1 1
2 2
1 2
输出样例#1：
1
1
4
【数据范围】

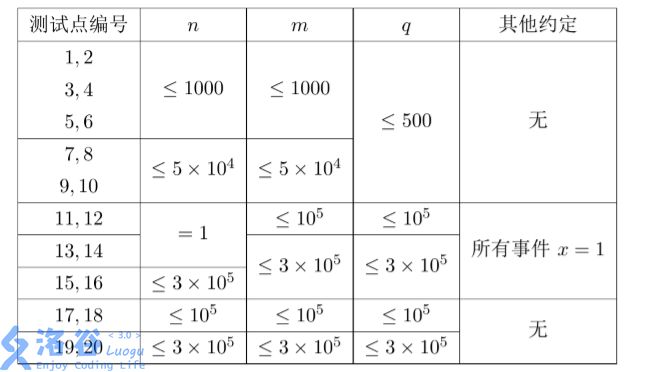
【题目分析】
这道题显然是一道数据结构题。
考试的时候是想到50+30的暴力，然后后30的线段树写挂了。

【解题思路】
考虑前50pt，因为我们发现n和m是 5×104 ，然后q只有500。那么我们可以离线做，只存储这50行+1列的信息，暴力模拟即可。
考虑 x=1 时的情况，发现可以展开成一条链，用线段树维护即可。

然后想100pt

首先我们把最后一列单独考虑。
我们观察每个操作，可以分解成在当前行中间删除一个元素，然后在末尾插入一个元素。然后在最后一列中间删除一个元素，在末尾插入一个元素。

发现这个东西就是一个Splay，乱搞一下就可以，时间复杂度 O(nlogn) 。

然而我不会Splay怎么办？

发现每一行是独立的，我们可以开n个线段树来存储。

那么问题可以转换为两种操作：
First：找到第 k 大的数并把它删掉。
Second：加一个数在序列后面。

注意到加入只是加入到 序列的末尾，且加入数 ≤3×105 ，

所以可以用预留 3×105 位置直接维护，查询在线段树上进行二叉查找就行啦。

然后就是要动态开节点，因为内存不够哇。

总的时间复杂度 O(nlogn) 。

============以下是DYH神神神犇犇犇的思路===========

我们考虑怎么精妙地实现这个过程，首先我们把最后一列单独的看成一个对象，每个行看成一个对象。对于每个单独的对象，要执行的过程都是中间删除一个元素，末尾插入一个元素。要在线实现这个过程是很困难的。

我们先考虑怎么离线做这个事情。离线做最大的问题是你不知道末尾插入的元素是什么。不过我们可以建立一个虚拟的元素，表示这个元素是某次操2作出来的答案。最后所有的操作都结束之后，再看一下这些虚拟的元素对应的什么，然后输出即可。

所以问题转化为了单个对象的操作，假设有 Q 个操作，我们希望能在 O(Q log n) 的时间复杂度内处理这些操作，并且每个对象初始化是一个 1 到 n − 1 的列表 (对最后一列是 1 到 n)。

为了避免使用平衡树，我们将这个考虑成一个静态的数组 A 存储每个位置的元素，并且用一个数组 B，其中每个数都是 0/1 表示有没有这个元素是否还未被删除。

这个时候在末尾插入元素的操作就只要把这个静态数组末尾复制，然后把 B 数组对应的位置改成 1。

而删除操作需要首先算出前缀和为 k 的位置，然后把 B 这个位置改成 0。

这些操作都可以使用树状数组解决，因为树状数组本来就有个树的结构，所以可以直接在树状数组上二分并且统计，时间复杂度是 O(log n) 的。

现在问题还有初始化，我们需要一个 1 到 n − 1 的数组 A 和全是 1 的数组 B。

有两种解决方法，一种是每个对象做完之后把树状数组上的修改全部撤销。一种是把一开始初始化的树状数组备份，并且给每个位置记一个时间戳。每次访问一个位置的时候我们先看时间戳，如果不对的话，也就是在这个对象处理的时候这个位置没有初始化过，就先把这个位置的值从一开始的备份里拷贝过来，然后更新时间戳。

然后就这样吧。

最后是代码链接：
Day1的神奇代码
Day2的神奇代码