机器学习实战笔记——k-means算法

一、算法原理

    k-均值算法是一种无监督学习算法。在输入数据集中不包括标签，通过k-均值算法为每个样本添加标签，相同标签样本具有共同特征。

    对于数据集D={x1，x2，...，xm}，划分为k个簇C1，C2，...，Ck。对象与该簇的距离用dist(p，Ci)表示，其中dist(x，y)是两点x和y之间的欧式距离。最小化平方差

也就是对于每个簇中的每个对象，求对象到簇中心距离的平方，然后求和。E越小说明簇越紧凑，聚类效果越好。

k-均值算法流程如下：

（1）先在D中随机选取k个对象，作为k个簇的初始值；

（2）对剩下的每个对象，按照欧氏距离最小原则，将它分配到最相似的一个簇（用距离刻画）；

（3）重新计算每个簇的均值作为新的聚类中心

（4）重复（2）（3）步骤，直到中心值不再变化或者变化很小时，聚类完成。

输入:
  k:簇的数目
  D:包含n个对象的数据集
输出:k个簇的集合
方法:
（1）从D中任意选择k个对象作为初始簇中心；
（2）repeat
（3）  根据簇中对象的均值，将每个对>象分配到最相似的簇；
（4）  更新簇均值，即重新计算每个簇中对象的均值；
（5）util不在发生变化；

2、代码部分

import numpy as np

def loadDataSet(fileName):      #general function to parse tab -delimited floats
    dataMat = []                #assume last column is target value
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        #fltLine = map(float,curLine) 是Python2的用法
        #python3
        fltLine = list(map(float,curLine)) #map all elements to float()
        dataMat.append(fltLine)
    return dataMat

def distEclud(vecA, vecB):
    return sqrt(sum(power(vecA - vecB, 2))) #la.norm(vecA-vecB)

def randCent(dataSet, k):
    n = shape(dataSet)[1]
    centroids = mat(zeros((k,n)))#create centroid mat
    for j in range(n):#create random cluster centers, within bounds of each dimension
        minJ = min(dataSet[:,j]) 
        rangeJ = float(max(dataSet[:,j]) - minJ)
        centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1))
    return centroids
    
def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
    m = shape(dataSet)[0]
    clusterAssment = mat(zeros((m,2)))#create mat to assign data points 
                                      #to a centroid, also holds SE of each point
    centroids = createCent(dataSet, k)
    clusterChanged = True
    while clusterChanged:
        clusterChanged = False
        for i in range(m):#for each data point assign it to the closest centroid
            minDist = inf; minIndex = -1
            for j in range(k):
                distJI = distMeas(centroids[j,:],dataSet[i,:])
                if distJI < minDist:
                    minDist = distJI; minIndex = j
            if clusterAssment[i,0] != minIndex: clusterChanged = True
            clusterAssment[i,:] = minIndex,minDist**2
        print (centroids)
        for cent in range(k):#recalculate centroids
            ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]#get all the point in this cluster
            centroids[cent,:] = mean(ptsInClust, axis=0) #assign centroid to mean 
    return centroids, clusterAssment


import matplotlib.pyplot as plt
def draw(dataMat,centroids,clusterAssment):
    k=len(centroids)
    fig = plt.figure()  
    ax = fig.add_subplot(111)  
    ax.scatter(centroids[:,0].tolist(),centroids[:,1].tolist(),marker='+',c='r')  
    markers=['o','s','v','*'];colors=['blue','green','yellow','red']  
    for i in range(k):  
        data_class=dataMat[nonzero(clusterAssment[:,0].A == i)[0]]  
        ax.scatter(data_class[:,0].tolist(),data_class[:,1].tolist(),marker=markers[i],c=colors[i])  
    plt.show()
    
if __name__ =="__main__":  
    dataMat = mat(loadDataSet('testSet2.txt'))  
    print("簇质心：\n",randCent(dataMat,2))  
    print("距离：\n",distEclud(dataMat[0],dataMat[1]))   
    myCentroids, clustAssing = kMeans(dataMat,3)  
    print("类质心：\n",myCentroids)  
    print("点分配结果：\n",clustAssing)  
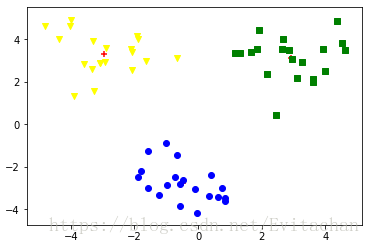
    draw(dataMat,myCentroids, clustAssing)  

当k=3时，聚类结果如图

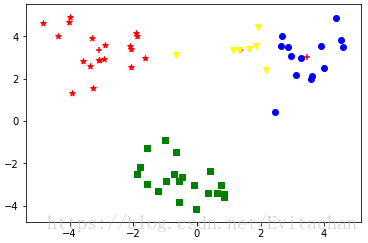
k=4时，聚类结果如图

肉眼观察的话，以三个聚类中心效果最好。

3、二分k-均值算法

    在k-均值算法中，簇的数目k是用户预先定义的变量，在不知道k值是否合适的情况下，聚类结果很可能是局部最优解而不是全局最优解。为了提高聚类指标，我们定义一个新的指标：SSE（Sum of Squared Error，误差平方和）。SSE越小表示数据越接近聚类中心，聚类效果越好。

二分k-均值算法流程为：

（1）将所有点看成一个簇，按照k-means算法分成两个簇

（2）选择可以进行划分的簇，依据是划分后使得SSE最小

（3）将可划分的簇按照k-means算法划分为两个簇

（4）重复（2）（3）步骤直到簇的数目为k

def biKmeans(dataSet, k, distMeas=distEclud):
    m = shape(dataSet)[0]
    clusterAssment = mat(zeros((m,2)))
    centroid0 = mean(dataSet, axis=0).tolist()[0]
    centList =[centroid0] #create a list with one centroid
    for j in range(m):#calc initial Error
        clusterAssment[j,1] = distMeas(mat(centroid0), dataSet[j,:])**2
    while (len(centList) < k):
        lowestSSE = inf
        for i in range(len(centList)):
            ptsInCurrCluster = dataSet[nonzero(clusterAssment[:,0].A==i)[0],:]#get the data points currently in cluster i
            centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas)
            sseSplit = sum(splitClustAss[:,1])#compare the SSE to the currrent minimum
            sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1])
            print ("sseSplit, and notSplit: ",sseSplit,sseNotSplit)
            if (sseSplit + sseNotSplit) < lowestSSE:
                bestCentToSplit = i
                bestNewCents = centroidMat
                bestClustAss = splitClustAss.copy()
                lowestSSE = sseSplit + sseNotSplit
        bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList) #change 1 to 3,4, or whatever
        bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit
        print ('the bestCentToSplit is: ',bestCentToSplit)
        print ('the len of bestClustAss is: ', len(bestClustAss))
        centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0]#replace a centroid with two best centroids 
        centList.append(bestNewCents[1,:].tolist()[0])
        clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss#reassign new clusters, and SSE
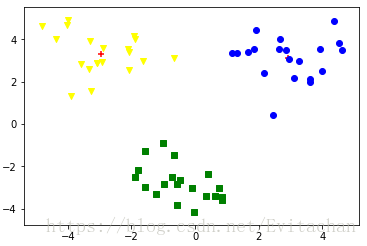
    return mat(centList), clusterAssment

k=3时

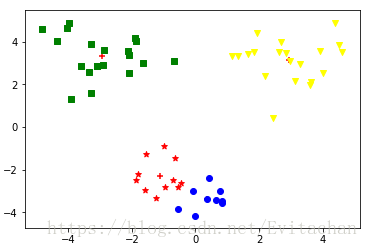
k=4时

k=3时，两种算法结果一样。k=4时，二分k-means算法聚类结果更好。

4、总结

1. k-means算法对初始值敏感，由于每次初始值选择是随机的，聚类结果可能不同。

2. k-means算法对噪声和离群点敏感，为了降低对噪声和离群点的敏感性，可以不采用簇中对象的均值作为参照点，而是挑选实际对象来代表簇，每个簇使用一个代表对象（k-中心点算法）。

3. 二分k-means算法是k-means算法的改进算法，相较而言，二分k-means算法效率更高，因为减少了相似度计算。

参考资料：

【1】《机器学习实战》 Peter Harrington 著  人民邮电出版社

【2】《机器学习》 周志华 著  清华大学出版社

【3】《数据挖掘概念与技术》 Jiawei Han等 著  机械工业出版社