最小生成树-Prim算法
生成树
生成树是连通图的最小连通子图。所谓最小是指:若在树中任意增加一条边,则将出现一个回路;若去掉一条边,将会使之变成非连通图。按照该定义,n个顶点的连通网络的生成树有n个顶点,n-1条边。
可知用不同的遍历图的方法,可以得到不同的生成树;从不同的顶点出发,也可能得到不同的生成树。
最小生成树
生成树各边的权值总和称为生成树的权,权最小的生成树称为最小生成树。
最小生成树的概念可以应用到许多实际问题中。例如:以尽可能低的总造价建设城市间的通讯网络,以把10个城市联系在一起。在这10个城市中,任意两个城市间都可以建造通讯线路,通讯线路的造价依据城市间的距离不同而有不同的造价,可以构造一个通讯线路造价网络,在网络中,每个顶点表示城市,顶点之间的边表示城市之间可构造通讯线路,每条边的权值表示该条通讯线路的造价,要想使总的造价最低,实际上就是寻找该网络的最小生成树。
常见的构造最小生成树的方法有Prim算法和Kruskal算法。
下面介绍Prim算法
Prim算法
Prim算法通常以邻接矩阵作为储存结构。
它的基本思想是以顶点为主导地位,从起始顶点出发,通过选择当前可用的最小权值边把顶点加入到生成树当中来:
1.从连通网络N={V,E}中的某一顶点U0出发,选择与它关联的具有最小权值的边(U0,V),将其顶点加入到生成树的顶点集合U中。
2.以后每一步从一个顶点在U中,而另一个顶点不在U中的各条边中选择权值最小的边(U,V),把它的顶点加入到集合U中。如此继续下去,直到网络中的所有顶点都加入到生成树顶点集合U中为止。
可行性证明:
设prim生成的树为G0
假设存在Gmin使得cost(Gmin)
则在Gmin中存在(u,v)不属于G0
将(u,v)加入G0中可得一个环,且(u,v)不是该环的最长边
这与prim每次生成最短边矛盾
故假设不成立,得证.
下面看具体数据和模拟过程
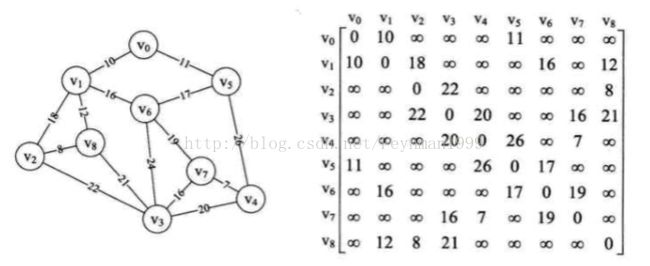
现在有一个存储结构为邻接矩阵的G,有9个顶点,它的arc二维数组如上图所示。
于是Prim算法的代码如下,其中INFINITY为权值极大值,不妨设为0xfffffff,MAXVEX为顶点个数最大值,此处大于等于9即可。
void MinSpanTree_Prim(MGraph G)
{
int min,i,j,k;
int adjvex[MAXVEX];//保存相关顶点下标以记录路径
int lowcost[MAXVEX];//保存相关顶点间边的权值
lowcost[0]=0;//初始化第一个权值为0,即v0加入生成树
//lowcost的值为0,在这里就是此下标的顶点已经加入生成树
adjvex[0]=0;//初始化到第一个顶点的下标路径为0
for(i=1;i1.程序开始运行,我们由第4~5行,创建了两个一维数组lowcost和adjvex,长度都为顶点个数9。他们的作用后面会体现。
2.第6~8行分别给这两个数组的第一个下标位赋值为0,adjvex[0]=0意思就是现在从顶点V0开始(事实上,最小生成树从哪个顶点开始计算都无所谓,我们假定从V0开始),lowcost[0]=0就表示V0已经被纳入到最小生成树中,之后凡是lowcost数组中的值被设置为0就是表示此下标的顶点被纳入最小生成树。
3.第9~12行表示我们读取邻接矩阵的第一行数据。将数值赋值给lowcost数组,所以此时lowcost数组值为{0,10,inf,inf,inf,11,inf,inf,inf},而adjvex则全部为0。此时,已经完成了整个初始化的工作,准备开始生成。
4.第13~35行,整个循环过程就是构造最小生成树的过程。
5.第14~16行,将min设置为了一个极大值0x3fffffff,它的目的是为了之后找到一定范围内的最小权值。j是用来做顶点下标循环的变量,k是用来存储最小权值的顶点下标。
6. 第17~24行,循环中不断修改min为当前lowcost数组中最小值,并用k保留此最小值的顶点下标。经过循环后,min=10,k=1。第19行if判断的lowcost[j]!=0表示已经是生成树的顶点不参与最小权值的查找。
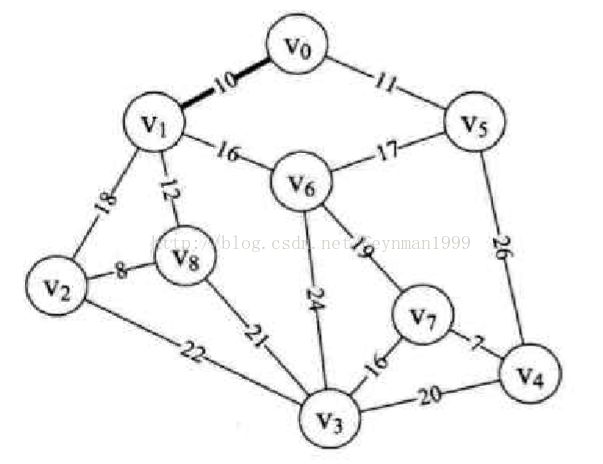
7.第25行,因k=1,adjvex[1]=0,所以打印结果为(0,1),表示V0至V1边为最小生成树的第一条边。如下图所示:
8.第26行,此时因k=1,我们将lowcost[k]=0就是说顶点v1纳入到最小生成树中。此时lowcost数组值为{0,0,inf,inf,inf,11,inf,inf,inf}。
9.第27~33行,j循环由1至8,因k=1,查找邻接矩阵的第v1行的各个权值,与lowcost的对应值比较,若更小则修改lowcost值,并将k值存入adjvex数组中。因第v1行有18、16、12均比0x3fffffff小,所以最终lowcost数组的值为:{0,0,18,inf,inf,11,16,inf,12}。adjvex数组的值为:{0,0,1,0,0,0,1,0,1}。这里第30行if判断的lowcost[j]!=0也说明v0和v1已经是生成树的顶点不参与最小权值的对比了。
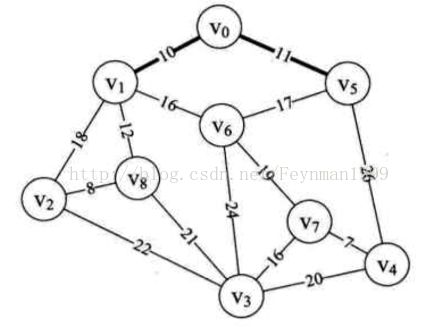
10.再次循环,由第14行到25行,此时min=11,k=5,adjvex[5]=0。因此打印结构为(0,5)。表示v0至v5边为最小生成树的第二条边,如下图所示:
11.接下来执行到33行,lowcost数组的值为:{0,0,18,inf,26,0,16,inf,12}。adjvex数组的值为:{0,0,1,0,5,0,1,0,1}。
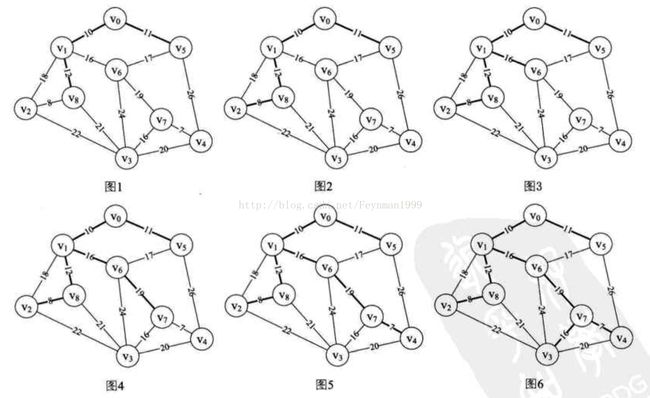
12.之后经过类似的模拟,如下图:
总结
使用邻接矩阵作为存储结构的Prim算法的时间复杂度为O(V2),如果使用二叉堆与邻接表表示的话,Prim算法的时间复杂度可缩减为O(E log V),其中E为连通图的边数,V为顶点数。
如果使用较复杂的斐波那契堆,则可将运行时间进一步缩短为O(E + V log V),这在连通图足够密集时(边较多,即E满足Ω(V log V))可较显著地提高运行速度。
例:POJ - 2395
求minispan_tree中longest edge
//求minispan_tree中longest edge
//O(N^2)
//vector中存每个点所连边的序号 通过边集数组索引
#include
#include
#include
using namespace std;
struct Edge{
int from,to,dist;
Edge(int u,int v,int w):from(u),to(v),dist(w){}
};
const int maxn=10010;
const int inf=0x3f3f3f3f;
int ans;
vector edges;
vector G[maxn];
int n,m;
void addEdge(int u,int v,int w){
edges.push_back(Edge(u,v,w));
edges.push_back(Edge(v,u,w));
int size=edges.size();
G[u].push_back(size-2);
G[v].push_back(size-1);
}
int adjvex[maxn];//最小生成树上每个点的前驱
int lowcost[maxn];//前驱到这个点的距离,即目前最小生成树中到该点的最短距离
bool v[maxn];//是否在生成树中的标记
void Prim()
{
for(int i=1;i<=n;++i) lowcost[i]=inf;
lowcost[1]=0;
for(int i=1;i<=n;++i) adjvex[i]=0,v[i]=0;
adjvex[1]=1;
for(int i=1;i<=n;++i){
//for(int i=1;i<=n;++i) cout<
//求minispan_tree中longest edge
//O(N^2)
//vector中直接存每个边的信息(常用pair)first表示所连点的编号 second表示距离
#include
#include
#include
using namespace std;
#define mp make_pair
const int maxn=10010;
const int inf=0x3f3f3f3f;
int ans;
vector > G[maxn];
int n,m;
void addEdge(int u,int v,int w){
G[u].push_back(mp(v,w));
G[v].push_back(mp(u,w));
}
int adjvex[maxn];//最小生成树上每个点的前驱
int lowcost[maxn];//前驱到这个点的距离
int v[maxn];//是否在生成树中的标记
void Prim()
{
for(int i=1;i<=n;++i) lowcost[i]=inf;
lowcost[1]=0;
for(int i=1;i<=n;++i) adjvex[i]=0,v[i]=0;
adjvex[1]=1;
for(int i=1;i<=n;++i){
//for(int i=1;i<=n;++i) cout<