python 曲线拟合(numpy.polyfit、scipy.optimize.curve_fit)
小白的学习笔记,欢迎各位大神批评指正。
python 曲线拟合
(一次二次比较简单,直接使用numpy中的函数即可,来自 <https://blog.csdn.net/yefengzhichen/article/details/52767733> )
1.多项式拟合
(1)简介
z= numpy.polyfit(x, y, deg, rcond=None, full=False, w=None, cov=False)[source]
Deg Degree of the fitting polynomial 1次多项式即为线性,deg次数太高会有震荡
采用最小二乘多项式拟合,返回多项式的系数
p = np.poly1d(z) 可以获得多项式(一元多次函数) 或者直接用yvals=np.polyval(z,5)
x = p(5) x带入多项式求得一个值
(2)官方文档
numpy.polyfit
来自
The Polynomial.fit class method is recommended for new code as it is more stable numerically. See the documentation of the method for more information.
numpy.poly1d
来自
numpy.polyval
来自
(3)例子 来自
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(1,17,1)
y = np.array([4.00,6.40,8.00,8.80,9.22,9.50,9.70,9.86,10.00,10.20,10.32,10.42,10.50,10.55,10.58,10.60])
z1 = np.polyfit(x,y,3) #用3次多项式拟合 可以改为5 次多项式。。。。 返回三次多项式系数
p1= np.poly1d(z1)
print(p1) #在屏幕上打印拟合多项式
yvals = p1(x)#也可以使用yvals=np.polyval(z1,x)
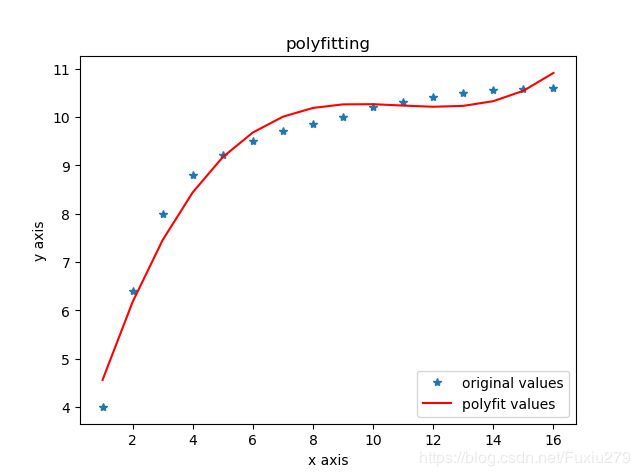
plot1 = plt.plot(x,y,'*',label='original values')
plot2 = plt.plot(x,yvals,'r',label='polyfit values')
plt.xlabel('xaxis')
plt.ylabel('yaxis')
plt.legend(loc=4) #指定legend的位置,读者可以自己help它的用法
plt.title('polyfitting')
plt.show()
plt.savefig('p1.png')
2.scipy.optimize.curve_fit
(1)简介
Fitting data with SciPy 来自
The scipy.optimize module contains a least squares curve fit routine that requires as input a user-defined fitting function (in our case fitFunc ), the x-axis data (in our case, t) and the y-axis data (in our case, noisy). The curve_fit routine returns an array of fit parameters, and a matrix of covariance data 协方差(the square root of the diagonal values 对角线值are the 1-sigma uncertainties on the fit parameters—provided you have a reasonable fit in the first place.):
当然,curve_fit()函数不仅可以用于直线、二次曲线、三次曲线的拟合和绘制,仿照代码中的形式,可以适用于任意形式的曲线的拟合和绘制,只要定义好合适的曲线方程即可。来自
调用curve_fit()函数,核心步骤:
1) 定义需要拟合的函数类型,如:
def func(x, a, b):
return a*np.exp(b/x)
2) 调用 popt, pcov = curve_fit(func, x, y) 函数进行拟合,并将拟合系数存储在popt中,a=popt[0]、b=popt[1]进行调用;
3) 调用func(x, a, b)函数,其中x表示横轴表,a、b表示对应的参数。
来自
(2)官方文档
scipy.optimize.curve_fit 来自
(3)例子 来自
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import numpy as np
#用指数形式来拟合
x=np.arange(1,17,1)
y=np.array([4.00,6.40,8.00,8.80,9.22,9.50,9.70,9.86,10.00,10.20,10.32,10.42,10.50,10.55,10.58,10.60])
def func(x,a,b):
return a*np.exp(b/x)
popt,pcov=curve_fit(func,x,y)
a=popt[0] #popt里面是拟合系数,读者可以自己help其用法
b=popt[1]
yvals=func(x,a,b)
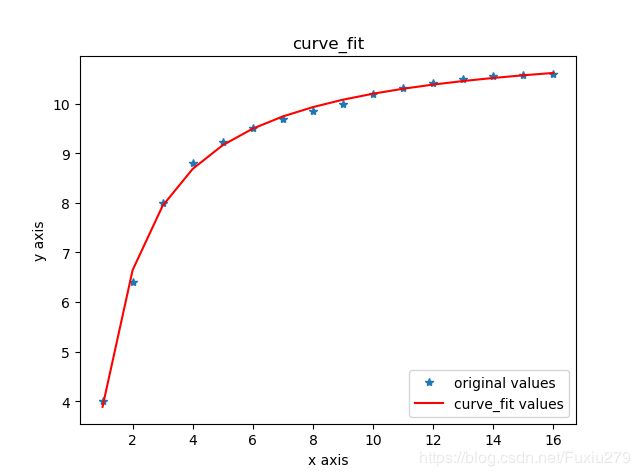
plot1=plt.plot(x,y,'*',label='original values')
plot2=plt.plot(x,yvals,'r',label='curve_fit values')
plt.xlabel('xaxis')
plt.ylabel('yaxis')
plt.legend(loc=4) #指定legend的位置,读者可以自己help它的用法
plt.title('curve_fit')
plt.show()
plt.savefig('p2.png')
1.幂函数和指数函数的例子
python指数、幂数拟合curve_fit 来自
2.高斯拟合的例子
python scipy.optimize curve_fit 多高斯拟合 来自
def f_gauss(x, A, B, C, sigma):
return A*np.exp(-(x-B)**2/(2*sigma**2)) + C
来自
其他:
可以借助Pandas导入数据,再进行处理
来自
矩阵运算:
Python 二维曲线拟合
来自
python_numpy最小二乘法的直线、曲线拟合
来自
3.使用神经网络拟合曲线(MATLAB/Python)
来自