神经网络中的BP算法(原理和推导)
BP算法介绍
BP算法(Background Propagation Alogorithm), 即误差逆传播算法,是训练多层前馈神经网络的一种最经典的算法,通过BP算法可以学得网络的权重和阈值,且具有可靠的收敛性。
网络结构
首先对所用的符号和变量做约定,这里采用《机器学习》中的命名
训练集: D={(x1,y1),(x2,y2),...,(xm,ym)},xi∈Rd,yi∈Rl
即输入的x有d个属性,输出y有l个属性,均以向量表示
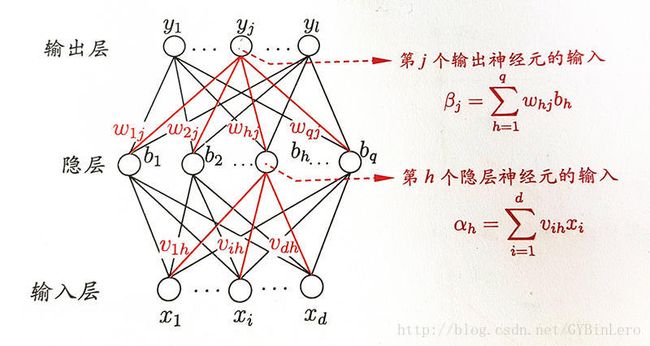
输入层到隐层的权重以 υih 表示,隐层到输出层的权重以 ωhj 表示
隐层神经元输入和输出层神经元输入如图所示
基本思想
通过前向传播确定误差,再利用反向传播减少误差
优化基于梯度下降法(gradient decenet)进行,对参数的更新方式为(其中 η 为学习率)
ω=ω−η∂Ek∂ωhj
- 将输入确定为常量1,网络的阈值学习可以等效为权重的学习,本文仅作权重的讨论
前向传播过程:
将输入值传入神经网络,逐层将信号前传,计算输出层的结果 yˆ
计算输出值 yˆ和 yj 的误差,通常采用均方误差(mse)
Ek=12Σlj=1(yˆkj−ykj)2
反向传播过程:
输入层神经元
根据优化策略,减小输出误差需要计算误差关于其输入权的梯度,即 ∂Ek∂ωhj
利用求导的链式法则(Chain Rule),可以将其展开为
∂Ek∂ωhj = ∂Ek∂yˆkj⋅∂yˆkj∂βj⋅∂βj∂ωhj
这个表达式初看上去有点复杂,我们可以一步一步来计算它。
第一项 ∂Ek∂yˆkj
这一项是误差对输出求偏导,由上文提到的均方误差公式可以直接求导计算,结果为 −(yˆkj−ykj)
第二项 ∂yˆkj∂βj
这一项是输出对输入求偏导,即对输出层的激励函数求偏导,在这里选用sigmoid函数作为激励函数
sigmoid函数: 11+e−z 具有非常优秀的性质,其中包括导数可用自身表示, f′(x)=f(x)(1−f(x))
因此,该项导数可直接写出,为 =yˆkj(1−yˆ)
第三项 ∂βj∂ωhj
这一项是输入对权重求偏导,由图中 βj 的定义直接计算,结果为 bh
综上,输出层神经元的误差为
δωhj=−(yˆkj−ykj)yˆkj(1−yˆ)bh
隐层神经元
对于隐层神经元,输入权梯度为
∂Ek∂bh⋅∂bh∂αh
同样地,激活函数也为sigmoid,可以快速写出第二项导数
第一项继续运用链式法则,先求误差对输入的偏导 ∂Ek∂βj ,再求输入对隐层神经元的偏导 ∂βj∂bh ,方法同上
需要注意的是,隐层神经元不能直接确定对误差的影响,因此对所有输出神经元都需要考虑输入
(在输出层时只考虑一个待求神经元的输入)
最终求得的导数
δωih=−(yˆkj−ykj)yˆkj(1−yˆ)Σlj=1ωhjbh(1−bh)xi
BP算法遇到的问题
BP算法的精髓在于逐层反向更新权重,基于梯度下降的学习使它具有可靠的学习能力,但也同时会被梯度下降算法固有的缺陷所影响,包括
- 在累积误差下降到一定程度后可能出现梯度消失现象
- 可能收敛至局部最优解
- 过于复杂的网络结构可能导致训练结果过拟合
问题1和2涉及到梯度下降法的优化问题,解决的方法有
- 多次设定参数初始值和学习率
- 使用不同的优化版梯度下降算法(SGD,ADAM等)
- 运用模拟退火技术
问题3解决方法有
- 人工早停,弱测试集误差增高则停止训练
- 对网络复杂度增加正则项