Python多元线性回归-sklearn.linear_model,并对其预测结果评估
python 实现案例
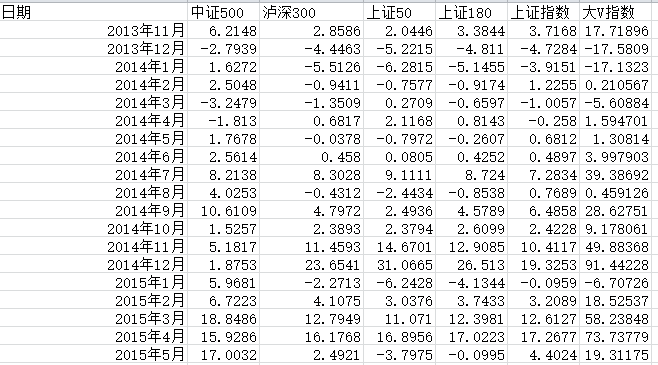
1、选取数据
#!usr/bin/env python
#_*_ coding:utf-8 _*_
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib as mpl #显示中文
def mul_lr():
pd_data=pd.read_excel('C:\\Users\\lenovo\\Desktop\\test.xlsx')
print('pd_data.head(10)=\n{}'.format(pd_data.head(10)))
mpl.rcParams['font.sans-serif'] = ['SimHei'] #配置显示中文,否则乱码
mpl.rcParams['axes.unicode_minus']=False #用来正常显示负号,如果是plt画图,则将mlp换成plt
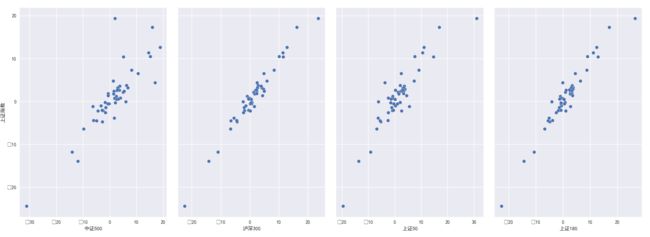
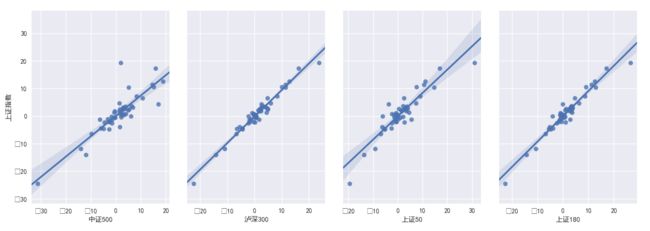
sns.pairplot(pd_data, x_vars=['中证500','泸深300','上证50','上证180'], y_vars='上证指数',kind="reg", size=5, aspect=0.7)
plt.show()#注意必须加上这一句,否则无法显示。添加参数kind=”reg”结果,关于画图方面可[参考连接]
#####2、构建训练集与测试级,并构建模型
from sklearn.model_selection import train_test_split #这里是引用了交叉验证
from sklearn.linear_model import LinearRegression #线性回归
from sklearn import metrics
import numpy as np
import matplotlib.pyplot as plt
def mul_lr(): #续前面代码
#剔除日期数据,一般没有这列可不执行,选取以下数据http://blog.csdn.net/chixujohnny/article/details/51095817
X=pd_data.loc[:,('中证500','泸深300','上证50','上证180')]
y=pd_data.loc[:,'上证指数']
X_train,X_test, y_train, y_test = train_test_split(X,y,test_size = 0.2,random_state=100)
print ('X_train.shape={}\n y_train.shape ={}\n X_test.shape={}\n, y_test.shape={}'.format(X_train.shape,y_train.shape, X_test.shape,y_test.shape))
linreg = LinearRegression()
model=linreg.fit(X_train, y_train)
print (model)
# 训练后模型截距
print (linreg.intercept_)
# 训练后模型权重(特征个数无变化)
print (linreg.coef_) feature_cols = ['中证500','泸深300','上证50','上证180','上证指数']
B=list(zip(feature_cols,linreg.coef_))
print(B)3、模型预测
#预测
y_pred = linreg.predict(X_test)
print (y_pred) #10个变量的预测结果4、模型评估
#评价
#(1) 评价测度
# 对于分类问题,评价测度是准确率,但这种方法不适用于回归问题。我们使用针对连续数值的评价测度(evaluation metrics)。
# 这里介绍3种常用的针对线性回归的测度。
# 1)平均绝对误差(Mean Absolute Error, MAE)
# (2)均方误差(Mean Squared Error, MSE)
# (3)均方根误差(Root Mean Squared Error, RMSE)
# 这里我使用RMES。
sum_mean=0
for i in range(len(y_pred)):
sum_mean+=(y_pred[i]-y_test.values[i])**2
sum_erro=np.sqrt(sum_mean/10) #这个10是你测试级的数量
# calculate RMSE by hand
print ("RMSE by hand:",sum_erro)
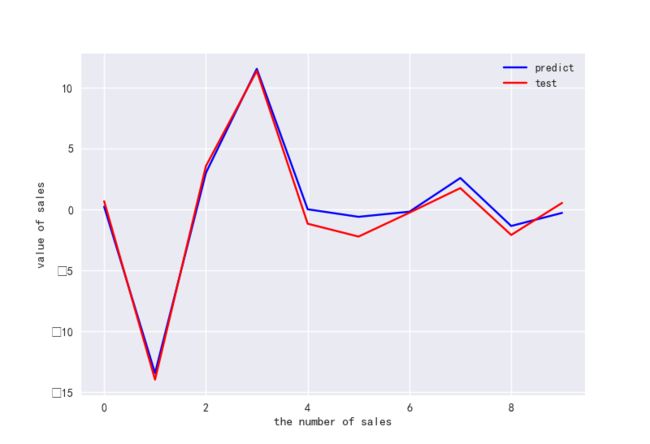
#做ROC曲线
plt.figure()
plt.plot(range(len(y_pred)),y_pred,'b',label="predict")
plt.plot(range(len(y_pred)),y_test,'r',label="test")
plt.legend(loc="upper right") #显示图中的标签
plt.xlabel("the number of sales")
plt.ylabel('value of sales')
plt.show()附录:
相应的参数说明。
fit_intercept: 布尔型,默认为true
说明:是否对训练数据进行中心化。如果该变量为false,则表明输入的数据已经进行了中心化,在下面的过程里不进行中心化处理;否则,对输入的训练数据进行中心化处理
normalize布尔型,默认为false
说明:是否对数据进行标准化处理
copy_X 布尔型,默认为true
说明:是否对X复制,如果选择false,则直接对原数据进行覆盖。(即经过中心化,标准化后,是否把新数据覆盖到原数据上)
**n_jobs整型, 默认为1
说明:计算时设置的任务个数(number of jobs)。如果选择-1则代表使用所有的CPU。这一参数的对于目标个数>1(n_targets>1)且足够大规模的问题有加速作用。
返回值:
coef_ 数组型变量, 形状为(n_features,)或(n_targets, n_features)
说明:对于线性回归问题计算得到的feature的系数。如果输入的是多目标问题,则返回一个二维数组(n_targets, n_features);如果是单目标问题,返回一个一维数组 (n_features,)。
intercept_ 数组型变量
说明:线性模型中的独立项。
注:该算法仅仅是scipy.linalg.lstsq经过封装后的估计器。
方法:
decision_function(X) 对训练数据X进行预测
fit(X, y[, n_jobs]) 对训练集X, y进行训练。是对scipy.linalg.lstsq的封装
get_params([deep]) 得到该估计器(estimator)的参数。
predict(X) 使用训练得到的估计器对输入为X的集合进行预测(X可以是测试集,也可以是需要预测的数据)。
score(X, y[,]sample_weight) 返回对于以X为samples,以y为target的预测效果评分。
set_params(**params) 设置估计器的参数
decision_function(X) 和predict(X)都是利用预估器对训练数据X进行预测,其中decision_function(X)包含了对输入数据的类型检查,以及当前对象是否存在coef_属性的检查,是一种“安全的”方法,而predict是对decision_function的调用。
score(X, y[,]sample_weight) 定义为(1-u/v),其中u = ((y_true - y_pred)**2).sum(),而v=((y_true-y_true.mean())**2).mean()
最好的得分为1.0,一般的得分都比1.0低,得分越低代表结果越差。
其中sample_weight为(samples_n,)形状的向量,可以指定对于某些sample的权值,如果觉得某些数据比较重要,可以将其的权值设置的大一些。
例子:
from sklearn import linear_model
clf = linear_model.LinearRegression()
clf.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
clf.coef_
array([ 0.5, 0.5])参数官网说明