拓扑排序 关键路径的代码实现
问题描述
通常把计划、施工过程、生产流程、程序流程等都当成一个工程。工程通常分为若干个称为“活动”的子工程。完成了这些“活动”,这个工程就可以完成了。通常用AOE-网来表示工程。AOE-网是一个带权的有向无环图,其中,顶点表示事件(EVENT),弧表示活动,权表示活动持续的时间。
AOE-网可以用来估算工程的完成时间。可以使人们了解:
(1)研究某个工程至少需要多少时间?
(2)哪些活动是影响工程进度的关键?
由于AOE-网中的有些活动可以并行进行,从开始点到各个顶点,以致从开始点到完成点的有向路径可能不止一条,这些路径的长度也可能不同。完成不同路径的活动所需的时间虽然不同,但只有各条路径上所有活动都完成了,这个工程才算完成。因此,完成工程所需的最短时间是从开始点到完成点的最长路径的长度,即在这条路径上的所有活动的持续时间之和.这条路径长度就叫做关键路径(Critical Path)。
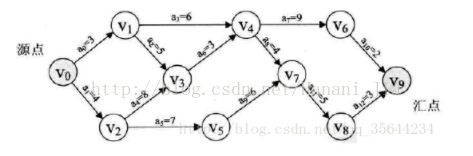
例:AOE图如下:
程序执行结束后应该输出:
关键活动为a1,a4,a7,a10,a8,a11
关键路径为: a1->a4->a7->a10(或者V1->V2->V5->V7->V9)和a1->a4->a8->a11(或者V1->V2->V5->V8->V9)
花费的时间为至少为18(时间单位)。
一. 算法设计
由于在AOE-网中有些活动是可以并行进行的,所以完成工程的最短时间是从开始点到完成点的最长路径的长度。路径长度最长的路径叫做关键路径。假设开始点是v1,从v1到vi的最长路径长度叫做事件vi的最早发生时间。这个时间决定了所有以vi为尾的弧所表示的活动的最早开始时间l(i),这是在不推迟整个工程完成的前提下,活动ai最迟必须开始进行的时间,两者之差l(i)-e(i)意味完成活动ai的时间余量。我们把l(i)=e(i)的活动叫做关键活动。显然关键路径上的所有活动都是关键活动,因此提前完成非关键活动并不能加快工程的进度。例如上图网中从v1到v9的最长路径长度为18,即v9的最早发生时间是18.而活动a6的最早开始时间是5,最迟开始时间是8,这意味着,如果a6
推迟三天或者延迟三天完成都不会影响整个工程的完成。因此,分析关键路径的目的是辨别哪些是关键活动,以便争取提高 关键活动的功效,缩短整个工期。
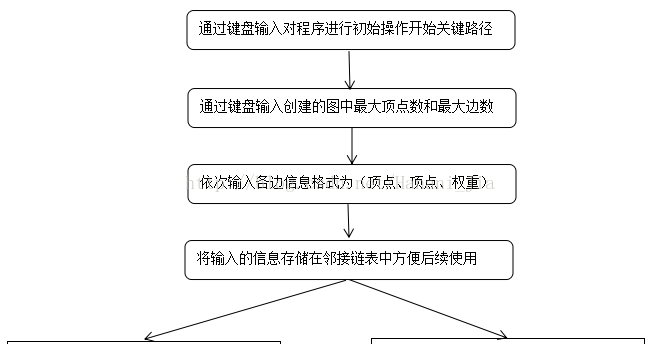
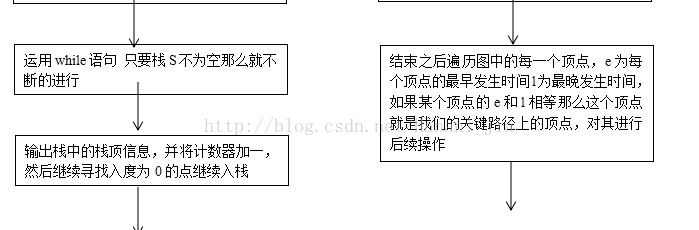
因此辨别关键活动就是要去找e(i)=l(i)的活动。为了求得网中的活动首先求的所有活动的最早发生时间和最晚发生时间。从前往后推来求得最早发生时间,之后再从后往前推求得最晚发生时间。程序开始输入你所要创建的图的顶点和弧,建立网的存储结构。之后一次输入图中的所有顶点。再一次从键盘输入两个顶点之间的权重。用邻接链表的存储方式来存储这个带权有向图,结构体中包含图的顶点数和边的数目,包含每个节点的入度方便求拓扑排序,包含人为设定标志点,方便后期判断是否存在两条不同的最短路径,通过键盘输入创建图的邻接链表,先将各个顶点存入数组,之输入边,方式为输入两个顶点,之后输入两个顶点之间的权重。将存储的图拓扑排序,创建一个栈,将入度为0的顶点存入栈,当栈里的元素输出的时候,这些元素所指向的元素的入度减去一,当存在入度为0的元素的时候继续进栈,当最终栈为空的时候终止循环即可。将创建好的邻接链表正向求解,求出每个活动的最早发生时间,如果当前路径小于之前所求的路径进行更换,之后逆向邻接链表求出每个活动的最晚发生时间,将两个时间分别存储在对应的Ve和Vl数组中,然后将两个数组对应的进行相减如果求得的数为0那么该活动就是这个工程的关键活动。之后将求得的关键路径和关键活动进行输出即可。
二. 算法实现
1. 操作系统:win 10 运行环境 :vs2013
2. 流程图
3.代码实现
#define _CRT_SECURE_NO_WARNINGS 1
#include
#include
#include
#define MaxVernum 20 //定义图最大顶点数目
#define STACK_INIT_SIZE 10 //存储空间初始分配量
#define STACKINCREMENT 2 //存储空间分配增量
int degree[MaxVernum];
typedef int SElemType;
typedef char VertexType;
//存储图的边
typedef struct ArcNode
{
SElemType Ver;//存储边所指向的顶点
SElemType Weight;//存储该边的权重
struct ArcNode *next;//指向下一个边的指针结点
}ArcNode;
//存储图的顶点
typedef struct VerNode
{
VertexType data[20];//存储该顶点的数据
struct ArcNode *firstArc;// 边的头指针
SElemType indegree;//该结点的入度
SElemType flag;//设定一个标志用于后期判断最短路径是一条还是多条
}VerNode, AdjList[MaxVernum];
//存储图
typedef struct
{
AdjList adjlist;
SElemType Arcnum;//存储图中的边的数目
SElemType Vernum;//存储图中的顶点的数目
}ALGraph;
//栈的顺序存储结构表示
typedef struct SqStack
{
SElemType *base; //栈底地址
SElemType *top; //栈顶指针
int stacksize; //当前已经分配的存储空间
}SqStack;
//构造一个空栈
int InitStack(SqStack &S)
{
//为栈底分分配一个指定大小的存储空间
(S).base = (SElemType *)malloc(STACK_INIT_SIZE*sizeof(SElemType));
if (!(S).base)
exit(0);
(S).top = (S).base; //栈底与栈顶指针相同
(S).stacksize = STACK_INIT_SIZE;
return 1;
}
//若栈S为空栈(栈底指针和栈顶指针相同), 则返回1,否则返回0
int StackEmpty(SqStack S)
{
if (S.top == S.base)
return 1;
else
return 0;
}
//插入元素e为新的栈顶元素
int Push(SqStack *S, SElemType e)
{
if ((*S).top - (*S).base >= (*S).stacksize)
{
(*S).base = (SElemType *)realloc((*S).base, ((*S).stacksize + STACKINCREMENT)*sizeof(SElemType));
if (!(*S).base)
exit(0);
(*S).top = (*S).base + (*S).stacksize;
(*S).stacksize += STACKINCREMENT;
}
*((*S).top)++ = e;
return 1;
}
//若栈不为空,则删除S栈顶元素用e返回其值,并返回1,否则返回0
int Pop(SqStack *S, SElemType &e)
{
if ((*S).top == (*S).base)
{
return 0;
}
e = *--(*S).top;
return 1;
}
void Finedegree(ALGraph *G)
{
int j = 0;
for (j = 0; jVernum; j++)
{
degree[j] = G->adjlist[j].indegree;
//printf("第%d个顶点即%c入度为:%d\n", j + 1, G->adjlist[j].data, degree[j]);
}
}
//有向图的G采用邻接表存储结构,若G无回路,则输出G的顶点的一个拓扑结构
int TopologicalSort(ALGraph *G)
{
int i, k;
int count = 0;
SqStack S;
ArcNode *p;
int e = 0;
int j = 0;
p = NULL;
InitStack(S);
Finedegree(G);
for (i = 0; iVernum; i++)
{
if (!degree[i])
Push(&S, i);//把入度为零的节点压栈
}
printf("拓扑排列如下:\n");
while (!StackEmpty(S))//只要栈不是空的就一直进行
{
Pop(&S, i);//栈不是空的那就将里边的一个出栈然后输出
printf("%s", G->adjlist[i].data);
count++;
for (p = G->adjlist[i].firstArc; p; p = p->next)
{
k = p->Ver;
if (!(--degree[k]))
Push(&S, k);
}
}
if (count < G->Vernum)
{
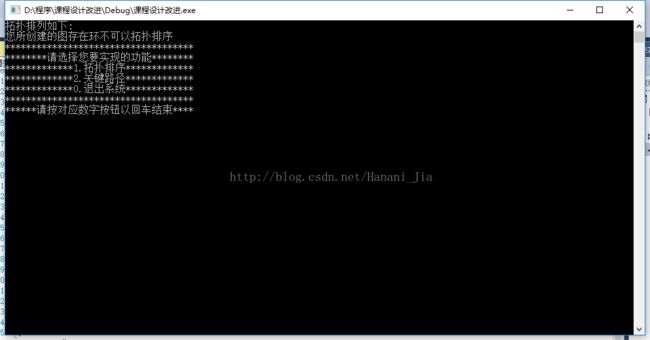
printf("您所创建的图存在环不可以拓扑排序");
return 0;
}
printf("\n");
return 0;
}
int IfArc(ALGraph *G, char *a)//检查用户再次输入顶点是否在图中
{
int i = 0;
for (i = 0; i < G->Vernum; i++)
{
if (!strcmp(a, G->adjlist[i].data))
return i;//如果输入的顶点和图中某一顶点数值相同返回该顶点在图中的位置,return i之后就不会再执行函数之后的内容
}
return -1;//如果for循环结束之后还没有找到对应的值那么函数返回值为-1
}
//构造函数 创建图
void CreateALGraph(ALGraph *G)
{
char v1[20];
char v2[20];
int i = 0;
int w = 0;
int m = 0;
int n = 0;
ArcNode *p;
printf("请输入你想组建图的顶点总数和弧边总数:\n");
scanf("%d %d", &G->Vernum, &G->Arcnum);
for (i = 0; i < G->Vernum; i++)//初始化图中的顶点信息
{
fflush(stdin);//清空缓存区以免将上一步的空格回车等信息输入
printf("请输入第%d个顶点", i + 1);
scanf("%s", &G->adjlist[i].data);//给所有顶点数据进行初始化
G->adjlist[i].firstArc = NULL;//将每个顶点的头指针,以及入度初始化
G->adjlist[i].flag = 0;
G->adjlist[i].indegree = 0;
}
system("cls");
for (i = 0; i < G->Arcnum; i++)//初始化图中的弧边信息
{
fflush(stdin);
printf("请输入两顶点以及之间的权重(v1,v2,w):\n");
printf("a%d:", i + 1);
scanf("%s %s %d", &v1, &v2, &w);
m = IfArc(G, v1);
n = IfArc(G, v2);
if (m == -1 || n == -1)//只要其中任何一个顶点不在图中要求重新输入
{
i = i - 1;//因为这次输入数据错误所以将i减去1,不增加循环次数
printf("输入顶点数据错误请重新输入\n");//输出错误信息
continue;//跳过本次循环不再对边的其他内容进行操作
}
p = (ArcNode*)malloc(sizeof(ArcNode));//对p进行空间分配分配的大小是一个ArcNode结构体的大小
p->Ver = n;//顶点信息
p->Weight = w;//权重信息
p->next = G->adjlist[m].firstArc;//将刚刚输入的两个顶点链接起来
G->adjlist[m].firstArc = p;
G->adjlist[n].indegree++;
}
system("cls");
}
//求关键路径、关键活动函数
void FineCriticalpath(ALGraph *G, SqStack &T)
{
char first[20];
char end[20];
int sum = 0;
int *Ve;
int *Vl;
int i = 0;
int k = 0;
int e = 0;
int l = 0;
int max = 0;
int count = 0;
int j = 0;
int spend = 0;
SqStack S;
ArcNode *p;
p = NULL;
Ve = (int *)malloc(sizeof(int)*G->Arcnum);
Vl = (int *)malloc(sizeof(int)*G->Arcnum);//给两个数组分配内存空间,有Arcnum个边一个边占int大小的字节
memset(Ve, 0, G->Arcnum);
memset(Vl, 0, G->Arcnum);//对两个数组进行初始化
InitStack(S);
InitStack(T);
Finedegree(G);
for (i = 0; iVernum; i++)
{
if (!degree[i])
Push(&S, i);//把入度为零的节点压栈
}
printf("拓扑排列如下:\n");
while (!StackEmpty(S))//只要栈不是空的就一直进行
{
Pop(&S, i);//栈不是空的那就将里边的一个出栈然后输出
sum++;
if (sum==1)
strcpy(first, G->adjlist[i].data);
if (sum==G->Vernum)
strcpy(end, G->adjlist[i].data);
Push(&T, i);
printf("%s", G->adjlist[i].data);
count++;
for (p = G->adjlist[i].firstArc; p; p = p->next)
{
k = p->Ver;
if (!(--degree[k]))
Push(&S, k);
if (Ve[i] + p->Weight>Ve[k])//如果前结点的最早开始时间加上权重大于后结点的最早开始时间
Ve[k] = Ve[i] + p->Weight;//那么就把厚结点的开始时间换成前结点的时间加权重
}
}
if (count < G->Vernum)
{
printf("您所创建的图存在环不可以拓扑排序\n");
return;
}
printf("\n");
for (i = 0; i < G->Vernum; i++)
{
Vl[i] = Ve[G->Vernum - 1];
}//把求得的最早开始时间存到最晚开始时间的数组
while (!StackEmpty(T))
for (Pop(&T, i), p = G->adjlist[i].firstArc; p; p = p->next)
{
k = p->Ver;//为了获得当前顶点在图中的位置来存储最早开始时间
if (Vl[k] - p->Weight < Vl[i])//如果最晚发生时间中的减去相应的权重之后比最早发生时间要小
Vl[i] = Vl[k] - p->Weight;//就要将最晚发生时间进行替换
}
for (i = 0; i < G->Vernum; i++)
for (p = G->adjlist[i].firstArc; p; p = p->next)
{
k = p->Ver;
e = Ve[i];
l = Vl[k] - p->Weight;//求每个活动的最早发生时间和最晚发生时间并且输出
printf("顶点%s 与顶点%s 活动的最早发生时间为%d 活动的最晚发生时间为%d\n", G->adjlist[i].data, G->adjlist[k].data, e, l);
}
printf("\n");
printf("该工程起点为%s\n",first);
printf("该工程终点为%s\n", end);
printf("\n");
for (i = 0; i < G->Vernum; i++)
{
p = G->adjlist[i].firstArc;
while (p)
{
k = p->Ver;
e = Ve[i];
l = Vl[k] - p->Weight;
if (e == l)//如果相同才是关键活动
{
G->adjlist[i].flag++;//标记已经输出过了下次在输出就要加括号
if (G->adjlist[i].flag == 1)
{
spend = spend + p->Weight;
printf("(关键活动为%s------>%s 路径长度为%d)\n", G->adjlist[i].data, G->adjlist[k].data, p->Weight);
}
else
{
G->adjlist[k].flag++;
if (G->adjlist[i].flag > max)
{
max = G->adjlist[i].flag + 1;
}
printf("(第%d条关键活动为%s------>%s 路径长度为%d)\n", G->adjlist[i].flag, G->adjlist[i].data, G->adjlist[k].data, p->Weight);
}
}
p = p->next;
}
}
printf("\n");
printf("本次工程共有%d条关键路径\n", max);
printf("\n");
printf("本次工程花费的最少时间为:%d\n", spend);
printf("\n");
}
void menu()
{
printf("************************************\n");
printf("********请选择您要实现的功能********\n");
printf("*************1.拓扑排序*************\n");
printf("*************2.关键路径*************\n");
printf("*************0.退出系统*************\n");
printf("************************************\n");
printf("******请按对应数字按钮以回车结束****\n");
}
int main()
{
int set = 0;
ALGraph G;
SqStack T;
menu();
scanf("%d", &set);
while (set)
{
switch (set)
{
case 1:
CreateALGraph(&G);
TopologicalSort(&G);
break;
case 2:
CreateALGraph(&G);
FineCriticalpath(&G, T);
break;
default:
printf("输入错误请重新输入\n");
break;
}
menu();
scanf("%d", &set);
}
system("pause");
return 0;
}
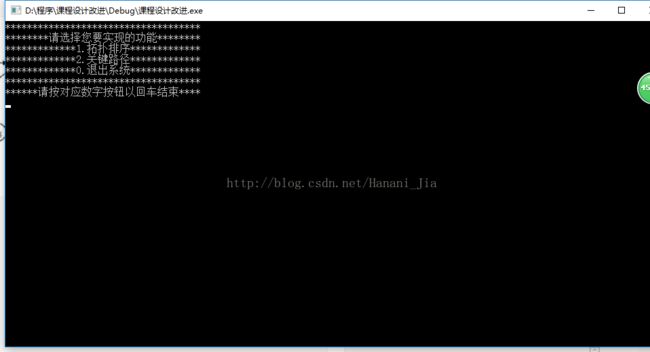
4.程序过程截图
运行示例图:
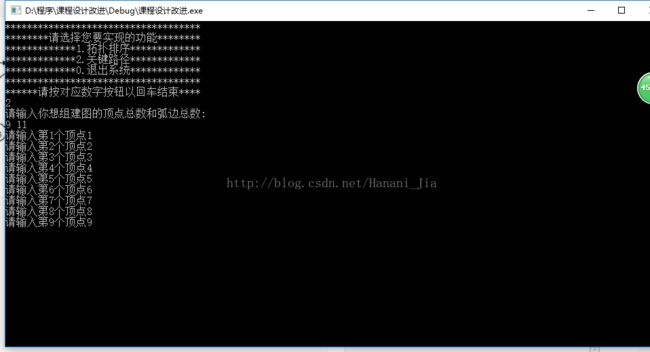
第一步:选择想要实现的程序功能
第二步:输入创建的图的顶点数和弧边数,并依次输入各个顶点的信息
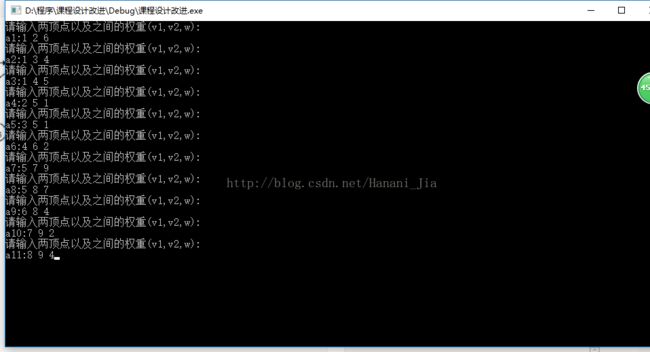
第三步:输入边的信息格式为顶点、顶点、两顶点之间的权重。
第四步:输出程序求解情况
判断所输出的图有环情况