Semi-Global Matching (SGM)
一. Matching cost computation
SGM的第一步也是代价计算,它采用了基于互信息的计算方法,互信息是一种熵。
熵是用来表征随机变量的不确定性(可以理解为变量的信息量),不确定性越强那么熵的值越大(最大为1),那么图像的熵其实就代表图像的信息量。互信息度量的是两个随机变量之间的相关性,相关性越大,那么互信息就越大。两幅图像如果匹配程度非常高,说明这两幅图像相关性非常大!反之,如果两幅图像配准程度很低,那么两幅图像的互信息就会非常小。所以,立体匹配的目的当然就是互信息最大化。这就是为什么使用互信息的原因。
熵和互信息的定义分别如下所示:

![]()
其中,互信息的前两项是图像的熵,最后一项叫做联合熵,联合熵是熵的变种,其依赖的自然是联合概率分布(熵依赖的是概率分布),联合熵的公式如下所示:

这时,一个最自然的问题是,图像的概率分布P是什么意思?答案一句话,图像的灰度直方图。图像的灰度值是 0 ∼ 255 0\sim255 0∼255,每个灰度值对应的像素个数除以图像像素个数就是该灰度值对应的概率,单幅图像的概率密度是一维的,那么自然地,两幅图像的联合概率密度就是二维的,它的定义域取值就是 ( 0 , 0 ) ∼ ( 255 , 255 ) (0,0)\sim(255,255) (0,0)∼(255,255),公式如下所示:

其中, ( i , k ) (i,k) (i,k) 指的是像素灰度值时, l 1 l1 l1和 l 2 l2 l2 分别代表了左图和矫正之后的右图, p p p代表像素点, n n n代表着像素的总数,公式的含义是统计不同灰度值对的个数并归一化。因此,俩副图像对应的概率分布可以用一幅图表示,这幅图的大小一定是 256 × 256 256\times256 256×256,即联合概率分布就是归一化之后的统计直方图。
弄清楚了概率分布P的含义,作者引用了其他文献的研究成果,先说了联合熵的定义,直接用泰勒展开近似联合熵为像素和的形式,如下所式:

其中,作者称 h h h为数据项,自变量为像素灰度值,所以可以事先建立一个查表,将每个灰度值对的 h h h保存下来(一共 256 × 256 256\times256 256×256),那么联合熵的计算速度就会很快, h h h的计算公式如下所示:

其中, g ( i , k ) g(i,k) g(i,k)指的是高斯平滑,P是一副表征概率值的图像(分辨率恒为 256 × 256 256\times256 256×256),正是针对这幅图像进行平滑处理,但是作者在这里称之为Parzen估计,Parzen是一种非参数估计方法,不需要事先假设数学模型的参数形式而直接估计单点的概率值,最常用的Parzen窗函数就是高斯核函数。作者提供了一个图示也可以说明这个问题:
 其中,第一个坐标系就是联合概率分布图,由于事先要对匹配图像(一般是右图)基于视差图进行修正(warp),调整右图像素的位置,使得左右俩图尽可能相同之后计算同一像素位置的联合概率,由此导致了诸如(10,10),(25,25),(125,125)这样的灰度值对应的概率值更大一些。再对这样的7x7窗口大小的高斯平滑处理,高斯平滑的目的是消除噪声,因为这里基于的视差图是很粗糙的(只有非遮挡点才有视差值,遮挡点的视差都为0),根据这样的视差图对右图进行处理,难免一些位置所对应的俩图灰度值不相等,体现在P图就是噪声,这时候当然要平滑。例如有可能出现(10,100)这样的灰度值,这说明右图该点经过warp之后很可能是错误的,但是这种情况肯定是少数,对应的概率值也就是很小,体现在P图上就是噪声。其实这就是检测outlier,去除outlier的另外一种手段,只不过SGM是从概率分布的角度处理罢了,而其他的算法一般都是从空间分布来处理outlier。进一步,取负对数便得到了h值的图示,最后得到了图像的联合熵图。
其中,第一个坐标系就是联合概率分布图,由于事先要对匹配图像(一般是右图)基于视差图进行修正(warp),调整右图像素的位置,使得左右俩图尽可能相同之后计算同一像素位置的联合概率,由此导致了诸如(10,10),(25,25),(125,125)这样的灰度值对应的概率值更大一些。再对这样的7x7窗口大小的高斯平滑处理,高斯平滑的目的是消除噪声,因为这里基于的视差图是很粗糙的(只有非遮挡点才有视差值,遮挡点的视差都为0),根据这样的视差图对右图进行处理,难免一些位置所对应的俩图灰度值不相等,体现在P图就是噪声,这时候当然要平滑。例如有可能出现(10,100)这样的灰度值,这说明右图该点经过warp之后很可能是错误的,但是这种情况肯定是少数,对应的概率值也就是很小,体现在P图上就是噪声。其实这就是检测outlier,去除outlier的另外一种手段,只不过SGM是从概率分布的角度处理罢了,而其他的算法一般都是从空间分布来处理outlier。进一步,取负对数便得到了h值的图示,最后得到了图像的联合熵图。
其实,平滑归平滑,也只是基于256*256的图像进行平滑,只需根据像素位置计算出权重即可,同样可以根据查表的方式实现,这和具体的双目图像大小仍旧无关,一个不小的优点哦!
作者为什么要用互信息来计算代价匹配值?根据文献给出的信息,作者是考虑到了互信息对光照具有鲁棒性,互信息越大->相关性越大->俩个点的匹配程度越高->代价计算值理应越小:

(由于互信息越大,相关系越大,取负数后,代价计算理应越小。)
大家有没有觉得作者在此处的思维很是特别?先根据一个视差图作为先验来确定互信息图,然后基于这样的互信息图去计算各个视差的代价,这在理论上显然会导致第一步得到的视差图非常近似于初始视差图。
本来熵和联合熵的计算方法不同,但是由于遮挡点的问题,将二者设置成相同的,都采用泰勒近似的方式。具体来说,图像的熵是基于图像的概率分布来计算的,但由于遮挡点的存在,有些像素根本不会有匹配点,如果也将这样的像素考虑在内恐怕不合适,别忘了我们的目的是令能够匹配的点尽量匹配,不能匹配的点根本没有必要匹配,于是放在了联合熵的定义,联合熵是基于联合概率分布的,起基于的点可以保证都是匹配点,这样的概率公式如下表示:
![]()
进一步,基于这样的概率分布得到的图像熵公式如下所示:

最后,作者采用分层信息(HMI)进行代价匹配计算,由于概率分布图和图像大小无关(一直都是 256 × 256 256 \times 256 256×256),所以可以采用分层计算的方式来加速(反正不同层都是 256 × 256 256 \times 256 256×256),每一层的计算对应一次迭代,别忘记首次迭代需要给基于是视差图对右图进行warp,没有视差图怎么办?文章是说随机生成就好,并且由于像素个数跟多,随机生成的个别错误可以被容忍,warp之后的右图和左图的匹配程度还是会比较高,迭代次数也相对较低,这也是SGM的一大优点。
作者还对HMI的时间复杂度进行了计算,由于单次迭代的时间复杂度是O(WHD),W指图像的width,H指图像的height,D应该是指迭代次数。
二. Cost aggregation
SGM的代价聚合,其实仔细看看,这并不是严格意义上的代价聚合,因为SGM是为了优化一个能量函数,这和一般的全局算法一样,如何利用优化算法求解复杂的能量函数才是重中之重,其能量函数如下所示:

其中, C ( p , D p ) C(p, D_{p}) C(p,Dp) 代表的就是基于互信息的代价计算项,后面俩项值指的是当前像素p和其领域内所有像素q之间的约束,如果q和p的视差只差了1,那么惩罚P1,如果大于1,那么惩罚P2,这么做基本上是机器学习中的常用方法,即所谓的正则化约束。需要注意的是,P2要大于P1。
1.假如不考虑像素之间的制约关系,不假设领域内像素应该具有相同的视差值,那么最小化 E ( D ) E(D) E(D)就是最小化每一个C,这样的视差图效果很差,因为图像总会受到光照,噪声等因素的影响,最小的代价对应的视差往往是“假的“,并且这样做全然不考虑相邻之间的像素关系。例如,一个桌面的视差明显应该相同,但是可能由于倾斜光照的影响,每个像素的最小代价往往会不同,东一块西一块的,这就是加上约束的目的。
2.添加俩个正则化项一方面是为了保证视差图平滑,另一方面是为了保持边缘(保持边缘一直没想明白为什么?)。惩罚越大,说明越不想看到这种情况发生,具体来说,如果q和p之间的视差有所差异但又不大,那么就要付出代价,你不是想最小化能量函数么?那么二者都要小,如果没有第二项,那么求出来的视差图会有明显的锯齿现象,如果只有第三项,那么求出来的视差图边缘部分将会保持,但是由于没有对相差为1的相邻像素进行惩罚,物体内部很可能出现一个"斜面"。
3.文章有对这俩项的解释,内容为: 有了能量函数,下面要做的就是求解它了,这个时候问题来了,这个E对p是不可导的,这意味着我们常看到的梯度下降,牛顿高斯等等算法在这里都不适用,作者于是采用了动态规划来解决这一问题。简单的说,就是p的代价函数想要最小,那么前提是必须是领域内的点q代价最小,q想要代价最小,那么必须保证q的领域点m的代价最小,如此传递下去。 本文只说说作者是怎么利用动态规划来求解E,其实这个求解问题是NP完全问题,想在2D图像上直接利用动态规划求解是不可能的,只有沿着每一行或者每一列求解才能够满足多项式时间(又叫做扫描线优化),但是这里问题来了,如果我们只沿着每一行求解,那么行间的约束完全考虑不到,q是p的领域的点其实这个时候被弱化到了q是p的左侧点或者右侧点,这样的求优效果肯定很差。于是,大招来了!!我们索性不要只沿着横或者纵来进行优化,而是沿着一圈8个或者16个方向进行优化。 其实为什么分解为8个方向想想看也很正常,能量函数E中每个p的能量是“自身代价本身+周围像素q带来的惩罚”,周围像素足足有8个,想求它们和的最小化十分难,最朴素的想法就是“分而求之”,我们就规定一个方向r,这个方向上p的邻居q只有一个,那么沿着这一方向的p的代价聚合值就成为了上面公式的样子。进一步,将8个方向的代价聚合值都加起来,就形成了p的最终代价聚合值。然后用WTA搞一下得到的视差图可以得到一个较小的能量E,目的就达到了。 对左图计算完视差图后,还可以以同样的方法来对右图进行视差图的计算,在将二者融合起来。也可以利用多个立体像对来计算多张稠密视差图。 对左图计算一个视差图后,也可对右图计算一个视差图。然后进行一致性校验。 采用联通域分割法,将视差相差在1个像素以内的像素4邻域归为一个联通域来分割所得的视差图。 这步是SGM后处理比较核心的一步。 室内环境中,后景常常为无纹理区域,如墙等。为解决这个问题,先提出以下三个假设: 解决步骤: 先对图像进行分割,得到前后景区域。问题就变为如何正确选择后景(无纹理区域)的边界和视差,较好的分割出前景物体。 对于后景,作者做了两个假设:一是其为一个较大的均匀区域,内部梯度变化很小;二是这是一个平面。对于深度变化(物体边界),作者的假设为前后景的外观不一致,因此二者之间存在较大的梯度。 后处理完的视差图可能因为遮挡或误匹配而存在缺失区域。对这些区域的视差进行插值前要对其性质进行分类,以使用不同的插值方法: 注意:对与遮挡相连的误匹配区域,同样利用背景像素进行外插值。
 这句话隐含的意思是,如果我们让P1
这句话隐含的意思是,如果我们让P1

我们先来看看优化求解过程:


每一个点的代价聚合值是“当前代价+min(路径相邻点的当前视差代价聚合值,路径相邻点的视差差值为1的代价聚合值 + P1,路径相邻点的视差插值大于1的最小代价聚合值 + P2)- 路径相邻点的视差插值大于1的最小代价聚合值 ”,听起来够绕口的,其实就好比最小代价的蔓延,当前代价聚合值由当前代价和路径上一点的加了惩罚的最小代价聚合值所决定(最后那一项纯粹是为了防止数字过大,这是常用手段)。三. Multi-baseline matching
四. Disparity Refinement
1.移除极值
根据场景事先确定一个大小阈值,去除像素数量过少的联通域。2.Intensity Consistent Disparity Check
室内场景的前后景之间会有视差不连续,但前述的能量方程对于发生视差不连续的位置没有偏好,这种不连续可能在错误的地方出现,因此会造成错误的前后景物体边界,或者一个斜面。
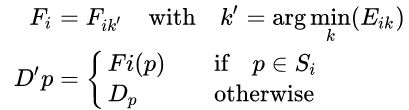
3.Discontinuity Preserving Interpolating
1.遮挡:用背景的视差进行外插值,而不使用前面的遮挡物的视差;
2.误匹配:可以利用其周围的像素进行插值。整体流程图为:
