非监督学习之PCA降维&流行学习TSNE

作者：徐莹

1.PCA简介

使用非监督学习的方式进行数据变换有非常广泛的用途。最常见的目的就是对数据进行可视化，将数据进行压缩并为进一步处理得到一个更有效的数据表示。这其中最有效使用最广泛的技术要数PCA（Principal Component Analysis）了。

主成分分析（PCA）是一种以某种方式旋转数据集的方法，使得旋转特征在统计学上不相关。这种旋转通常是根据它们能够解释数据的能力的重要性来选择新特征的子集。

第一个图显示原始数据点，着色以区分点。算法首先找出最大方差的方向，标记为“分量1“。这是数据中包含大多数信息的方向，或者换句话说，这是每一个特征最相关的方向。然后，算法找到与第一方向正交（在直角）时包含最多信息的方向。在二维空间中，只有一个可能的方向是直角，但是在高维空间中会有无穷多个正交方向。通过这种方式找到的方向称之为“Principal Component”，它代表了数据方差的主要方向。

第二个图显示相同的数据，但现在旋转，使得第一主成分与x轴对齐，第二主成分与y轴对齐。在旋转之前，从数据中减去平均值，使得变换数据以零为中心。在PCA发现的旋转表示中，两个轴是不相关的，这意味着该表示中的数据的相关矩阵，除了对角线之外是零。我们可以通过只保留一些主成分来使用PCA进行维数约简。在这个例子中，我们可能只保留第一个主成分，如图三显示。

这将数据从二维数据集减少到一维数据集。但我们只保留了其中的一个特征，我们发现最有趣的方向（在第一个图的左上到右下）并保持这个方向，第一主成分。

最后，我们可以撤消旋转，并将均值返回到数据。这将产生最后一个图显示的数据。这些点在原始特征空间中，但我们只保留第一主成分中包含的信息。这种转变有时用于去除数据中的噪声效应，或可视化保存在主成分分析中的部分信息。

---

2.PCA实例

PCA 最常见的作用就是对高维数据进行可视化。我们将针对一个乳腺癌的数据集举例。 在进行PCA处理之前，首先对数据进行scale 处理，通过StandardScaler使得数据的每一个特征都有单位方差。

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
scaler = StandardScaler()
scaler.fit(cancer.data)
X_scaled = scaler.transform(cancer.data)

接下来通过fit方法找到 principal components， 通过transform方法进行旋转和维度约减：

from sklearn.decomposition import PCA

# keep the first two principal components of the data
pca = PCA(n_components=2)

# fit PCA model to beast cancer data
pca.fit(X_scaled)

# transform data onto the first two principal components
X_pca = pca.transform(X_scaled)
print("Original shape: %s" % str(X_scaled.shape))
print("Reduced shape: %s" % str(X_pca.shape))

Original shape: (569, 30)
Reduced shape: (569, 2)

# plot fist vs second principal component, color by class
plt.figure(figsize=(8, 8))
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=cancer.target, cmap=mglearn.tools.cm, s=60)
plt.gca().set_aspect("equal")

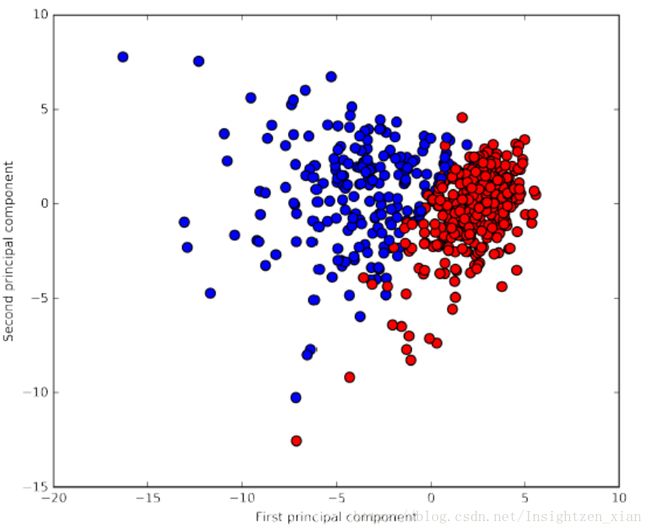
plt.xlabel("First principal component")
plt.ylabel("Second principal component")

PCA 是一种非监督的学习方式，在旋转的过程中不使用任何的分类信息。他只是简单的分析数据之间的相关性。
从图中可以看出，在二维空间中，两类数据被很好地区分开来。

主元存储在 components_ 属性中：pca.components_.shape(2, 30)
components_ 属性的每一行对应一个主元，保存着他们的重要性，每一列对应原始数据的每一个特征。

print(pca.components_)
[[-0.22 -0.1 -0.23 -0.22 -0.14 -0.24 -0.26 -0.26 -0.14 -0.06 -0.21 -0.02
-0.21 -0.2 -0.01 -0.17 -0.15 -0.18 -0.04 -0.1 -0.23 -0.1 -0.24 -0.22
-0.13 -0.21 -0.23 -0.25 -0.12 -0.13]

[ 0.23 0.06 0.22 0.23 -0.19 -0.15 -0.06 0.03 -0.19 -0.37 0.11 -0.09
0.09 0.15 -0.2 -0.23 -0.2 -0.13 -0.18 -0.28 0.22 0.05 0.2 0.22
-0.17 -0.14 -0.1 0.01 -0.14 -0.28]]

---

3.T-SNE简介

虽然PCA能够很好地对数据进行可视化，但是受限于算法的本质，PCA的有效性大打折扣。有一类称为流行学习的可视化的方法，能够承载更复杂的映射提供更好的可视化方法。

T-SNE就是其中最流行的一种。T-SNE的思想是找到数据的一种二维表达方式，同时能够尽可能地保持点与点之间的距离。T-SNE从每个数据点的随机二维表示开始，然后尝试使在原始特征空间中更接近的点更靠近，并且在原始特征空间中相距很远的点更远。T-SNE更强调靠近的点，而不是保存远点之间的距离。换句话说，它试图保存哪些点是彼此相邻的信息。

---

4.T_SNE实例

这里举一个scikit-learn里面的手写数字的数据集的例子，如下图所示可以看到0-9的手写数字图。

代码：

from sklearn.manifold import TSNE
tsne = TSNE(random_state=42)

# use fit_transform instead of fit, as TSNE has no transform method:
digits_tsne = tsne.fit_transform(digits.data)
plt.figure(figsize=(10, 10))
plt.xlim(digits_tsne[:, 0].min(), digits_tsne[:, 0].max() + 1)
plt.ylim(digits_tsne[:, 1].min(), digits_tsne[:, 1].max() + 1)

for i in range(len(digits.data)):
# actually plot the digits as text instead of using scatter
    plt.text(digits_tsne[i, 0], digits_tsne[i, 1], str(digits.target[i]),
    color = colors[digits.target[i]],
    fontdict={'weight': 'bold', 'size': 9})

从图中可以看出，所有的数字类型都被很好地区分开来。