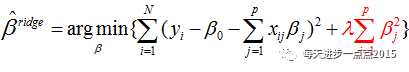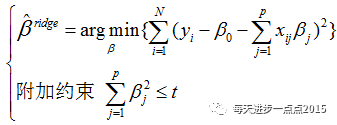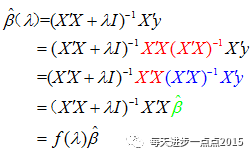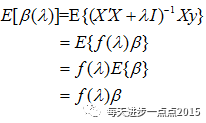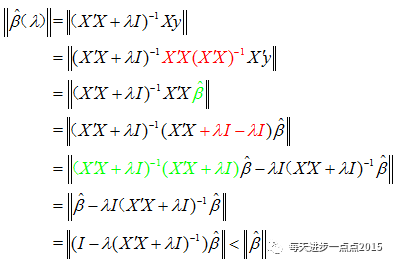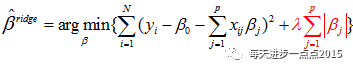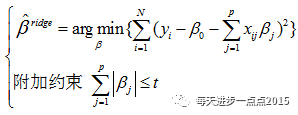岭回归和LASSO回归的区别

问题提出

线性回归模型的偏回归系数的表达式： β=(XTX)−1XTy β = ( X T X ) − 1 X T y

要能保证该回归系数有解，必须确保 XTX X T X 矩阵是满秩的，即 XTX X T X 可逆，但在实际的数据当中，自变量之间可能存在高度自相关性，就会导致偏回归系数无解或结果无效。为了能够克服这个问题，可以根据业务知识，将那些高自相关的变量进行删除；或者选用岭回归也能够避免 XTX X T X 的不可逆。
(岭回归的必要性还有为了防止过拟合)

岭回归一般可以用来解决线性回归模型系数无解的两种情况，一方面是自变量间存在高度多重共线性，另一方面则是自变量个数大于等于观测个数。针对这两种情况，我们不妨设计两个矩阵，来计算一下 XTX X T X 的行列式。
比如：第一种矩阵：第一列和第三列存在两倍关系（即多重共线性）；第二种矩阵：列数比行数多（非满秩）

所以，不管是高度多重共线性的矩阵还是列数多于观测数的矩阵，最终算出来的行列式都等于0或者是近似为0，类似于这样的矩阵，都会导致线性回归模型的偏回归系数无解或解无意义（因为矩阵行列式近似为0时，其逆将偏于无穷大，导致回归系数也被放大）。那如何来解决这个问题呢？1970年Heer提出了岭回归方法，非常巧妙的化解了这个死胡同，即在 XTX X T X 的基础上加上一个较小的 λ λ 扰动 ，从而使得行列式不再为0。

岭回归的参数求解

根据Heer提出的岭回归方法，可以将岭回归系数的求解表达式写成如下这个式子：
β(λ)=(XTX+λI)−1XTy β ( λ ) = ( X T X + λ I ) − 1 X T y

不难发现，回归系数 β β 的值将随着 λ λ 的变化而变化，当 λ=0 λ = 0 时，其就退化为线性回归模型的系数值。

实际上，岭回归系数的解是依赖于下面这个最优化问题

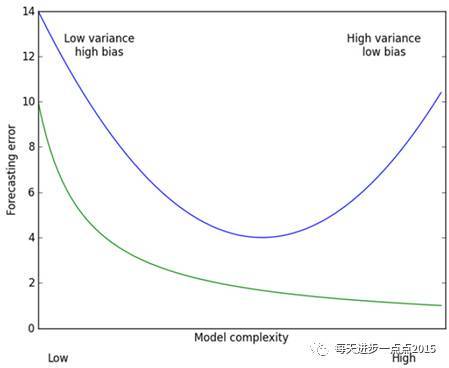
其中，最后一项被称为目标函数的惩罚函数，是一个L2范数，它可以确保岭回归系数beta值不会变的很大，起到收缩的作用，这个收缩力度就可以通过lambda来平衡。之所以用“平衡”这个词，我们可以通过下面这幅图（源于《机器学习实战》）来描述：

这幅图的横坐标是模型的复杂度，纵坐标是模型的预测误差，绿色曲线代表的是模型在训练集上的效果，蓝色曲线代表的是模型在测试集的效果。从预测效果的角度来看，随着模型复杂度的提升，在训练集上的预测效果会越来越好，呈现在绿色曲线上就是预测误差越来越低，但是模型运用到测试集的话，预测误差就会呈现蓝色曲线的变化，先降低后上升（过拟合）；从模型方差角度（即回归系数的方差）来看，模型方差会随着复杂度的提升而提升。针对上面这个图而言，我们是希望平衡方差和偏差来选择一个比较理想的模型，对于岭回归来说，随着lambda的增大，模型方差会减小（因为矩阵X’X行列式在增大，其逆就是减小，从而使得岭回归系数在减小）而偏差会增大。故通过lambda来平衡模型的方差和偏差，最终得到比较理想的岭回归系数。

岭回归的几何意义

上面我们讲解了关于岭回归模型的参数求解，参数解是依赖于一个目标函数，该目标函数还可以表示为：

为什么要添加这个岭回归系数平方和的约束呢？我们知道，岭回归模型可以解决多重共线性的麻烦，正是因为多重共线性的原因，才需要添加这个约束。你可能觉得这说的跟绕口令一样，我们举个例子，也许你就能明白了。例如影响一个家庭可支配收入(y)的因素有收入(x1)和支出(x2)，可以根据自变量和因变量的关系构造线性模型：

y=β0+β1x1+β2x2 y = β 0 + β 1 x 1 + β 2 x 2

假如收入(x1)和支出(x2)之间存在高度多重共线性，则两个变量的回归系数之间定会存在相互抵消的作用。即把beta1调整为很大的正数，把beta2调整为很小的负数时，预测出来的y将不会有较大的变化。所以为了压缩beta1和beta2的范围，就需要一个平方和的约束。

如果把上面的等价目标函数展示到几何图形中的话，将会是（这里以两个变量的回归系数为例）：

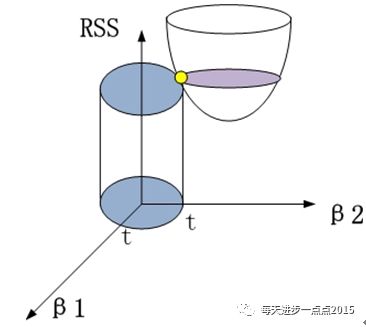
其中，半椭圆体表现的是

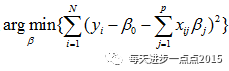
这个目标函数（因为目标函数是关于两个系数的二次函数）；
圆柱体表现的是

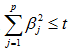
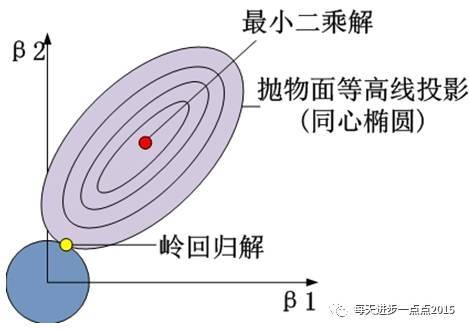
黄色的交点就是满足目标函数下的岭回归系数值。进一步，可以将这个三维的立体图映射到二维平面中，表现的就更加直观了：

岭回归系数的性质

岭回归系数是OLS估计的线性变换

岭回归系数是有偏的

当lambda>0时，岭回归系数具有压缩性

岭参数的选择

我们知道岭回归系数会随着lambda的变化而变化，为保证选择出最佳的岭回归系数，该如何确定这个lambda值呢？一般我们会选择定性的可视化方法和定量的统计方法。对这种方法作如下说明：

1）绘制不同lambda值与对应的beta值之间的折线图，寻找那个使岭回归系数趋于稳定的lambda值；同时与OLS相比，得到的回归系数更符合实际意义；

2）方差膨胀因子法，通过选择最佳的lambda值，使得所有方差膨胀因子不超过10；

3）虽然lambda的增大，会导致残差平方和的增加，需要选择一个lambda值，使得残差平方和趋于稳定（即增加幅度细微）。

LASSO回归

最后我们再来介绍一下LASSO回归，其实该回归与岭回归非常类似，不同的是求解回归系数的目标函数中使用的惩罚函数是L1范数，即

同理，该目标函数也可以转换成：

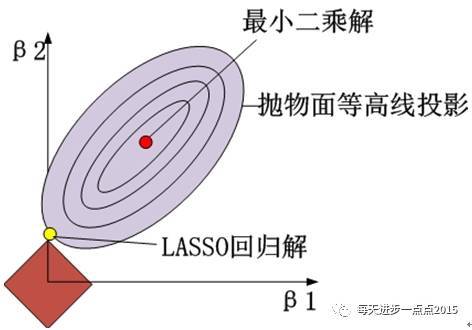
将上面的等价目标函数可以展示到二维几何图形中，效果如下图所示（这里以两个变量的回归系数为例）：

其实，LASSO回归于岭回归只是在惩罚函数部分有所不同，但这个不同却让LASSO明显占了很多优势，例如在变量选择上就比岭回归强悍的多。就以直观的图形为例，LASSO回归的惩罚函数映射到二维空间的话，就会形成“角”，一旦“角”与抛物面相交，就会导致beta1为0（如上图所示），这样beta1对应的变量就是一个可抛弃的变量。但是在岭回归过程中，没有“角”的圆形与抛物面相交，出现岭回归系数为0的概率还是非常小的。