Java数据结构和算法-归并排序的递归应用
归并排序是一种比简单排序快很多的排序算法,在之前介绍的简单排序比如冒泡排序、选择排序的时间都是O(N^2),而归并排序只需要O(N*log(N))的时间,从下图就可以发现归并排序比简单排序要快多少:
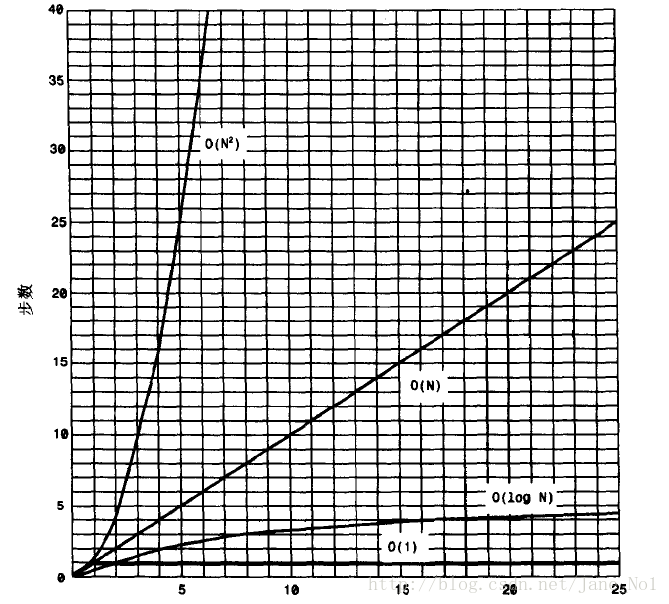
而且归并排序的实现相当容易。它的唯一的缺点就是需要在存储器中有一个与原数组相同大小的数组,如果初始的数组已经几乎占满了整个存储器,那么归并排序将是不可行的,不过如果存储器有足够的空间,那么这将是一个不错的选择。
归并两个有序的数组
归并算法的中心是将两个有序的数组进行归并。比如归并有序数组A和B,将它们复制到数组C中,并且在C中的顺序是有序的。
假设有两个有序数组,不要求大小相同,设A有4个数据项,B也有6个数据项,要将它们归并到数组C中,数组C的初始大小为10。如下图:

图中的小圈内的数组表示复制进C的顺序,过程描述如下表:
| 步骤 | 比较 | 复制 |
|---|---|---|
| 1 | 比较23和7 | 复制7从B到C |
| 2 | 比较23和14 | 复制14从B到C |
| 3 | 比较23和39 | 复制23从A到C |
| 4 | 比较39和47 | 复制39从B到C |
| 5 | 比较47和55 | 复制47从A到C |
| 6 | 比较55和81 | 复制51从B到C |
| 7 | 比较81和62 | 复制62从A到C |
| 8 | 比较81和74 | 复制74从B到C |
| 9 | 复制81从A到C | |
| 10 | 复制95从A到C |
由上表可看出,在第8步之后,数组B的内容已经全部复制到C中,此时A无可比较的内容,所以直接复制到C中即可。
归并部分程序
private void merge(int[] a, int aSize, int[] b, int bSize, int c) {
int aDex = 0, bDex = 0, cDex = 0;
while(aDex < aSize && bDex < bSize)
if(a[aDex] < b[bDex])
c[cDex ++] = a[aDex ++];
else
c[cDex ++] = b[bDex ++];
while(aDex < aSize)
c[cDex ++] = a[aDex ++];
while(bDex < bSize)
c[cDex ++] = b[bDex ++];
} 在程序中进行了三次循环,第一次循环是在两个有序数组中都还有为复制到c的数据项时进行的,在这个循环中,将a和b的数据项进行比较,将将较小者复制到c中;第二、三个循环进行的条件是在第一个循环终止的情况下,此时若a中元素还有剩余则进行第二个循环,若b中元素还有剩余则进行第三个循环。
通过归并进行排序
归并排序的思想就是将要进行排序的数组分为两部分,通过merge方法将两个数组归并成一个有序数组。但是要怎么将两部分都变为有序的呢?那么就要对这两部分分别通过归并的方法进行排序。即将这两部分分别再进行一分为二,通过merge方法对其进行归并为有序的,而又要怎么保证这两部分的二分之一也是有序的呢,就要以此类推,直到到一个可终止的的条件为止,即每一个数组只有一个数据项。每一次都调用自身的归并方法对其两部分进行归并,这就是递归。
描述的或许没有图能够表达的清楚,下面就来看看以下的例子:
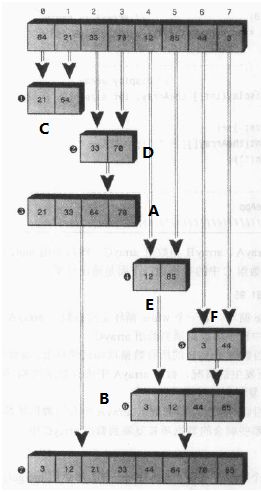
将数组中的数据四四分进行归并,但是前提是图中的AB必须有序,所以,需要先对AB进行归并排序,所以,在将A和B分别进行两两分,分别分成CD和EF,但同样的CD和EF也必须要有序,所以先对CD和EF进行归并排序,将其分别进行一一分,此时一个数据项没有什么有序可言,所以在数组的下半区,位置0-0和1-1的位置归并到0-1(即有序的C),2-2和3-3的位置被归并为2-3(即有序的D),类似的0-1和2-3被最终归并为0-3(即有序的A)。在数组的上半区,位置4-4和5-5的位置归并到4-5(即有序的E),位置6-6和7-7被归并到6-7(即有序的F),然后再将4-5和6-7归并为4-7,最后将0-3和4-7归并为0-7。此时就将原数组变为有序的了。
当数组的大小不是2的乘方时,就不能等分,此时就要对不同大小的两个数组进行归并,如下图过程:
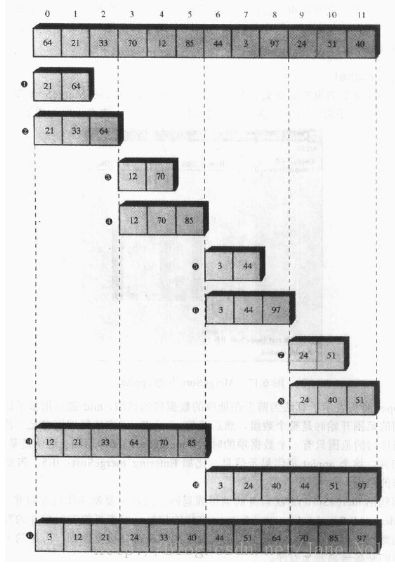
归并的Java代码
在数组类中分装相应的归并方法对数组的数据项进行排序。
class Array {
private int[] theArray;
private int nItem;
public Array(int max) {
theArray = new int[max];
nItem = 0;
}
public void insert(int value) {
theArray[nItem ++] = value;
}
public void displayList() {
for(int i = 0; i < nItem; i ++) {
System.out.print(thaArray[i] + " ");
}
System.out.println("");
}
public void mergeSort() {
int[] workspace = new int[nItem];
recMergeSort(workspace, 0, nItem-1);
}//end mergeSort
private void recMergeSort(int[] workspace, int lower, int upper) {
if(lower == upper)
return;
else {
mid = (lower + upper)/2;
recMergeSort(workspace, lower, mid);
recMergeSort(workspace, mid+1, upper);
merge(workspace, lower, mid+1, upper);
}
}//end recMergeSort
private void merge(int[] workspace, int lowPtr, int midPtr, int upper) {
int lower = lowPtr;
int mid = midPtr - 1;
int n = upper - lowPtr + 1; //进行排序的数据项个数
int j = 0;
while(lowPtr <= mid && midPtr <= upper)
if(theArray[lowPtr] < theArray[midPtr])
workspace[j ++] = theArray[lowPtr ++];
else
workspace[j ++] = theArray[midPtr ++];
while(lowPtr <= mid)
workspace[j ++] = theArray[lowPtr ++];
while(midPtr <= upper)
workspace[j ++] = theArray[midPtr ++];
for(j = 0; j < n; j ++)
theArray[lower + j] = workspace[j];
}//end merge
}//end Array
public MergeSortApp {
public static void main(String[] args) {
Array myArray = new Array(10);
myArray.insert(80);
myArray.insert(38);
myArray.insery(49);
myArray.insert(25);
myArray.insert(3);
myArray.insert(75);
myArray.displayList();
myArray.mergeSort();
myArray.displayList();
}
}控制台输出:
80 38 49 25 3 75
3 25 38 49 75 80
归并排序的效率
在最初我们已经讲到归并排序的时间为O(N*log(N)),那么这是怎么算出来的呢。我们假设排序的复制和比较是很耗时的,并且递归相关的操作不增加额外的开销。我们先来理解一下归并排序所需复制和比较的次数。
复制次数
在之前的例子中,当数据个数为8时,需要进行3层步骤,每一层都要进行8个数据的复制,所以总共要进行的复制次数为8×log2(8) = 8×3 = 24次复制。不过实际上,数据不仅会被复制到workspace当中,也会被复制到原数组当中,如上述Java程序的merge方法的最后一个步骤
for(j = 0; j < n; j ++)
theArray[lower + j] = workspace[j];这样的话复制的次数就增加了一倍,也就是说8个数据,要进行48次复制。
比较次数
对于归并排序,排序的比较次数总是要比复制少一些。当需要排序的数据个数为2的乘方时,数据最多要进行比较的次数总是比数据个数少一,最少要进行的比较次数为数据个数的一半。如下图:
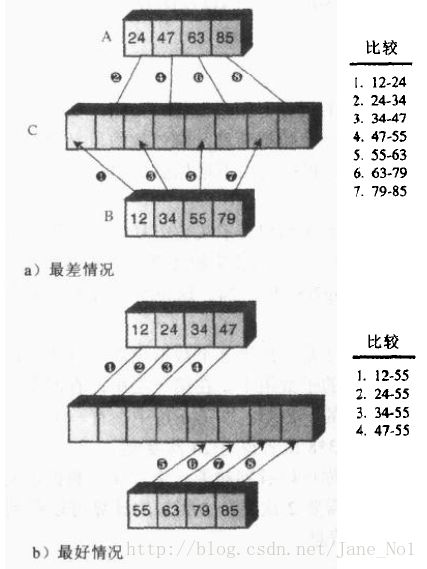
最差的情况是所有数据项大小都交织排列,所以这个时候8个数据要进行7次比较。当一个数组中的数据都比另一组的数据小时,此时就只需要进行4次比较为数据项个数的一半。
对每一次排序都要进行多次归并,将每次归并要进行比较的次数加起来就是总的比较次数,如下表:
| 步骤 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 总计 |
|---|---|---|---|---|---|---|---|---|
| 个数 | 2 | 2 | 4 | 2 | 2 | 4 | 8 | |
| 最多 | 1 | 1 | 3 | 1 | 1 | 3 | 7 | 17 |
| 最少 | 1 | 1 | 2 | 1 | 1 | 2 | 4 | 12 |