网络流24题20. 深海机器人问题

深海机器人问题

Description

深海资源考察探险队的潜艇将到达深海的海底进行科学考察。潜艇内有多个深海机器人。潜艇到达深海海底后，深海机器人将离开潜艇向预定目标移动。深海机器人在移动中还必须沿途采集海底生物标本。沿途生物标本由最先遇到它的深海机器人完成采集。每条预定路径上的生物标本的价值是已知的，而且生物标本只能被采集一次。本题限定深海机器人只能从其出发位置沿着向北或向东的方向移动，而且多个深海机器人可以在同一时间占据同一位置。
用一个 P×Q 网格表示深海机器人的可移动位置。西南角的坐标为（0,0），东北角的坐标为 (Q,P)。

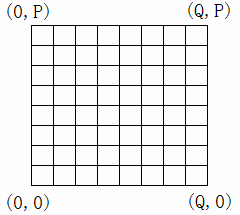
给定每个深海机器人的出发位置和目标位置，以及每条网格边上生物标本的价值。计算深海机器人的最优移动方案，使深海机器人到达目的地后，采集到的生物标本的总价值最高。

Input

第 1 行为深海机器人的出发位置数 a，和目的地数 b，第 2 行为 P 和 Q 的值。接下来的 P+1 行，每行有 Q 个正整数，表示向东移动路径上生物标本的价值，行数据依从南到北方向排列。再接下来的 Q+1 行，每行有 P 个正整数，表示向北移动路径上生物标本的价值，行数据依从西到东方向排列。接下来的 a 行，每行有 3 个正整数 k,x,y，表示有 k 个深海机器人从(x,y)位置坐标出发。再接下来的 b 行，每行有 3 个正整数 r,x,y，表示有 r 个深海机器人可选择(x,y)位置坐标作为目的地。

Output

输出采集到的生物标本的最高总价值。

Input

1 1
2 2
1 2
3 4
5 6
7 2
8 10
9 3
2 0 0
2 2 2

Output

42

题解

增加附加源S和附加汇T。
建图：
1.S向每个出发点连一条容量为该点出发机器人数，费用为0的边。
2.每个目的点向T连一条容量为该点终止机器人数，费用为0的边。
3.每点向东、北的相邻点连一条容量为1，费用为价值的边。
4.每点向东、北的相邻点连一条容量为inf，费用为0的边。
最大费用最大流就是答案。

#include
#include
#include
#include
using namespace std;
const int N = 1000 + 10, M = 1000000 + 10, inf = 0x3f3f3f3f;
struct Edge{
    int fr, to, cap, flow, cost;
}edg[M];
int nxt[M], hd[N], tot;
int n, m;
int s, t;
int q[N], inq[N], p[N], a[N], d[N];
int r, c;
void insert(int u, int v, int w, int x){
    edg[tot].fr = u, edg[tot].to = v, edg[tot].cap = w, edg[tot].flow = 0, edg[tot].cost = x;
    nxt[tot] = hd[u]; hd[u] = tot;
    tot++;
    edg[tot].fr = v, edg[tot].to = u, edg[tot].cap = 0, edg[tot].flow = 0, edg[tot].cost = -x;
    nxt[tot] = hd[v]; hd[v] = tot;
    tot++;
}
bool spfa(int &fl, int &cst){
    for(int i = s; i <= t; i++) d[i] = -inf;
    d[s] = 0; p[s] = 0; a[s] = inf;
    int head = 0, tail = 1;
    q[0] = s; inq[s] = 1;
    while(head != tail){
        int u = q[head++]; if(head == 1001) head = 0;
        inq[u] = 0;
        for(int i = hd[u]; i >= 0; i = nxt[i]){
            Edge &e = edg[i];
            if(d[e.to] < d[u] + e.cost && e.cap > e.flow){
                d[e.to] = d[u] + e.cost;
                p[e.to] = i;
                a[e.to] = min(a[u], e.cap - e.flow);
                if(!inq[e.to]){
                    q[tail++] = e.to; if(tail == 1001) tail = 0;
                    inq[e.to] = 1;
                }
            }
        }
    }
    if(d[t] == -inf) return false;
    fl += a[t];
    cst += a[t] * d[t];
    int u = t;
    while(u != s){
        edg[p[u]].flow += a[t];
        edg[p[u]^1].flow -= a[t];
        u = edg[p[u]].fr;
    }
    return true;
}
int get(int x, int y){
    return x * (m + 1) + y + 1;
}
void init(){
    scanf("%d%d%d%d", &r, &c, &n, &m);
    memset(hd, -1, sizeof(hd));
    int w;
    s = 0, t = get(n, m) + 1;
    for(int i = 0; i <= n; i++)
    for(int j = 0; j < m; j++){
        scanf("%d", &w);
        insert(get(i, j), get(i, j + 1), 1, w);
        insert(get(i, j), get(i, j + 1), inf, 0);
    }
    for(int j = 0; j <= m; j++)
    for(int i = 0; i < n; i++){
        scanf("%d", &w);
        insert(get(i, j), get(i + 1, j), 1, w);
        insert(get(i, j), get(i + 1, j), inf, 0);
    }
    int x, y;
    for(int i = 1; i <= r; i++){
        scanf("%d%d%d", &w, &x, &y);
        insert(s, get(x, y), w, 0);
    }
    for(int i = 1; i <= c; i++){
        scanf("%d%d%d", &w, &x, &y);
        insert(get(x, y), t, w, 0);
    }
}
void work(){
    int flow = 0, cost = 0;
    while(spfa(flow, cost));
    printf("%d\n", cost);
}
int main(){
    freopen("prog820.in", "r", stdin);
    freopen("prog820.out", "w", stdout);
    init();
    work();
    return 0;
}