基于numpy和python的反向传播算法的实现与分析

前言

本文基于反向传播算法的原理，实现了一个基于numpy和python的三层全连接神经网络，用于分类任务。其中在实现过程中，将会用代码的形式呈现梯度消失的现象，本文中的符号请参考我的前文《反向传播算法的公式推导》，代码将由github托管，有帮助的朋友欢迎star。
如有谬误，请联系指正。转载请注明出处。
联系方式：
e-mail: [email protected]
QQ: 973926198
github: https://github.com/FesianXu
完整代码开源： click me || 其中的sigmoid_base_BP.py

---

反向传播算法和神经网络

　　反向传播算法是用于神经网络反向传播误差和更新参数的，公式推导请参考我的博文《反向传播算法的公式推导》，其中的激活函数可以选择很多种，详情请参考我的博文《深度学习中激活函数的选择》。在大部分深度学习架构，如TensorFlow中，都对用户透明实现了BP算法，而我们并不需要详细了解BP算法的细节，只需要指定优化函数即可。这样不利于掌握BP算法和理解梯度消失，这里我们利用python和numpy实现了一个简单的BP算法模型，并且用此理解梯度消失
接下来简单说明下这个例子中的数据集和网络结构。

数据集

　　数据集由MATLAB生成，是一个人工数据集，生成代码如：

num = 100;
c1 = SphereGenerate([1,1,1], num, 1);
c2 = SphereGenerate([-1,2,-7], num, 0);
samples = [c1;c2];
save samples

数据格式为：

每一行是一个样本，前三维为feature维，最后一维为label，label用0和1表示，一共有2*num个样本。

绘制出来如：

网络结构

　　我们用一个简单的二层网络（只有一个隐藏层，一个输入层和一个输出层）即可拟合这个数据集，但是为了更好地观察到梯度消失，我们采用三层网络（两个隐藏层，一个输入层一个输出层）进行拟合，并且不考虑过拟合现象，目的只是为了拟合而已，这里需要注意。网络结构示意图如：
　　

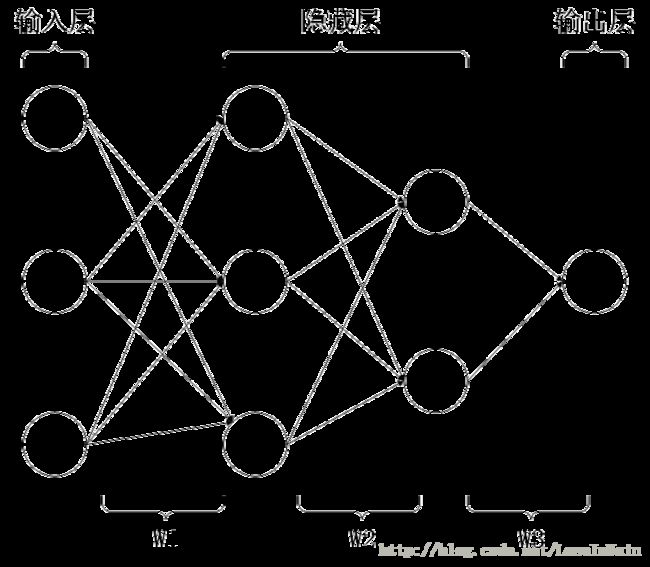
激活函数采用sigmoid函数，损失函数采用MSE函数，其公式表达如：
w l jk   是l-1层的第k个神经元与l层的第j个神经元的连接权值

b l j   是l-1层的第j个神经元的偏置。

z l j   是l层的第j神经元的输入。

a l j   是l层的第j神经元的激活输出。
用公式表达既是：

z l j =∑ k (w l jk ∗a l−1 k +b l j ) 

a l j =σ(z l j )=σ(∑ k (w l jk ∗a l−1 k +b l j )) 

其中的 σ(x)  为激活函数。多采用sigmoid，ReLU，tanh等。

C=12n ∗∑ x ||y−a L || 2   代价函数，其中L是神经网络的层数。
参数更新公式为：

w l jk :=w l jk −η∗∂C∂w l jk   

这里我们需要在迭代中求出的是 ∂C∂w l jk    , So now Let’s begin!

算法实现

数据处理

　　这里实现分离数据的feature和label，并且随机采样，用于喂养(feed)网络，代码很简单，如：

import scipy.io as sio
import numpy as np
import random

path = u'./samples.mat'
dataset = sio.loadmat(path)
mat = dataset['samples']

def random_get_data(mat, batch_size):
    batch_id = random.sample(range(mat.shape[0]), batch_size)
    ret_batch = mat[batch_id, 0:3]
    ret_label = mat[batch_id, 3:4]
    return ret_batch, ret_label

这样处理过后就可以开始建网络了。

网络参数初始化

n_input = 3
W1_hidden = 3
W2_hidden = 2
n_output = 1
batch_size = 128  # 每个batch大小

weights = {
    'W1': np.random.normal(size=(n_input, W1_hidden)),
    'W2': np.random.normal(size=(W1_hidden, W2_hidden)),
    'output': np.random.normal(size=(W2_hidden, n_output))
}

biases = {
    'B1': np.random.normal(size=(W1_hidden)),
    'B2': np.random.normal(size=(W2_hidden)),
    'output': np.random.normal(size=(n_output))
}

这里初始化网络参数，需要注意的就是参数都需要随机初始化，如果全部置为0，将会出现Dead Nerual的现象。

激活函数定义

def sigmoid(mat):
    return 1/(1+np.exp(-mat))

def d_sigmoid(mat):
    m = sigmoid(mat)
    return m*(1-m)

这里定义了sigmoid函数 σ(x)  和其导数 σ ′ (x) 

网络前向传播

def forward(batch):
    h1 = np.dot(batch, weights['W1'])+biases['B1']
    h1 = sigmoid(h1)
    h2 = np.dot(h1, weights['W2'])+biases['B2']
    h2 = sigmoid(h2)
    output = np.dot(h2, weights['output'])+biases['output']
    ret = sigmoid(output)
    return ret

def forward_1(x_input):
    z1 = np.dot(x_input, weights['W1'])+biases['B1']
    a1 = sigmoid(z1)
    return z1, a1

def forward_2(x_input):
    z2 = np.dot(x_input, weights['W2'])+biases['B2']
    a2 = sigmoid(z2)
    return z2, a2

def forward_3(x_input):
    z3 = np.dot(x_input, weights['output'])+biases['output']
    a3 = sigmoid(z3)
    return z3, a3

其中forward指的是全网络前向，而forward_x指的是前向至某一层，观察代码可以很好看出来。需要注意的是，numpy的dot才是我们线性代数中定义的矩阵乘法，用matmul或者直接“*”是会出错的哦。

计算梯度（反向传播误差）

梯度表示为：

δ 3 =[δ 3 1 ] 

δ 2 =[δ 2 1 ,δ 2 2 ] 

δ 1 =[δ 1 1 ,δ 1 2 ,δ 1 3 ] 

这里的计算梯度，即是反向传播误差，是这个算法中的核心，具体的计算公式参见我的博文《反向传播算法的公式推导》，这里直接给出代码：

def cal_gradient(batch, label):
    z1, a1 = forward_1(batch)
    z2, a2 = forward_2(a1)
    z3, a3 = forward_3(a2)
    sig31 = np.sum((a3-label)*d_sigmoid(z3))/batch_size

    sig21 = sig31*weights['output'][0, 0]*np.sum(d_sigmoid(z2[:, 0]))/batch_size
    sig22 = sig31*weights['output'][1, 0]*np.sum(d_sigmoid(z2[:, 1]))/batch_size

    sig11 = np.sum(d_sigmoid(z1[:, 0]))*(sig21*weights['W2'][0, 0]+sig22*weights['W2'][0, 1])/batch_size
    sig12 = np.sum(d_sigmoid(z1[:, 1]))*(sig21*weights['W2'][1, 0]+sig22*weights['W2'][1, 1])/batch_size
    sig13 = np.sum(d_sigmoid(z1[:, 2]))*(sig21*weights['W2'][2, 0]+sig22*weights['W2'][2, 1])/batch_size

    sig1 = np.array([sig11, sig12, sig13])
    sig2 = np.array([sig21, sig22])
    sig3 = np.array([sig31])
    return sig3, sig2, sig1

如果我们选择一个batch给这个反向传播网络，我们会发现sig3比sig2大一个数量级，而sig2比sig1大一个数量级，sig1会变得非常小，如：

sig1 : [  1.53353099e-05   2.37135061e-06  -7.50600600e-05]
sig2 : [ -2.62139732e-04  -6.41999616e-05]
sig3 : [ 0.00145859]

原因我们以前提到过，很简单，是因为sigmoid函数的导数在输入过大或者过小时输出非常小，在经过多层之后，其乘积自然就变得非常小了。这样就称为梯度消失。

更新参数

learning_rate = 0.1
def update(batch, sig1, sig2, sig3):
    z1, a1 = forward_1(batch)
    z2, a2 = forward_2(a1)
    z3, a3 = forward_3(a2)
    a1 = np.sum(a1, axis=0)/batch_size
    a2 = np.sum(a2, axis=0)/batch_size
    a3 = np.sum(a3, axis=0)/batch_size
    a1 = np.reshape(a1, (a1.shape[0], 1))
    a2 = np.reshape(a2, (a2.shape[0], 1))
    a3 = np.reshape(a3, (a3.shape[0], 1))
    sig2 = np.reshape(sig2, (sig2.shape[0], 1))
    sig1 = np.reshape(sig1, (sig1.shape[0], 1))
    sig3 = np.reshape(sig3, (sig3.shape[0], 1))

    input = np.sum(batch, axis=0)/batch_size
    weights['W1'] = weights['W1']-learning_rate*(input*np.transpose(sig1))
    weights['W2'] = weights['W2']-learning_rate*(a1*np.transpose(sig2))
    weights['output'] = weights['output']-learning_rate*(a2*np.transpose(sig3))
    biases['B1'] = biases['B1']-learning_rate*np.transpose(sig1)
    biases['B2'] = biases['B2']-learning_rate*np.transpose(sig2)
    biases['output'] = biases['output']-learning_rate*np.transpose(sig3)

这里就是实现公式：

w l jk :=w l jk −η∗∂C∂w l jk   

训练过程

sum = 0
i = 0
import time
begin = time.clock()
while True:
    batch, label = random_get_data(mat, batch_size)
    sig3, sig2, sig1 = cal_gradient(batch, label)
    update(batch, sig1, sig2, sig3)
    loss = cal_loss(batch, label)
    sum += loss
    i += 1
    if i % 1000 == 0:
        loss = sum/1000
        sum = 0
        print(loss)
        if loss < 0.01:
            break
end = time.clock()
print('cost time = %f s' % (end-begin))

我们可以观察到loss在不断减小如：

0.118453573991
0.118059621824
0.117681894633
0.117301278874
0.116869727509
0.116405024212
`
`
`
0.0277541827357
0.027673502213
0.02756174451
0.0274564410939
0.02735896855
0.027277260658
`
`
`
0.0101743793372
0.0101526569715
0.0101361149521
0.0101083053208
0.0100893087706
0.0100683488091
0.0100510519172
0.0100343181771
0.0100149190862
0.00999414208507

最后耗时：1037.160441 s 可见其更新速度是非常慢的，其一大部分的原因就是梯度消失，如果将激活函数换成ReLU函数，这个问题将会得到很大的改善。

更改激活函数

　　之前使用的激活函数是sigmoid函数，在使用过程中，我们发现sigmoid缺点挺多，比如容易造成梯度消失，计算较为复杂等，因此学者们提出了ReLU激活函数，其计算极为简单，而且不会出现梯度消失的问题：

ReLU=max(x,0) 

在程序中添加ReLU函数和其导数d_relu:

def relu(mat):
    return np.maximum(mat, 0)

def d_relu(mat):
    return 1.0*(mat > 0)

并且将模型中的中间两层的网络激活函数改为relu，输出层仍然为sigmoid，以提供更大的非线性性。
最后耗时为：309.193749 s，可见明显快于sigmoid函数的收敛速度。

小问题，待解决

　　在程序中，采用的是随机批量梯度下降法（BSGD），每一个batch大小为batch_size，在更新参数的过程中，将会涉及到输入值 x l   和激活值 a l i   ，由于存在多个样本，这里的输入值和激活值均采用的是一个batch内的均值，不知在标准的BP算法中是不是这样实现的，实验结果是可以收敛，就是不知道会不会影响收敛速度和泛化能力。