ELMo解读(论文 + PyTorch源码)
ELMo的概念也是很早就出了,应该是18年初的事情了。但我仍然是后知后觉,居然还是等BERT出来很久之后,才知道有这么个东西。这两天才仔细看了下论文和源码,在这里做一些记录,如果有不详实的地方,欢迎指出~
文章目录
- 前言
- 一. ELMo原理
- 1. ELMo整体模型结构
- 2. 字符编码层
- 3. biLMs原理
- 4. 生成ELMo词向量
- 5. 结合下游NLP任务
- 二. PyTorch实现
- 1. 字符编码层
- 2. biLMs层
- 3. 生成ELMo词向量
- 三. 实验
- 四. 一些分析
- 1. 使用哪些层的输出?
- 2. 在哪里加入ELMo?
- 3. 每层输出的侧重点是什么?
- 4. 效率分析
- 五. 总结
- 传送门
前言
ELMo出自Allen研究所在NAACL2018会议上发表的一篇论文《Deep contextualized word representations》,从论文名称看,应该是提出了一个新的词表征的方法。据他们自己的介绍:ELMo是一个深度带上下文的词表征模型,能同时建模(1)单词使用的复杂特征(例如,语法和语义);(2)这些特征在上下文中会有何变化(如歧义等)。这些词向量从深度双向语言模型(biLM)的隐层状态中衍生出来,biLM是在大规模的语料上面Pretrain的。它们可以灵活轻松地加入到现有的模型中,并且能在很多NLP任务中显著提升现有的表现,比如问答、文本蕴含和情感分析等。听起来非常的exciting,它的原理也十分reasonable!下面就将针对论文及其PyTorch源码进行剖析,具体的资料参见文末的传送门。
这里先声明一点:笔者认为“ELMo”这个名称既可以代表得到词向量的模型,也可以是得出的词向量本身,就像Word2Vec、GloVe这些名称一样,都是可以代表两个含义的。下面提到ELMo时,一般带有“模型”相关字眼的就是指的训练出词向量的模型,而带有“词向量”相关字眼的就是指的得出的词向量。
一. ELMo原理
之前我们一般比较常用的词嵌入的方法是诸如Word2Vec和GloVe这种,但这些词嵌入的训练方式一般都是上下文无关的,并且对于同一个词,不管它处于什么样的语境,它的词向量都是一样的,这样对于那些有歧义的词非常不友好。因此,论文就考虑到了要根据输入的句子作为上下文,来具体计算每个词的表征,提出了ELMo(Embeddings from Language Model)。它的基本思想,用大白话来说就是,还是用训练语言模型的套路,然后把语言模型中间隐含层的输出提取出来,作为这个词在当前上下文情境下的表征,简单但很有用!
1. ELMo整体模型结构
对于ELMo的模型结构,其实论文中并没有给出具体的图(这点对于笔者这种想象力极差的人来说很痛苦),笔者通过整合论文里面的蛛丝马迹以及PyTorch的源码,得出它大概是下面这么个东西(手残党画的丑,勿怪):
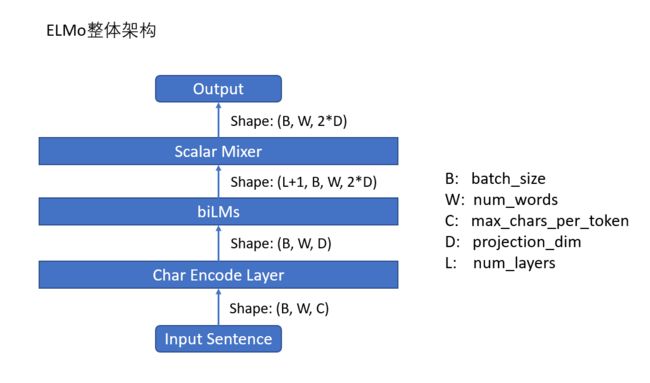
假设输入的句子维度为 B ∗ W ∗ C B * W * C B∗W∗C,这里的 B B B 表示batch_size, W W W 表示num_words,即一句话中的单词数目,在一个batch中可能需要padding, C C C 表示max_characters_per_token,即每个单词的字符数目,这里论文里面用了固定值50,不根据每个batch的不同而动态设置, D D D 表示projection_dim,即单词输入biLMs的embedding_size,或者理解为最终生成的ELMo词向量维度的 1 / 2 1 / 2 1/2。
从图里面看,输入的句子会经过:
- Char Encode Layer: 即首先经过一个字符编码层,因为ELMo实际上是基于char的,所以它会先对每个单词中的所有char进行编码,从而得到这个单词的表示。因此经过字符编码层出来之后的维度为 B ∗ W ∗ D B * W * D B∗W∗D,这就是我们熟知的对于一个句子在单词级别上的编码维度。
- biLMs:随后该句子表示会经过biLMs,即双向语言模型的建模,内部其实是分开训练了两个正向和反向的语言模型,而后将其表征进行拼接,最终得到的输出维度为 ( L + 1 ) ∗ B ∗ W ∗ 2 D (L+1) * B * W * 2D (L+1)∗B∗W∗2D,+1实际上是加上了最初的embedding层,有点儿像residual,后面在“biLMs”部分会详细提到。
- Scalar Mixer:紧接着,得到了biLMs各个层的表征之后,会经过一个混合层,它会将前面这些层的表示进行线性融合(后面在“生成ELMo词向量”部分会进行详细说明),得出最终的ELMo向量,维度为 B ∗ W ∗ 2 D B * W * 2D B∗W∗2D。
这里只是对ELMo模型从全局上进行的一个统观,对每个模块里面的结构还是很懵逼?没关系,下面我们逐一来进行剖析:
2. 字符编码层
这一层即“Char Encode Layer”,它的输入维度是 B ∗ W ∗ C B * W * C B∗W∗C,输出维度是 B ∗ W ∗ D B * W * D B∗W∗D,经查看源码,它的结构图长这样:

画的有点儿乱,大家将就着看~
首先,输入的句子会被reshape成 B W ∗ C BW * C BW∗C,因其是针对所有的char进行处理。然后会分别经过如下几个层:
- Char Embedding:这就是正常的embedding层,针对每个char进行编码,实际上所有char的词表大概是262,其中0-255是char的unicode编码,256-261这6个分别是
- Multi-Scale卷积层:这里用的是不同scale的卷积层,注意是在宽度上扩展,而不是深度上,即输入都是一样的,卷积之间的不同在于其
kernel_size和channel_size的大小不同,用于捕捉不同n-grams之间的信息,这点其实是仿照 TextCNN 的模型结构。假设有 m m m个这样的卷积层,其kernel_size从 k 1 , k 2 , . . . , k m k1, k2, ..., km k1,k2,...,km,比如1,2,3,4,5,6,7这种,其channel_size从 d 1 , d 2 , . . . , d m d1, d2, ..., dm d1,d2,...,dm,比如32,64,128,256,512,1024这种。注意:这里的卷积都是1维卷积,即只在序列长度上做卷积。与图像中的处理类似,在卷积之后,会经过MaxPooling进行池化,这里的目的主要在于经过前面卷积出的序列长度往往不一致,后期没办法进行合并,所以这里在序列维度上进行MaxPooling,其实就是取一个单词中最大的那个char的表示作为整个单词的表示。最后再经过激活层,这一步就算结束了。根据不同的channel_size的大小,这一步的输出维度分别为 B W ∗ d 1 , B W ∗ d 2 , . . . , B W ∗ d m BW * d1, BW * d2, ..., BW * dm BW∗d1,BW∗d2,...,BW∗dm。 - Concat层:上一步得出的是m个不同维度的矩阵,为了方便后期处理,这里将其在最后一维上进行拼接,而后将其reshape回单词级别的维度 B ∗ W ∗ ( d 1 + d 2 + . . . + d m ) B * W * (d1+d2+...+dm) B∗W∗(d1+d2+...+dm)。
- Highway层:Highway(参见:https://arxiv.org/abs/1505.00387 )是仿照图像中residual的做法,在NLP领域中常有应用,看代码里面的实现,这一层实现的公式见下面:其实就是一种全连接+残差的实现方式,只不过这里还需要一个element-wise的gate矩阵对 x x x和 f ( A ( x ) ) f(A(x)) f(A(x))进行变换。这里需要经过 H H H 层这样的Highway层,输出维度仍为 B ∗ W ∗ ( d 1 + d 2 + . . . + d m ) B * W * (d1+d2+...+dm) B∗W∗(d1+d2+...+dm)。
y = g ∗ x + ( 1 − g ) ∗ f ( A ( x ) ) , g = S i g m o i d ( B ( x ) ) y = g * x + (1 - g) * f(A(x)), g = Sigmoid(B(x)) y=g∗x+(1−g)∗f(A(x)),g=Sigmoid(B(x))
- Linear映射层:经过前面的计算,得到的向量维度 d 1 + d 2 + . . . + d m d1+d2+...+dm d1+d2+...+dm往往比较长,这里额外加了一层的Linear进行映射,将维度映射到 D D D,作为词的embedding送入后续的层中,这里输出的维度为 B ∗ W ∗ D B * W * D B∗W∗D。
3. biLMs原理
ELMo主要是建立在biLMs(双向语言模型)上的,下面先从数学上介绍一下什么是biLMs。
具体来说,给定一个有 N N N个token的序列 ( t 1 , t 2 , . . . , t N ) (t_1, t_2, ..., t_N) (t1,t2,...,tN),前向的语言模型(一般是多层的LSTM之类的)用于计算给定前面tokens的情况下当前token的概率,即:
p ( t 1 , t 2 , . . . , t N ) = ∏ k = 1 N p ( t k ∣ t 1 , t 2 , . . . , t k − 1 ) p(t_1, t_2, ..., t_N) = \prod_{k=1}^{N} p(t_k | t_1, t_2, ..., t_{k-1}) p(t1,t2,...,tN)=k=1∏Np(tk∣t1,t2,...,tk−1)
在每一个位置 k k k,模型都会在每一层输出一个上下文相关的表征 h → k , j L M \overrightarrow{h}_{k, j}^{LM} hk,jLM,这里的 j = 1 , . . . , L j = 1, ..., L j=1,...,L表示第几层。顶层的输出 h → k , L L M \overrightarrow{h}_{k, L}^{LM} hk,LLM用于预测下一个token: t k + 1 t_{k+1} tk+1。
同样地,反向的语言模型训练与正向的一样,只不过输入是反过来的,即计算给定后面tokens的情况下当前token的概率:
p ( t 1 , t 2 , . . . , t N ) = ∏ k = 1 N p ( t k ∣ t k + 1 , t k + 2 , . . . , t N ) p(t_1, t_2, ..., t_N) = \prod_{k=1}^{N} p(t_k | t_{k+1}, t_{k+2}, ..., t_N) p(t1,t2,...,tN)=k=1∏Np(tk∣tk+1,tk+2,...,tN)
同样,反向的LM在每个位置 k k k,也会在每一层生成一个上下文相关的表征 h ← k , j L M \overleftarrow{h}_{k, j}^{LM} hk,jLM。
ELMo用的biLMs就是同时结合正向和反向的语言模型,其目标是最大化如下的似然值:
∑ k = 1 N ( log p ( t k ∣ t 1 , . . . , t k − 1 ; Θ x , Θ → L S T M , Θ s ) + ( log p ( t k ∣ t k + 1 , . . . , t N ; Θ x , Θ ← L S T M , Θ s ) ) \sum_{k=1}^N(\log p(t_k | t_1, ..., t_{k-1}; \Theta_x, \overrightarrow \Theta _{LSTM}, \Theta_s) + (\log p(t_k | t_{k+1}, ..., t_N; \Theta_x, \overleftarrow \Theta _{LSTM}, \Theta_s)) k=1∑N(logp(tk∣t1,...,tk−1;Θx,ΘLSTM,Θs)+(logp(tk∣tk+1,...,tN;Θx,ΘLSTM,Θs))
里面的 Θ x \Theta_x Θx、 Θ s \Theta_s Θs和 Θ → L S T M \overrightarrow \Theta _{LSTM} ΘLSTM及 Θ ← L S T M \overleftarrow \Theta _{LSTM} ΘLSTM分别是词嵌入,输出层(Softmax之前的)以及正反向LSTM的参数。
可以看出,其实就是相当于分别训练了正向和反向的两个LM。 好像也只能分开进行训练,因为LM不能训练双向的。
示意图的话,就是下面这种多层BiLSTM的样子:
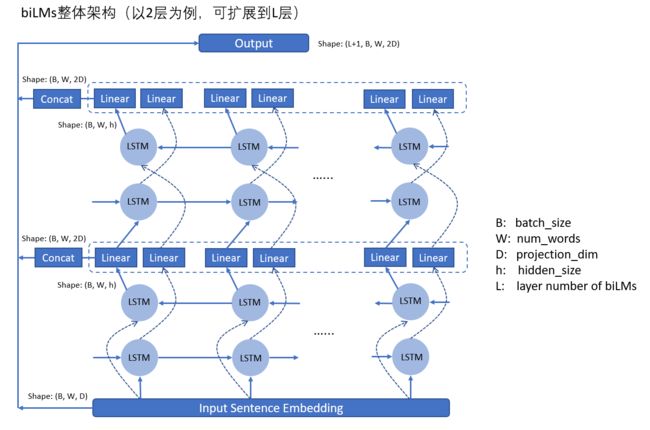
这里的 h h h 表示LSTM单元的hidden_size,可能会比较大,比如 D = 512 , h = 4096 D = 512, h = 4096 D=512,h=4096这样。所以在每一层结束后还需要一个Linear层将维度从 h h h 映射为 D D D,而后再输入到下一层中。最后的输出是将每一层的所有输出以及embedding的输出,进行stack,每一层的输出里面又是对每个timestep的正向和反向的输出进行concat,因而最后的输出维度为 ( L + 1 ) ∗ B ∗ W ∗ 2 D (L+1) * B * W * 2D (L+1)∗B∗W∗2D,这里的 L + 1 L + 1 L+1 中的 + 1 +1 +1 就代表着那一层embedding输出,其会复制成两份,以与biLMs每层的输出维度保持一致。
4. 生成ELMo词向量
在经过了biLMs层之后,得到的表征维度为 ( L + 1 ) ∗ B ∗ W ∗ 2 D (L+1) * B * W * 2D (L+1)∗B∗W∗2D,接下来就需要生成最终的ELMo向量了!
对于每一个token t k t_k tk, L L L 层的biLMs,生成出来的表征有 2 L + 1 2L + 1 2L+1 个,如下公式:
R k = { x k L M , h → k , j L M , h ← k , j L M ∣ j = 1 , . . . , L } = { h k , j L M ∣ j = 0 , . . , L } R_k = \{x_k^{LM}, \overrightarrow{h}_{k,j}^{LM}, \overleftarrow{h}_{k,j}^{LM} | j = 1, ..., L\} = \{h_{k,j}^{LM} | j = 0, .., L\} Rk={xkLM,hk,jLM,hk,jLM∣j=1,...,L}={hk,jLM∣j=0,..,L}
这里的 h k , 0 L M h_{k,0}^{LM} hk,0LM是词的embedding输出, h k , j L M = [ h → k , j L M ; h ← k , j L M ] h_{k,j}^{LM} = [\overrightarrow{h}_{k,j}^{LM}; \overleftarrow{h}_{k,j}^{LM}] hk,jLM=[hk,jLM;hk,jLM]表示每一层的正向和反向输出拼接后的结果。
对于这些表征,论文用如下公式对它们做了一个scalar mixer:
E L M o k t a s k = E ( R k ; Θ t a s k ) = γ t a s k ∑ j = 0 L s j t a s k h k , j L M ELMo_{k}^{task} = E(R_k; \Theta^{task}) = \gamma^{task} \sum_{j=0}^L s_j^{task} h_{k,j}^{LM} ELMoktask=E(Rk;Θtask)=γtaskj=0∑Lsjtaskhk,jLM
这里的 s j t a s k s_j^{task} sjtask是一个softmax后的概率值,标量参数 γ t a s k \gamma^{task} γtask是用于对整个ELMo向量进行scale上的缩放。这两部分都是作为参数来学习的,针对不同任务会有不同的值。
同时论文里面还提到,每一层输出的分布之间可能会有较大差别,所以有时也会在线性融合之前,为每层的输出做一个Layer Normalization,这与Transformer里面一致。
经过Scalar Mixer之后的向量维度为 B ∗ W ∗ 2 D B * W * 2D B∗W∗2D,即为生成的ELMo词向量,可以用于后续的任务。
5. 结合下游NLP任务
一般ELMo模型会在一个超大的语料库上进行预训练,因为是训练语言模型,不需要任何的标签,纯文本就可以,因而这里可以用超大的语料库,这一点的优势是十分明显的。训练完ELMo模型之后,就可以输入一个新句子,得到其中每个单词在当前这个句子上下文下的ELMo词向量了。
论文中提到,在训练的时候,发现使用合适的dropout和L2在ELMo模型上时会提升效果。
此时这个词向量就可以接入到下游的NLP任务中,比如问答、情感分析等。从接入的位置来看,可以与下游NLP任务本身输入的embedding拼接在一起,也可以与其输出拼接在一起。而从模型是否固定来看,又可以将ELMo词向量预先全部提取出来,即固定ELMo模型不让其训练,也可以在训练下游NLP任务时顺带fine-tune这个ELMo模型。总之,使用起来非常的方便,可以插入到任何想插入的地方进行增补。
二. PyTorch实现
这里参考的主要是allennlp里面与ELMo本身有关的部分,涉及到biLMs的模型实现,以及ELMo推理部分,会只列出核心的部分,细枝末节的代码就不列举了。至于如何与下游的NLP任务结合以及fine-tune,还需要读者自己去探索和实践,这里不做说明!
1. 字符编码层
这里实现的就是前面提到的Char Encode Layer。
首先是multi-scale CNN的实现:
# multi-scale CNN
# 网络定义
for i, (width, num) in enumerate(filters):
conv = torch.nn.Conv1d(
in_channels=char_embed_dim,
out_channels=num,
kernel_size=width,
bias=True
)
self.add_module('char_conv_{}'.format(i), conv)
# forward函数
def forward(sef, character_embedding)
convs = []
for i in range(len(self._convolutions)):
conv = getattr(self, 'char_conv_{}'.format(i))
convolved = conv(character_embedding)
# (batch_size * sequence_length, n_filters for this width)
convolved, _ = torch.max(convolved, dim=-1)
convolved = activation(convolved)
convs.append(convolved)
# (batch_size * sequence_length, n_filters)
token_embedding = torch.cat(convs, dim=-1)
return token_embedding
然后是highway的实现:
# HighWay
# 网络定义
self._layers = torch.nn.ModuleList([torch.nn.Linear(input_dim, input_dim * 2)
for _ in range(num_layers)])
# forward函数
def forward(self, inputs):
current_input = inputs
for layer in self._layers:
projected_input = layer(current_input)
linear_part = current_input
# NOTE: if you modify this, think about whether you should modify the initialization
# above, too.
nonlinear_part, gate = projected_input.chunk(2, dim=-1)
nonlinear_part = self._activation(nonlinear_part)
gate = torch.sigmoid(gate)
current_input = gate * linear_part + (1 - gate) * nonlinear_part
return current_input
2. biLMs层
这部分实际上是两个不同方向的BiLSTM训练,然后输出经过映射后直接进行拼接即可,代码如下:(以单向单层的为例)
# 网络定义
# input_size:输入embedding的维度
# hidden_size:输入和输出hidden state的维度
# cell_size:LSTMCell的内部维度。
# 一般input_size = hidden_size = D, hidden_size即为h。
self.input_linearity = torch.nn.Linear(input_size, 4 * cell_size, bias=False)
self.state_linearity = torch.nn.Linear(hidden_size, 4 * cell_size, bias=True)
self.state_projection = torch.nn.Linear(cell_size, hidden_size, bias=False)
# forward函数
def forward(self, inputs, batch_lengths, initial_state):
for timestep in range(total_timesteps):
# Do the projections for all the gates all at once.
# Both have shape (batch_size, 4 * cell_size)
projected_input = self.input_linearity(timestep_input)
projected_state = self.state_linearity(previous_state)
# Main LSTM equations using relevant chunks of the big linear
# projections of the hidden state and inputs.
input_gate = torch.sigmoid(projected_input[:, (0 * self.cell_size):(1 * self.cell_size)] +
projected_state[:, (0 * self.cell_size):(1 * self.cell_size)])
forget_gate = torch.sigmoid(projected_input[:, (1 * self.cell_size):(2 * self.cell_size)] +
projected_state[:, (1 * self.cell_size):(2 * self.cell_size)])
memory_init = torch.tanh(projected_input[:, (2 * self.cell_size):(3 * self.cell_size)] +
projected_state[:, (2 * self.cell_size):(3 * self.cell_size)])
output_gate = torch.sigmoid(projected_input[:, (3 * self.cell_size):(4 * self.cell_size)] +
projected_state[:, (3 * self.cell_size):(4 * self.cell_size)])
memory = input_gate * memory_init + forget_gate * previous_memory
# shape (current_length_index, cell_size)
pre_projection_timestep_output = output_gate * torch.tanh(memory)
# shape (current_length_index, hidden_size)
timestep_output = self.state_projection(pre_projection_timestep_output)
output_accumulator[0:current_length_index + 1, index] = timestep_output
# Mimic the pytorch API by returning state in the following shape:
# (num_layers * num_directions, batch_size, ...). As this
# LSTM cell cannot be stacked, the first dimension here is just 1.
final_state = (full_batch_previous_state.unsqueeze(0),
full_batch_previous_memory.unsqueeze(0))
return output_accumulator, final_state
3. 生成ELMo词向量
这部分即为Scalar Mixer,其代码如下:
# 参数定义
self.scalar_parameters = ParameterList(
[Parameter(torch.FloatTensor([initial_scalar_parameters[i]]),
requires_grad=trainable) for i
in range(mixture_size)])
self.gamma = Parameter(torch.FloatTensor([1.0]), requires_grad=trainable)
# forward函数
def forward(tensors, mask):
def _do_layer_norm(tensor, broadcast_mask, num_elements_not_masked):
tensor_masked = tensor * broadcast_mask
mean = torch.sum(tensor_masked) / num_elements_not_masked
variance = torch.sum(((tensor_masked - mean) * broadcast_mask)**2) / num_elements_not_masked
return (tensor - mean) / torch.sqrt(variance + 1E-12)
normed_weights = torch.nn.functional.softmax(torch.cat([parameter for parameter
in self.scalar_parameters]), dim=0)
normed_weights = torch.split(normed_weights, split_size_or_sections=1)
if not self.do_layer_norm:
pieces = []
for weight, tensor in zip(normed_weights, tensors):
pieces.append(weight * tensor)
return self.gamma * sum(pieces)
else:
mask_float = mask.float()
broadcast_mask = mask_float.unsqueeze(-1)
input_dim = tensors[0].size(-1)
num_elements_not_masked = torch.sum(mask_float) * input_dim
pieces = []
for weight, tensor in zip(normed_weights, tensors):
pieces.append(weight * _do_layer_norm(tensor,
broadcast_mask, num_elements_not_masked))
return self.gamma * sum(pieces)
三. 实验
这里主要列举一些在实际下游任务上结合ELMo的表现,分别是SQuAD(问答任务)、SNLI(文本蕴含)、SRL(语义角色标注)、Coref(共指消解)、NER(命名实体识别)以及SST-5(情感分析任务),其结果如下:
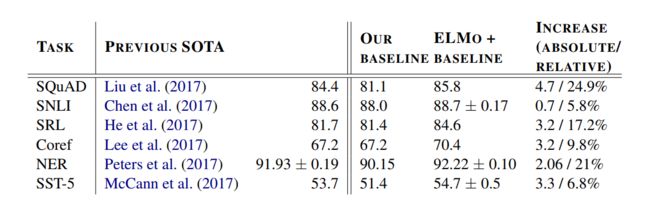
可见,基本都是在一个较低的baseline的情况下,用了ELMo后,达到了超越之前SoTA的效果!
四. 一些分析
论文中,作者也做了一些有趣的分析,从各个角度窥探ELMo的优势和特性。比如:
1. 使用哪些层的输出?
作者探索了使用不同biLMs层带来的效果,以及使用不同的L2范数的权重,如下表所示:

这里面的Last Only指的是只是用biLM最顶层的输出, λ \lambda λ 指的是L2范数的权重,可见使用所有层的效果普遍比较好,并且较低的L2范数效果也较好,因其让每一层的表示都趋于不同,当L2范数的权重较大时,会让模型所有层的参数值趋于一致,导致模型每层的输出也会趋于一致。
2. 在哪里加入ELMo?
前面提到过,可以在输入和输出的时候加入ELMo向量,作者比较了这两者的不同:

在问答和文本蕴含任务上,是同时在输入和输出加入ELMo的效果较好,而在语义角色标注任务上,则是只在输入加入比较好。论文猜测这个原因可能是因为,在前两个任务上,都需要用到attention,而在输出的时候加入ELMo,能让attention直接看到ELMo的输出,会对整个任务有利。而在语义角色标注上,与任务相关的上下文表征要比biLMs的通用输出更重要一些。
3. 每层输出的侧重点是什么?
论文通过实验得出,在biLMs的低层,表征更侧重于诸如词性等这种语法特征,而在高层的表征则更侧重于语义特征。比如下面的实验结果:

左边的任务是语义消歧,右边的任务是词性标注,可见在语义消歧任务上面,使用第二层的效果比第一层的要好;而在词性标注任务上面,使用第一层的效果反而比使用第二层的效果要好。
总体来看,还是使用所有层输出的效果会更好,具体的weight让模型自己去学就好了。
4. 效率分析
一般而言,用了预训练模型的网络往往收敛的会更快,同时也可以使用更少的数据集。论文通过实验验证了这一点:

比如在SRL任务中,使用了ELMo的模型仅使用1%的数据集就能达到不使用ELMo模型在使用10%数据集的效果!
五. 总结
ELMo具有如下的优良特性:
- 上下文相关:每个单词的表示取决于使用它的整个上下文。
- 深度:单词表示组合了深度预训练神经网络的所有层。
- 基于字符:ELMo表示纯粹基于字符,然后经过CharCNN之后再作为词的表示,解决了OOV问题,而且输入的词表也很小。
- 资源丰富:有完整的源码、预训练模型、参数以及详尽的调用方式和例子,又是一个造福伸手党的好项目!而且:还有人专门实现了多语的,好像是哈工大搞的,戳这里看项目。
传送门
论文:https://arxiv.org/pdf/1802.05365.pdf
项目首页:https://allennlp.org/elmo
源码:https://github.com/allenai/allennlp (PyTorch,关于ELMo的部分戳这里)
https://github.com/allenai/bilm-tf (TensorFlow)
多语言:https://github.com/HIT-SCIR/ELMoForManyLangs (哈工大CoNLL评测的多国语言ELMo,还有繁体中文的)