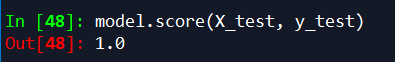2.【笔记】统计学习方法——sklearn之knn

参考文献：李航.统计学习方法[M].北京:清华大学出版社,2018.
该部分笔记全部总结自这本书。
KDT这部分代码我是参考自一个GitHub上面开源代码，找不到那个帖子了，再看到的时候再回来补超链接吧。

3.K近邻

3.1 距离公式

欧式距离、马氏距离、闵式距离、曼哈顿距离等。
距离公式在这里已经总结过了：距離公式大全！傳送門在這裏，點擊这里！

3.2 模型

3.2.1 原理

对于输入的测试集，每个实例点周围的近邻点的分类是确定的，根据所确定的k值，将K个近邻点组成一个单元（cell），在每个cell中，比例大的那部分点的属性决定该实例点的属性。

3.2.2 距离度量

$$L_p(x_i,x_j)=(\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}{|}^p{)}^{\frac{1}{p}}$$

下图给出了不同P的取值下，与原点$L_p$距离为1的点的集合：

（图片引用自：李航.统计学习方法，下不累述。）

3.2.3 K值得选择

• k过小：学习的近似误差会变小，但是估计误差变大，预测结果会对近邻的实例点非常敏感。如果近邻点是噪声点，则估计错误。
• 换言之，k减小，模型复杂，容易过拟合。
• 如果k=N，则无论实例是什么，都会预测成为训练集中实力最多的类，模型过于简单。
• 实际应用，交叉验证选取k。

3.2.4 分类决策规则

在每一个实例点的单元里，多数表决规则。相当于经验风险最小。推导请看教材。

3.3 k近邻的实现：kd树

k近邻的最简单实现方法是线性扫描：计算预测实例与每一个训练实例的距离。计算量大耗时。

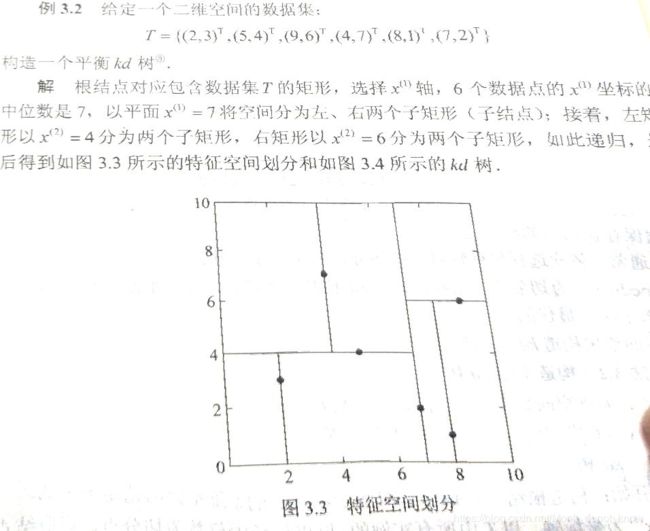
3.3.1 构造平衡kd树

• kd tree：是二叉树，对实例点进行存储以快速检索的树形数据结构。

• 构造kd树：用垂直于坐标轴的超平面将K维空间切分，构成一系列的K维超矩阵区域，每一个结点对应于一个k维超矩形区域

• （1）开始：构造根结点，根结点对应于包含T的k维空间的超矩形区域。选择$x^{(1)}$为坐标轴，以T中所有的实例的$x^{(1)}$坐标的中位数为切分点，将根结点对应的超矩形区域分为两个子区域。切分有通过切分点并与坐标轴$x^{1}$垂直的超平面实现

  • 由根结点生成深度为1左、右子节点：左子节点对应坐标$x^{1}$小于切分点子区域，右为大于，等于的划分为根结点。

• （2）重复：重复对子区域执行上述切割。

• （3）直到两个字区域没有实例存在时停止。

• 例子
  
  

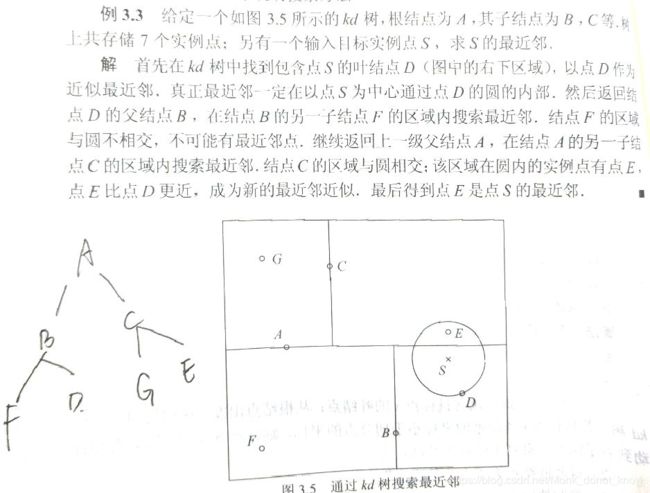
3.3.2 搜索Kd树

输入：已构造好的树，目标x
输出：x的最近邻点

1. 在kd树找出包含目标点x的叶节点：从根结点出发，递归向下访问kd树。若目标x当前维的坐标小于切分点，则移动到左子结点，反之右子节点，直到子节点问根结点。
2. 以此叶节点为“当前最近点”。
3. 递归向上回退，在每个结点进行以下操作：
   1. 如果该结点保存的实例点比当前最近点距离目标更近，则以该实例点为“当前最近点”。
   2. 当前最近点一定存在于费结点一个子节点对应的区域，检查该子节点的父节点的另一子节点对应的区域是否有更近点。如果是，则移动到另一个子节点。
4. 当退回根结点时候，搜索结束。最后的‘当前最近点“即为结果。

• kd树适合训练实例远大于空间维数
• 实例点随机分布时候，平均计算复杂度O(logN)
• 例子：
  

3.4 调包怪上线（transfer 实现KNN）

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

# data
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']

data = np.array(df.iloc[:100, [0, 1, -1]])
X, y = data[:,:-1], data[:,-1]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

from sklearn.neighbors import KNeighborsClassifier
model = KNeighborsClassifier()
model.fit(X_train, y_train)

model.score(X_test, y_test)

3.5 高逼格上线（遍历所有数据）

import numpy as np
from math import sqrt
import pandas as pd
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from collections import Counter

# 载入数据并设置标签和索引列
iris = load_iris()
df = pd.DataFrame(iris.data,columns=iris.feature_names)
df['label']=iris.target
df.columns = ['sepal length','sepal width','petal length','petal width','label']

# 这里只是取了前100个数据，并且只去两个特征做分类依据
data = np.array(df.iloc[:100,[0,1,-1]])
x,y = data[:,:-1],data[:,-1] 
x_train,x_test,y_train,y_test = train_test_split(x,y,train_size=0.8)

class KNN:
    def __init__(self,x_train,y_train, n_neighbors=3, p=2):
        """
        p=2是欧式距离
        n=3表示KNN的K=3，喔，这个K一定要设置为奇数啊
        """
        self.n = n_neighbors
        self.p = p
        self.x_train = x_train
        self.y_train = y_train
    
    def predict(self,x):
        #设置一个空列表,取n个点
        knn_list = []
        
        # 这里有np.linalg.norm的用法
        # https://blog.csdn.net/Monk_donot_know/article/details/88816863
        # 先取n_neighbers个点，放入空列表
        for i in range(self.n):
            dist = np.linalg.norm(x-self.x_train[i],ord=self.p)
            knn_list.append((dist,self.y_train[i]))
        
        # 再取剩下的n-n_neighbers个点，然后与n_neihbers个点比大小，将距离大的点更新出
        # 局，保证knn_list里面是距离小的点。
        for i in range(self.n,len(self.x_train)): 
            max_index = knn_list.index(max(knn_list,key=lambda x : x[0]))
            dist = np.linalg.norm(x-self.x_train[i],ord = self.p)
            if knn_list[max_index][0]> dist:
                knn_list[max_index] = (dist,self.y_train[i])
                        
        # 数一下分类最多的类是几，确定预测数据x的分类
        knn = [k[-1] for k in knn_list]
        counts = Counter(knn)
        x_type = sorted(counts,key=lambda x : x)[-1]
        
        return x_type
    
    # 这个score就是一个预测正确率.............
    def score(self,x_test,y_test):
        right_counts = 0
        for x , y in zip(x_test,y_test):
            label = self.predict(x)
            if label == y:
                right_counts += 1
        return right_counts/len(x_test)
       

来看看效果

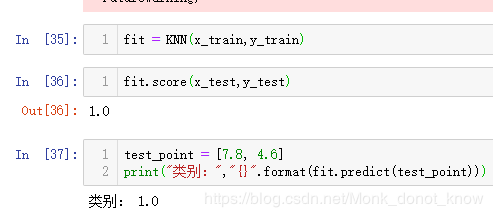
嗯，在测试集表现太不好，哈哈，100%的正确率
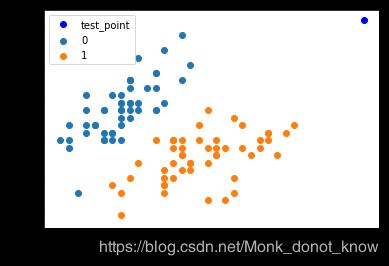
这个是二维的数据，可以直接画个散点图看看

plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')
plt.plot(test_point[0], test_point[1], 'bo', label='test_point')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

3.6 高高高逼格的KDT