不得不说的opencv 那些事

初次接触图像类的代码编辑，有很多新奇的东西值得去探讨研磨，在opencv 代码库编辑环境下，初次认知了图像代码处理的最基本的知识。

1.矩阵和图像的关系

在opencv 中，Mat 一个矩阵即为生成了一个图像，可对这个矩阵进行Imshow(),imread()等图像处理。以单通道的灰度图为例，矩阵中每一个数值对应图像中一个像素点的灰度值，矩阵中这些数值的有序排布就构成了一个图像。

Mat m1 = Mat::eye(500, 500, CV_64FC1);
//cout << m1 << endl;
imshow("www", m1);
waitKey(0);

以上代过编辑一个单位矩阵并输出，可以看到输出的图形恰为对角线为亮线的图形。

同样，读入一个图片，也可以输出这个图片任意一点的像素值。

Mat img = imread("pic.jpg", 0);				//读入一个单通道的灰度图
cout << img.type() << endl;					//输出图片像素的数据类型
cout << (int)img.at(1, 1) << endl;		//输出这个图片在(1, 1)点的像素值
imshow("www",img);
waitKey(0);

2.矩阵的基本运算

opencv 中定义了基本的矩阵运算函数和运算符重载，以便于用户进行图像的操作.

int row = 5;
//创建一个单位矩阵
Mat img = Mat::eye(5, 5, CV_64FC1);
cout << img << endl << endl;

//分别创建元素都为0和都为1的矩阵
Mat imagezeros = Mat::zeros(row, 5, CV_64FC1);
Mat imageones = Mat::ones(5, 5, CV_64FC1);
	
//可以直接进行像素元素的相乘
Mat img2 = img*imageones + 1;
cout << img2 << endl << endl;

//把一个图像元素内容拷贝到另一图像中
img.copyTo(img2);
cout << img2 << endl << endl;
//求一个图像矩阵的逆矩阵
cout << img.inv() << endl;

3.对图像矩阵的求导

以单通道的图片为例，对图像的像素点进行x方向求导，可以得到图像在这个点x方向的明亮强度变化的大小。同时图像梯度: G(x,y) = dx(i,j) + dy(i,j)，通过导数可以得到这个点的明暗梯度大小。求导公式: dx(i,j) = I(i+1,j) - I(i,j)， dy(i,j) = I(i,j+1) - I(i,j)

Mat img = imread("pic.jpg", 0);
 cout << "row  " << img.rows << "  col  " << img.cols << endl;

 Mat dimg1 = Mat(img.rows, img.cols-2, CV_8UC1);
 Mat dimg2 = Mat(img.rows, img.cols-2, CV_8UC1);

 /*
 *第一种方法，直接求导并存储
 */
 for( int i = 0; i < img.rows; i++)
 {
  for(int j = 1; j < img.cols - 1; j++)
  {
   dimg1.at(i , j-1) = img.at(i, j-1) - img.at(i , j + 1);
  }
 }

 /*
 *第二种方法,定义卷积模板实现
 */
 Mat model = Mat(1, 3, CV_64FC1);
 model.at(0, 0) = 1;
 model.at(0, 1) = 0;
 model.at(0, 2) = -1;

 for (int i = 0; i(i + m, j + n))*model.at(m, n + half);//(double)为强制转化成double类型
    }
   }
    dimg2.at(i, j - 1) = (uchar)sum;
  }
 }

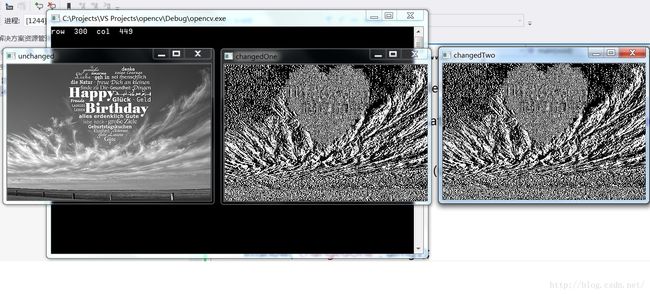
 imshow("unchanged", img);
 imshow("changedOne", dimg1);
 imshow("changedTwo", dimg2);
 waitKey(0);

把三幅图片放在一起来看

4.滤镜的出现和原理

滤镜就是一个矩阵，使用不同的滤镜不同的矩阵作为卷积核，对原图像进行卷积操作可以得到很多不同风格的效果，功能十分强大。

/*
*定义一个5*5的高斯模板矩阵, 并做归一化处理。
*/
Mat gauss(5, 5, CV_64FC1);
double sigma = 5;
for( int i = -2; i < 3; i++)
{
	for(int j = -2; j < 3; j++)
	{
		gauss.at(i + 2, j + 2) = exp(-(i*i + j*j)/(2*sigma*sigma));
	}
}
double gssum = sum(gauss).val[0];
for( int i = -2; i < 3; i++)
{
	for(int j = -2; j < 3; j++)
	{
		gauss.at(i + 2, j + 2)/=gssum;
	}
}
//cout << gauss << endl;
	
/*
*使用高斯模板分别在 x 和 y 两个方向上进行卷积操作
*/
Mat img = imread("pic.jpg", 0);
Mat dimg = Mat(img.rows - 4, img.cols - 4, CV_8UC1);
for( int i = 2; i < img.rows-2; i++)
{
	for( int j = 2; j < img.cols-2; j++)
	{
		double sum = 0;
		for( int m = 0; m < gauss.rows; m++)
		{
			for( int n= 0; n < gauss.cols; n++)
			{
				sum += (double)img.at(i + m - 2, j + n -2)*gauss.at(m, n);
			}
		}
	dimg.at(i-2, j-2) = (uchar)sum;
	}
}
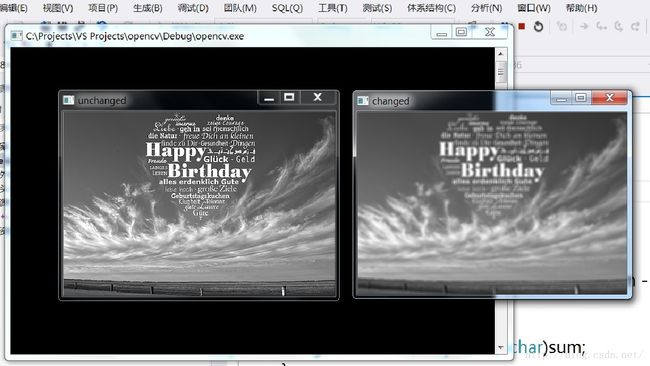
imshow("unchanged", img);
imshow("changed", dimg);
waitKey(0);

代码的效果清晰可见