基于word2vec的中文词向量训练
基于word2vec的中文词向量训练
使用katex解析的数学公式,csdn好像不支持
word2vec来源
-
Google开源
-
可以在百万数量级的词典和上亿的数据集上进行高效地训练
-
该工具得到的训练结果--
词向量(word embedding),可以很好地度量词与词之间的相似性
基本知识
激活函数
-
神经网络中处理非线性数据
-
饱和
当一个激活函数h(x)满足[\lim_{n\to +\infty} h’(x)=0]时我们称之为右饱和。
当一个激活函数h(x)满足[\lim_{n\to -\infty} h’(x)=0]时我们称之为左饱和。当一个激活函数,既满足左饱和又满足又饱和时,我们称之为饱和。
-
硬饱和与软饱和
对任意的(x),如果存在常数(c),当(x > c)时恒有 (h’(x) = 0)则称其为右硬饱和,当(x < c)时恒 有(h’(x)=0)则称其为左硬饱和。若既满足左硬饱和,又满足右硬饱和,则称这种激活函数为硬饱和。但如果只有在极限状态下偏导数等于0的函数,称之为软饱和。
Sigmoid 函数
-
神经网络中常用的
激活函数 -
Sigmoid函数函数定义:
[F(x)=\frac{1}{1+e^{-x}}] -
函数性质
导数可以用自身的形式来表达
[F’(x)=\frac{e{-x}}{(1+e{-x})^2}=F(x)(1-F(x))]
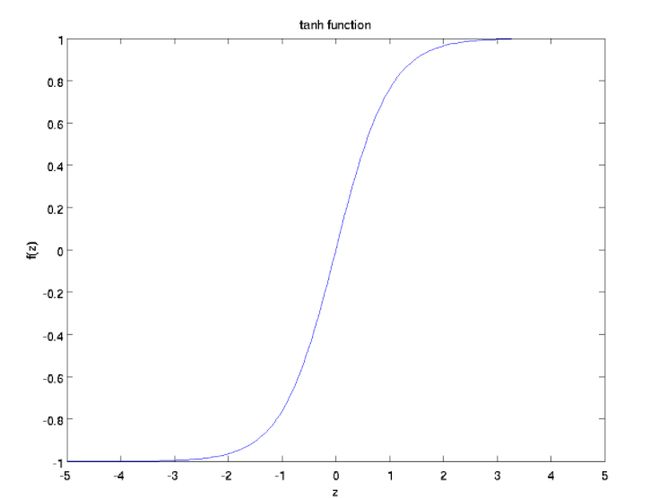
Tanh 函数
-
Tanh是Sigmoid的变形,与sigmoid不同的是,tanh是0均值的。因此,实际应用中,tanh会比sigmoid更好。 -
Tanh函数函数定义:
[F(x)=\frac{ex-e{-x}}{ex+e{-x}}=2sigmoid(2x)-1] -
函数导数
[F’(x)=1-F(x)^2]
逻辑回归
设 ({(x_i,y_i)}_{i=1}^m) 为一个二分类问题的样本数据,其中(x_i \in R^n,y_i \in {0,1}),当(y_i=1)时称相应的样本为 正例 ,当(y_i=0)时称相应的样本为 负例 。
利用 Sigmoid函数,对于任意样本(x=(x_1,x_2,…,x_n)^T),可将二分类问题的hypothesis函数 写成:
[h_θ(x)=δ(θ_0+θ_1x_1+θ_2x_2+…+θ_nx_n)]
其中,(θ=(θ_0,θ_1,…,θ_n)^T) 为待定参数。符号简化,引入(x_0=1)将(x)扩展为((x_0,x_1,x_2,…,x_n)^T),将其仍记为(x)。于是,(h_θ)可简写为:
[h_θ(x)=δ(θTx)=\frac{1}{1+e{-θ^Tx}}]
取阈值(T=0.5),则二分类的判别公式为:
[y(x) = \begin{cases}
1 & h_θ(x) \geqq 0.5 \
0 & h_θ(x) < 0.5
\end{cases}
]
Bayes 公式
记 (P(A)),(P(B)) 分别表示事件 A 和事件B发生的概率,(P(A|B))表示事件B发生的情况下事件A发生的概率,(P(A,B))表示事件A,B同时发生的概率,则有:
[P(A|B)=\frac{P(A,B)}{P(B)},P(B|A)=\frac{P(A,B)}{P(A)}]
综上:
[P(A|B)=P(A)\frac{P(B|A)}{P(B)}]
Huffman 编码
背景模型
Statistical Language Model
-
自然语言处理中的一个基本问题:如何计算一段文本序列在某种语言下出现的概率?
-
统计语言模型
对于一段文本序列(S=w_1, w_2, … , w_T),它的概率可以表示为:
[P(S)=P(w_1, w_2, …, w_T)=\prod_{t=1}^Tp(w_t|w_1, w_2, …, w_{t-1})]
即将序列的联合概率转化为一系列条件概率的乘积。问题变成了如何去预测这些给定previous words下的条件概率(p(w_t|w_1,w_2,…,w_{t-1}))。利用Bayes公式,公式被分解为:
[P(S)=P(w_1^T)=p(w_1) \cdot p(w_2|w_1) \cdot p(w_3/w_1^2) \cdots p(w_T|w_1^{T-1})]
其中的条件概率 (p(w_),p(w_2|w_1),p(w_3/w_12),p(w_T|w_1{T-1}))就是语言模型的参数,如果全部参数已经算得,那么给定句子 (w_1^T) 即可算出对应的 (p(w_1^T))
N-gram Model
-
由于
Statistical Language Model巨大的参数空间,这样一个原始的模型在实际中并没有什么卵用(难以计算)。我们假定一个词出现的概率只与它前面固定数目的词相关,于是出现了其简化版本——Ngram模型 -
Ngram模型
[p(w_t|w_1, w_2, …, w_{t-1}) \approx p(w_t|w_{t-n+1}, …, w_{t-1})]
常见的如bigram模型((N=2))和trigram模型((N=3))。事实上,由于模型复杂度和预测精度的限制,我们很少会考虑(N>3)的模型(对于大小(N=200000)的词典,模型参数量级为((O(Nn))),即(>8\times10{15})。当(N=2)时,就有:
[p(w_t|w_1, w_2, …, w_{t-1}) \approx p(w_t|w_{t-1})]利用Bayes公式,变成:
[p(w_t|w_1, w_2, …, w_{t-1}) \approx p(w_{t-1},w_t)|p(w_{t-1})]语料库足够大时,近似于:
[p(w_t|w_1, w_2, …, w_{t-1}) \approx count(w_{t-1},w_t)|count(w_{t-1})]我们可以用最大似然法去求解Ngram模型的参数——等价于去统计每个Ngram的条件词频。
利用
最大似然,把目标函数设为:
[\prod_{w \in c}p(w|Context(w))] 其中(c)表示语料(训练的文本内容),(Context(w))表示词(w)的上下文(Context),即(w)周边的词的集合。对于 n-gram 模型,就有(Context(w)=w_{i-n+1}^{i-1})实际应用一般采用
最大对数似然,即把目标函数设为:
[\sum_{w \in c}logp(w|Context(w))] 然后对函数进行最大化。此时,概率(p(w|Context(w))) 已被视为关于(w)和(Context(w))的函数,即:
[p(w|Context(w))=F(w,Context(w),θ)] 其中(θ)为待定参数集。所以,只要优化得到最优参数集(θ)后,(F)也被唯一确定了,以后任何概率(p(w|Context(w)))都可以通过函数(F(w,Context(w),θ))来计算。这样最关键的地方就是在于函数F的构造了。
Neural Network Language Model
-
基本思想
-
假定词表中的每一个word都对应着一个连续的特征向量;
-
假定一个连续平滑的概率模型,输入一段词向量的序列,可以输出这段序列的联合概率;
-
同时学习词向量的权重和概率模型里的参数。
-
-
模型
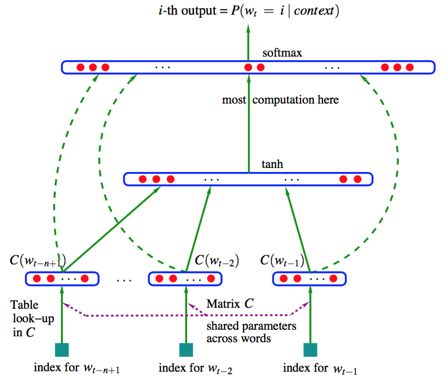
- 首先是一个线性的embedding层。它将输入的(N-1)个
one-hot词向量,通过一个共享的(D \times V)的矩阵(C),映射为(N-1)个分布式的词向量(distributed vector)。其中,(V)是词典的大小,(D)是embedding向量的维度(一个先验参数)。(C)矩阵里存储了要学习的word vector。 - 其次是一个简单的前向反馈神经网络(g)。它由一个tanh隐层和一个softmax输出层组成。通过将embedding层输出的(N-1)个词向量映射为一个长度为(V)的概率分布向量,从而对词典中的word在输入context下的条件概率做出预估:[p(w_i|w_1,w_2,…,w_{t-1}) \approx f(w_i, w_{t-1}, …, w_{t-n+1}) = g(w_i, C(w_{t-n+1}), …, C(w_{t-1}))]
- 首先是一个线性的embedding层。它将输入的(N-1)个
词向量
-
在
NLP中如何将自然语言数学化? -
one-hot representation
向量中每一个元素都关联着词库中的一个单词,指定词的向量表示为:其在向量中对应的元素设置为1,其他的元素设置为0。
比如:
“话筒”表示为 [0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 …]
“麦克”表示为 [0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 …] -
distributed representation
通过训练将某种语言中的每一个词映射成一个固定长度的短向量(当然这里的“短”是相对于
one-hot representation的“长”而言的),将所有这些向量放在一起形成一个词向量空间,而每一向量则为该空间中的一个点,在这个空间上引入“距离”,则可以根据词之间的距离来判断它们之间的(词法、语义上的)相似性了。-
Bag of Words Hypothesis
一篇文档的词频(而不是词序)代表了文档的主题。
基于Bag of Words Hypothesis,我们可以构造一个term-document矩阵(A):矩阵的行(A_{i,:})对应着词典里的一个word;矩阵的列(A_{:,j})对应着训练语料里的一篇文档;矩阵里的元素(A_{ij})代表着word (w_i)在文档(D_j)中出现的次数(或频率)。那么,我们就可以提取行向量做为word的语义向量(不过,在实际应用中,我们更多的是用列向量做为文档的主题向量)。
-
Distributional Hypothesis
上下文环境相似的两个词有着相近的语义。
同上,我们可以基于Distributional Hypothesis构造一个word-context的矩阵。此时,矩阵的列变成了context里的word,矩阵的元素也变成了一个context窗口里word的共现次数。
-
word2vec使用的模型
CBoW & Skip-gram Model
-
NNLM的问题-
同Ngram模型一样,NNLM模型只能处理定长的序列。
-
NNLM的训练太慢了,需要花费的时间太多。
-
-
NNLM模型的训练拆分-
用一个简单模型训练出连续的词向量;
-
基于词向量的表达,训练一个连续的Ngram神经网络模型。而NNLM模型的计算瓶颈主要是在第二步。
-
-
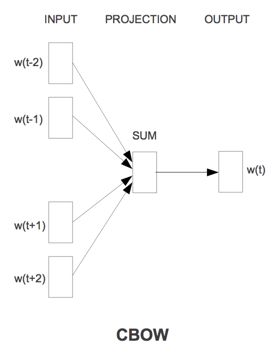
CBoW模型(Continuous Bag-of-Words Model)
-
我们对原始的NNLM模型做如下改造:
- 移除前向反馈神经网络中非线性的hidden layer,直接将中间层的embedding layer与输出层的softmax layer连接;
- 忽略上下文环境的序列信息:输入的所有词向量均汇总到同一个embedding layer;
- 将future words纳入上下文环境
-
-
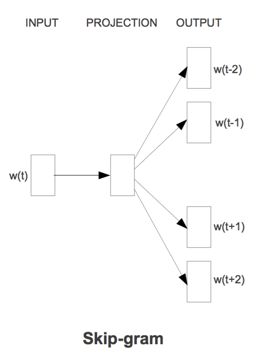
Skip-gram模型
从target word对context的预测中学习到word vector
如果将Skip-gram模型的前向计算过程写成数学形式,我们得到:[p(w_o|w_i)=\frac{e^{U_o \cdot V_i}}{\sum_j{e^{U_j \cdot V_i}}}]其中,(V_i)是embedding层矩阵里的列向量,也被称为(w_i)的input vector。(U_j)是softmax层矩阵里的行向量,也被称为(w_j)的output vector。
因此,Skip-gram模型的本质是
计算输入word的input vector与目标word的output vector之间的余弦相似度,并进行softmax归一化.
优化
Hierarchical Softmax
-
基本思想
将复杂的归一化概率分解为一系列条件概率乘积的形式:
[p(v|context)=\prod_{i=1}^m{p(b_i(v)|b_1(v), …, b_{i-1}(v), context)}]
其中,每一层条件概率对应一个二分类问题,可以通过一个简单的逻辑回归函数去拟合。这样,我们将对(V)个词的概率归一化问题,转化成了对(\log{V})个词的概率拟合问题。 -
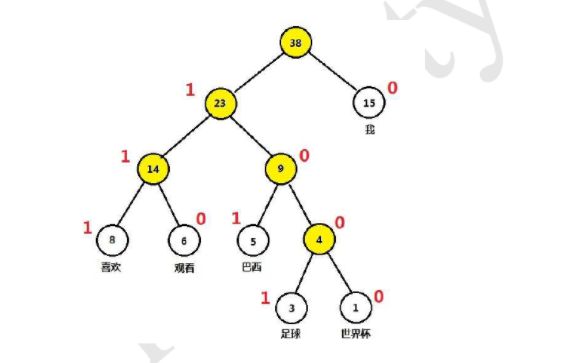
构造分类二叉树
我们可以通过构造一颗分类二叉树来直观地理解这个过程。首先,我们将原始字典(D)划分为两个子集(D_1)、(D_2),并假设在给定context下,target word属于子集(D_1)的概率(p(w_t \in D_1|context))服从logistical function的形式:
[p(w_t \in D_1|context)=\frac{1}{1+e^{-U_{D_{root}} \cdot V_{w_t}}}]
其中,(U_{D_{root}})和(V_{w_t})都是模型的参数。接下来,我们可以对子集(D_1)和(D_2)进一步划分。重复这一过程,直到集合里只剩下一个word。这样,我们就将原始大小为(V)的字典(D)转换成了一颗深度为(\log V)的二叉树。树的叶子节点与原始字典里的word一一对应;非叶节点则对应着某一类word的集合。显然,从根节点出发到任意一个叶子节点都只有一条唯一路径——这条路径也编码了这个叶子节点所属的类别。
同时,从根节点出发到叶子节点也是一个随机游走的过程。因此,我们可以基于这颗二叉树对叶子节点出现的似然概率进行计算。例如,对于训练样本里的一个target word (w_t),假设其对应的二叉树编码为({1, 0, 1, …, 1}),则我们构造的似然函数为:
[p(w_t|context)=p(D_1=1|context)p(D_2=0|D_1=1) \cdots p(w_t|D_k=1)]
乘积中的每一项都是一个逻辑回归的函数。
Negative Sampling
负采样的思想最初来源于一种叫做Noise-Contrastive Estimation的算法[6],原本是为了解决那些无法归一化的概率模型的参数预估问题。与改造模型输出概率的层次Softmax算法不同,NCE算法改造的是模型的似然函数。
以Skip-gram模型为例,其原始的似然函数对应着一个Multinomial的分布。在用最大似然法求解这个似然函数时,我们得到一个cross-entropy的损失函数:
[J(\theta)=-\frac{1}{T}\sum_{t=1}^T{\sum_{-c \leq j \leq c, j \neq 0}{\log p(w_{t+j}|w_t)}}]
式中的(p(w_{t+j}|w_t))是一个在整个字典上归一化了的概率。
而在NCE算法中,我们构造了这样一个问题:对于一组训练样本,我们想知道,target word的出现,是来自于context的驱动,还是一个事先假定的背景噪声的驱动?显然,我们可以用一个逻辑回归的函数来回答这个问题:
[p(D=1|w, context)=\frac{p(w|context)}{p(w|context)+kp_n(w)}=\sigma (\log p(w|context) - \log kp_n(w))]
这个式子给出了一个target word (w)来自于context驱动的概率。其中,(k)是一个先验参数,表明噪声的采样频率。(p(w|context))是一个非归一化的概率分布,这里采用softmax归一化函数中的分子部分。(p_n(w))则是背景噪声的词分布。通常采用word的unigram分布。
通过对噪声分布的(k)采样,我们得到一个新的数据集:。其中,label标记了数据的来源(真实数据分布还是背景噪声分布?)。在这个新的数据集上,我们就可以用最大化上式中逻辑回归的似然函数来求解模型的参数。
而Mikolov在2013年的论文里提出的负采样算法, 是NCE的一个简化版本。在这个算法里,Mikolov抛弃了NCE似然函数中对噪声分布的依赖,直接用原始softmax函数里的分子定义了逻辑回归的函数,进一步简化了计算:
[p(D=1|w_o, w_i)=\sigma (U_o \cdot V_i)]
此时,模型相应的目标函数变为:
[J(\theta) = \log \sigma(U_o \cdot V_i) + \sum_{j=1}^k{E_{w_j \sim p_n(w)}[\log \sigma(- U_j \cdot V_i)]}]
除了这里介绍的层次Softmax和负采样的优化算法,Mikolov在13年的论文里还介绍了另一个trick:下采样(subsampling)。其基本思想是在训练时依概率随机丢弃掉那些高频的词:
[p_{discard}(w) = 1 - \sqrt{\frac{t}{f(w)}}]
其中,(t)是一个先验参数,一般取为(10^{-5})。(f(w))是(w)在语料中出现的频率。
实验证明,这种下采样技术可以显著提高低频词的词向量的准确度。
以 gensim 訓練中文詞向量
-
获取中文维基数据,维基百科:资料库下载
文件名:zhwiki-latest-pages-articles.xml.bz2
-
从文件中提取文章
import logging from gensim.corpora import WikiCorpus def main(): path = './zhwiki-latest-pages-articles.xml.bz2' logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO) wiki_corpus = WikiCorpus(path, dictionary={}) texts_num = 0 with open("wiki_texts.txt", 'w', encoding='utf-8') as output: for text in wiki_corpus.get_texts(): output.write(' '.join(text) + '\n') texts_num += 1 if texts_num % 10000 == 0: logging.info("已处理 %d 篇文章" % texts_num) if __name__ == "__main__": main() -
使用
opencc将文章统一转换为简体中文-
opencc下载地址
-
繁体转简体
opencc -i wiki_texts.txt -o wiki_zh.txt -c t2s.json
-
-
使用 jieba分词 对中文进行分词
import jieba import logging def main(): logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO) jieba.set_dictionary('jieba_dict/dict_zh.txt.big') stop_word_set = set() with open('jieba_dict/stopwords_zh.txt', 'r', encoding='utf-8') as sw: for line in sw: stop_word_set.add(line.strip('\n')) texts_num = 0 output = open('wiki_seg.txt', 'w', encoding='utf-8') with open('wiki_zh.txt', 'r', encoding='utf-8') as content: for line in content: line = line.strip('\n') words = jieba.cut(line, cut_all=False) for word in words: if word not in stop_word_set: output.write(word + ' ') texts_num += 1 if texts_num % 10000 == 0: logging.info("已完成前 %d 行的分词" % texts_num) output.close() if __name__ == '__main__': main() -
使用
gensim的word2vec模型对语料进行训练import logging from gensim.models import word2vec def main(): logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO) sentences = word2vec.Text8Corpus("wiki_seg.txt") model = word2vec.Word2Vec(sentences, size=250) model.save("med250.model.bin") if __name__ == "__main__": main()