13行Python代码实现一个神经网络（Part 2 - 梯度下降法）

Declaration: 本文翻译自iammask的blog，原作者保留本文知识产权，转载请注明出处。
Part 1 “一个 11 行 Python 代码实现的神经网络（第一部分）”的翻译可以在此处找到

摘要：本文主要通过一个简单的例子和python实现讲解梯度下降法。
后续：我会继续尝试利用现有的算法（比如Dropout，DropConnect，和Momentum）为本文的例子加入一些有趣的特性。感兴趣可以关注我的tweeter @iamtrask

首先， 我们直接给出代码

import numpy as np
X = np.array([ [0,0,1],[0,1,1],[1,0,1],[1,1,1] ])
y = np.array([[0,1,1,0]]).T
alpha,hidden_dim = (0.5,4)
synapse_0 = 2*np.random.random((3,hidden_dim)) - 1
synapse_1 = 2*np.random.random((hidden_dim,1)) - 1
for j in xrange(60000):
    layer_1 = 1/(1+np.exp(-(np.dot(X,synapse_0))))
    layer_2 = 1/(1+np.exp(-(np.dot(layer_1,synapse_1))))
    layer_2_delta = (layer_2 - y)*(layer_2*(1-layer_2))
    layer_1_delta = layer_2_delta.dot(synapse_1.T) * (layer_1 * (1-layer_1))
    synapse_1 -= (alpha * layer_1.T.dot(layer_2_delta))
    synapse_0 -= (alpha * X.T.dot(layer_1_delta))

Part 1: 优化
在本文的Part 1中，我利用一个简单的神经网络讲解了反向传播的基础原理。反向传播使得我们能衡量整个网络中每个权值对整体误差的影响，同时，也能使我们使用算法去更新这些权值。这个算法就是，梯度下降法。

读者需要了解的一个要点是，反向传播并不能最优化权值。它仅仅是将网络输出层的误差信息反馈至网络中所有的权值，从而我们可以使用算法优化这些权值使网络的输出结果与真实结果相符。实际上，人们已经开发了大量的非线性优化算法优化权值。

一些典型的算法有（译注-原文中有链接，感兴趣的可以继续深入研究这些算法）：
• Annealing
• Stochastic Gradient Descent
• AW-SGD (new!)
• Momentum (SGD)
• Nesterov Momentum (SGD)
• AdaGrad
• AdaDelta
• ADAM
• BFGS
• LBFGS

这些算法的性能比较如下：
• ConvNet.js
• RobertsDionne

不同场景下，我们可以选择不同的优化算法，在某些情况下，这些算法还可以叠加使用。本文中，我们将研究梯度下降法。这也是最简单，最广泛应用的的神经网络优化算法。在接下来的例子中，我们可以看到，梯度下降对参数的优化使得我们的神经网络更加强大。

Part 2: 梯度下降法
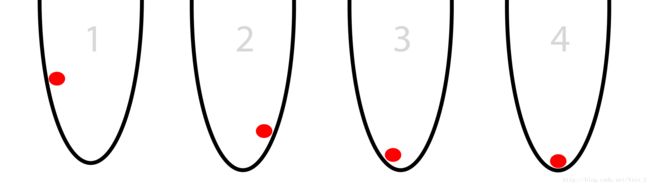
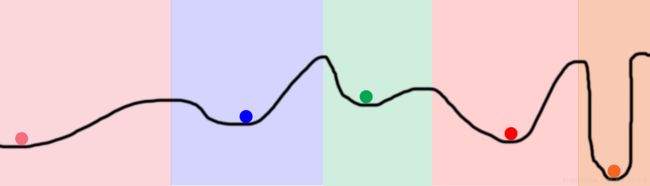
如下图所示，想象在一个圆桶中有一个红色的球，这个球尝试着找到桶底。这，就是最优化。本例中，球不停的优化自己的位置（从左到右）从而找到桶的最低点。（这里暂停一下，确定你了解了最后一句话）

为使这个例子更加游戏化一点，我们假设这个球有两个选择：向左或者向右，且球的最终目标是降低到尽可能低的位置。
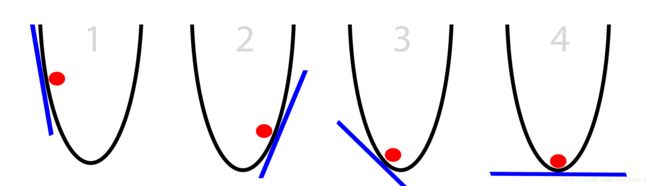
在这个游戏中，球唯一掌握的信息是“其当前位置处桶壁的斜率”，如下图蓝色线所示。

注意到，当斜率为正时，球应该向左移动，反之当斜率为负时，球应向右移动。这个性质足以使在数次迭代后，球能找到最低的位置。这就是最优化的一个子领域：梯度优化。其中，梯度是斜率，坡度的更严谨的表达。

总结上例，我们可以得出一个简单的梯度下降算法：
1. 为当前位置计算梯度；
2. 梯度为负，向右移动；
3. 梯度为正，向左移动；
4. 重复，直至梯度为0。

然而，还有一个需要注意的问题：“球每次移动多少才合适？”。让我们重新观察圆桶，可以看出，坡度越大的地方离底部越远。显然，我们可以利用这个观察结果进一步提升以上算法性能。同时，我们假设这个桶在一个 (x,y) 平面上，球的位置用一个 xb 表示（译注：球只在桶壁移动，因此 yb 是 xb 的函数， xb 确定则球位置 (xb,yb) 唯一确定）。因此，增加 xb 相当于向右移动，减小 xb 相当于向左移动，我们最终的目标是使得 xb=0 。我们的算法也可以更新为：

1. 对当前位置 xb 计算梯度；
2. 用负梯度值更新 xb ，即 xb=xb− 梯度。
3. 重复，直至梯度为0。

这个更新算法是对我们原本算法相当大的改进。在进一步阅读前，请确保你已经在脑海中描绘出以上算法描绘的球的运动轨迹。对于所有的正梯度，球会向左移动，对于所有的负梯度，球会向右移动；梯度的绝对值越大，球移动的越快。从而，最终球会落入最低点，这个最低点也被称为“收敛点”。

Part 3: 有些情况下，算法并不适用
梯度下降法并不是完美的。本节中，我们探讨梯度下降的问题，以及人们如何解决这些问题。这个过程将会帮助我们进一步优化我们的神经网络。

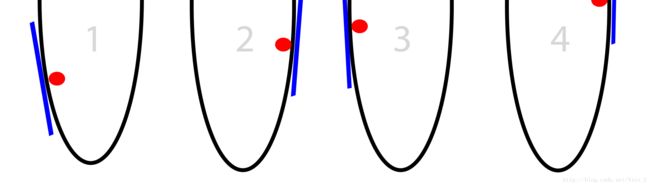
Problem1： 梯度过大

在我们的算法中，每一次位置的移动量是梯度的大小。这就有可能造成一种情况，梯度太大的时候我们可能会到达比我们初始位置相对于最低点更远的位置，而且随着迭代进行，我们可能离最低点越来越远。这种现象被称为“发散（divergence）”。下图很清晰的阐释了这个问题所在：

Solution 1：降步伐变小
这是一种很显然的解决方案，即，梯度太大，那我们就走慢点。我们定义一个0和1之间的小数 α ，每次的步伐由负梯度，变为 α *负梯度。因此，我们的算法变为

1. 对当前位置 xb 计算梯度；
2. 用负梯度值更新 xb ，即 xb=xb−α∗ 梯度。
3. 重复，直至梯度为0。

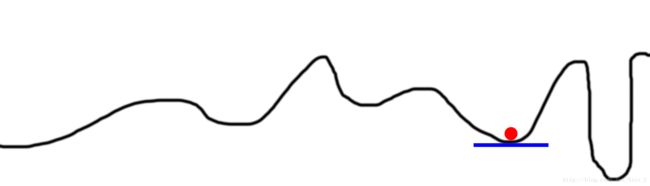
Problem 2：局部最小值

有些时候，我们的桶有着很奇怪的形状，比如下图。此时我们的算法可能并不会把我们带到全局最小值，而仅仅是一个局部最小值。

Solution 2： 多个随机起始状态

这是目前梯度下降法遇到的最困难的问题，而人们也提出了很多算法试图解决这一问题。总的来说，这些算法有一个共同点，他们都使用随机搜索尝试桶的不同区域。如下图所示，我们随机选取5个位置，理想情况下，这5个位置刚刚好落入5个不同颜色的区域。

在神经网络中，一种实现这种随机选取起始点的做法是“增加隐藏层维度”。同一层的每个隐藏节点从一个随机的位置开始，从而不同的隐藏节点收敛至不同形态。“Parameterizing this size”使得用户可以在一个神经网络中尝试成千上万（或者上百亿）种不同的局部最小值。

Sidenote 1: 这也是神经网络如此强大的原因所在。它能够搜寻的空间比他们实际计算的要广阔的多得多。如上例所示，我们用5个球/随机起点（理论上）和一些迭代就搜寻了整个桶壁上每一种状态。这远比遍历桶壁要来的更为高效。

Sidenote 2: 有些人也许会问，神经网络中随机的起始点会使得有点球落入用养的space，他们实际上是在浪费计算能力（因为总会收敛到统一状态）。是的，现有技术中避免这种情况的方案叫做“Dropout”和“DropConnect”。有兴趣的读者可以持续关注我的更新。

Problem 3：梯度过小

显然，梯度太小的时候，收敛可能会花很长很长的时间。另一方面，梯度太小（或者 α 太小）会使得球更容易落入局部最小值，比如下图

Solution 3: 增大 α

直觉上，我们可以增大 α 的值，有些时候， α 甚至可以大于1，但这情况很罕见。

Part 4： 神经网络中的SGD

在阅读了以上内容后，你也许会疑惑，这些跟神经网络和反向传播有什么关系尼？这是最困难也是最重要的的部分，因此请仔细理解。

实际上，在上例中，我们通过不断的调整球的位置（ x 的值）来达到桶的最底部（即达到 y 的最小值）；在神经网络中，我们期望通过不停的调整网络中的权值来最小化网络输出误差。因此，我们可以将球的位置（ x 轴）映射为网络中的权值，而将球的当前高度（ y 轴）映射为网络输出误差。
这样一来，球的运动过程其实就像一个2层神经网络。

• 2层神经网络（仅含输入输出层）

import numpy as np

# compute sigmoid nonlinearity
def sigmoid(x):
    output = 1/(1+np.exp(-x))
    return output

# convert output of sigmoid function to its derivative
def sigmoid_output_to_derivative(output):
    return output*(1-output)

# input dataset
X = np.array([  [0,1],
                [0,1],
                [1,0],
                [1,0] ])

# output dataset            
y = np.array([[0,0,1,1]]).T

# seed random numbers to make calculation
# deterministic (just a good practice)
np.random.seed(1)

# initialize weights randomly with mean 0
synapse_0 = 2*np.random.random((2,1)) - 1

for iter in xrange(10000):

    # forward propagation
    layer_0 = X
    layer_1 = sigmoid(np.dot(layer_0,synapse_0))

    # how much did we miss?
    layer_1_error = layer_1 - y

    # multiply how much we missed by the 
    # slope of the sigmoid at the values in l1
    layer_1_delta = layer_1_error * sigmoid_output_to_derivative(layer_1)
    synapse_0_derivative = np.dot(layer_0.T,layer_1_delta)

    # update weights
    synapse_0 -= synapse_0_derivative

print "Output After Training:"
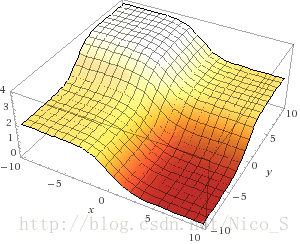
print layer_1

在这个网络中，输入层有两个节点，输出层有一个节点。因此，可调整的权值有两个，误差只有一个（代码第35行）。想象一个三维空间 (x,y,z) ， 其中 z 轴是误差， x,y 轴是两个权值。由代码第31，32，35行我们可以得出 z 与 x,y 的关系，从而画出下图。注意，对于 x,y 平面上的一点（即一组权值）， z 是对于所有4组训练输入的总误差。

此图中， x 和 y 分别是第一二个输入对应的权值。可以看出，误差与 x 轴正相关，即 x 越大误差越小。

---

译注：感觉此图有问题。首先，输入的四组数据是 [0,1;0,1;1,0;1,0] ，与权值矩阵 [x,y].T 相乘后，我们得到 [y,y,x,x].T 作为输出层的输入，在输出层我们用sigmoid函数处理后再减去真实输出矩阵 [0,0,1,1].T 得到误差矩阵为 [f(y),f(y),f(x)-1,f(x)-1].T ，其中我们用 f 函数表示sigmoid函数。从而，总误差 z=2/(1+exp(−x))+2/(1+exp(−y))−2 ，且很容易发现，总误差z的范围是从-2到2。

1) 如果直接画误差z，我们可以得到一个与原作者形状差不多的图，如下所示。可以看出，这个图相当于把原作者的图转了个方向，在我的图里， x,y 均与误差正相关，即 x,y 均取 ∞ 时，误差取最大值2； x,y 均取 −∞ 时，误差取最小值-2。这与原作者不同，不知道为什么。另外原作者的z轴全是正数，而且是从0到4，他是把-2到2加了2么？

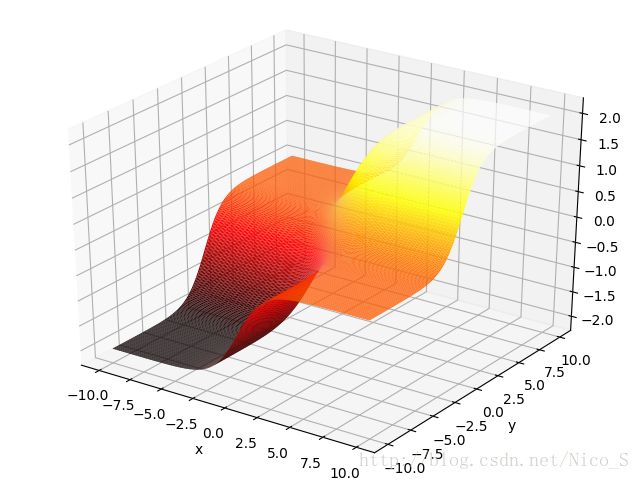
2) 如果我们不直接画z，而是画z的绝对值（我认为这个更合理，因为误差为-2的时候那也是很大的误差啊，我们应该是让z的绝对值尽可能小才对，而不是让z本身的值尽可能小）。这样画出的来的结果如下图，此图与原作者的图相去甚远，但我觉得更合理。

此时，我们不应该得出误差绝对值与x正相关的结论，因为就训练序列来看，虽然第一列与真实输出完全正相关，但是第二列也与真实输出完全负相关。我觉得最后的误差应该是x,y共同作用的结果，而不仅仅取决于第一列（即神经网络网络训练的结果应该是同时与x正相关与y负相关，而非仅仅依赖于x）

---