线性分类器之Fisher线性判别

在前文《贝叶斯决策理论》中已经提到，很多情况下，准确地估计概率密度模型并非易事，在特征空间维数较高和样本数量较少的情况下尤为如此。
实际上，模式识别的目的是在特征空间中设法找到两类（或多类）的分类面，估计概率密度函数并不是我们的目的。
前文已经提到，正态分布情况下，贝叶斯决策的最优分类面是线性的或者是二次函数形式的，本文则着重讨论线性情况下的一类判别准则——Fisher判别准则。

为了避免陷入复杂的概率的计算，我们直接估计判别函数式中的参数（因为我们已经知道判别函数式是线性的）。

首先我们来回顾一下线性判别函数的基本概念：
表达形式：

g(x)=ωTx+ω0

其中， x 是 d 维特征向量； ω 称为权向量，决定分类面的方向； ω0 是个常数，称为阈权值。

x=[x1,x2,...,xd]T,ω=[ω1,ω2,...,ωd]T

关于 ω 和 ω0 的作用，大家可以考虑一下二维空间，则其分别对应于斜率和截距，事实上，高维空间亦是如此。

对于两类问题的决策规则：
令 g(x)=g1(x)−g2(x) （分别为第一类和第二类的判别函数，具体定义见前文），则

g(x)>0,x∈ω1

g(x)<0,x∈ω2

g(x)=0,x可归入任意一类，或者拒绝

可以看出，方程 g(x)=0 定义了一个决策面，它把归类于 ω1 类的点和归类于 ω2 的点分割开来，从而完成分类的目的。

Fisher线性判别：
Fisher决策的出发点是：把所有的样本都投影到一维空间，使得在投影线上最易于分类 。
那什么是最易于分类的投影面呢？我们希望这个投影面是这样的：
投影后两类相隔尽可能远，而对同一类的样本又尽可能聚集。

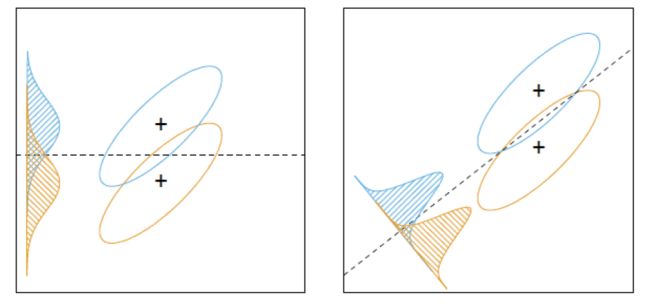
基于这个出发点，我们需要算出最佳的投影方向。如下图，右侧的投影面则优于左侧的投影面，因为它将两个类别更好地分开。

为了求出这个最佳投影面，我们要引入离散度矩阵的概念：
首先一些基本定义：
样本集： X={x1,x2,...,xN} ， ω1 类： X1={x11,x12,...,x1N} ， ω2 类： X2={x21,x22,...,x2N} ，投影函数： yi=ωTxi,i=1,2,...,N

离散度矩阵：

在 X 空间：
- 类均值向量：

mi=1NiΣxj∈Xixj,i=1,2

- 类内离散度矩阵：

Si=Σxj∈Xi(xj−mi)(xj−mi)T,i=1,2

- 总类内离散度矩阵：

Sw=P(ω1)S1+P(ω2)S2

- 类间离散度矩阵：

Sb=P(ω1)P(ω2)(m1−m2)(m1−m2)T

在 Y 空间：
- 类均值：

m∗i=1NiΣyj∈Yiyj,i=1,2

- 类内离散度矩阵：

S∗i=Σyj∈Yi(yj−m∗i)(yj−m∗i)T,i=1,2

- 总类内离散度矩阵：

S∗w=S∗1+S∗2

- 类间离散度矩阵：

S∗b=(m∗1−m∗2)2

Fisher准则函数：

maxJF(ω)=(m∗1−m∗2)S∗1+S∗2

实际上，Fisher准则函数就是使得类间离散度尽可能大，而类内离散度尽可能小，这样就能够使得两类之间尽可能分开，各类的内部又能尽可能聚集。

Fisher准则函数的求解：

带入 y=ωTx ，得

maxJF(ω)=ωTSbωωTSwω

ω∗:maxωJF(ω)

令分母 ωTSwω=c≠0 ，为常数，最大化分子，利用拉格朗日乘数法定理，有：

ω∗=S−1w(m1−m2)

确定了 ω 我们也就确定了决策面的方向，下一步计算阈权值 ω0 ：
（1）通常来讲，阈权值可以根据经验来选择：

ω0=−12(m∗1+m∗2)

ω0=−m∗

ω0=−12(m1+m2)TS−1W(m1−m2)−ln(P(ω1)P(ω2))

（2） d 和 N 很大时， y 近似正态分布，可在 Y 空间内用贝叶斯分类器确定 ω0 。