【python学习笔记】6:用Gauss-Legendre求积公式近似求积分值
高斯-勒让德求积公式给出了一个定积分的近似求法:
不妙的是这种求法对上下限要求为1和-1,但是因为积分可以变限,所以求任意定积分只要做变换就好:
用高斯公式求积分的近似值,精确度是非常高的,一般用几个点就可以得到很不错的近似值。这里用了三点高斯积分和五点高斯积分。
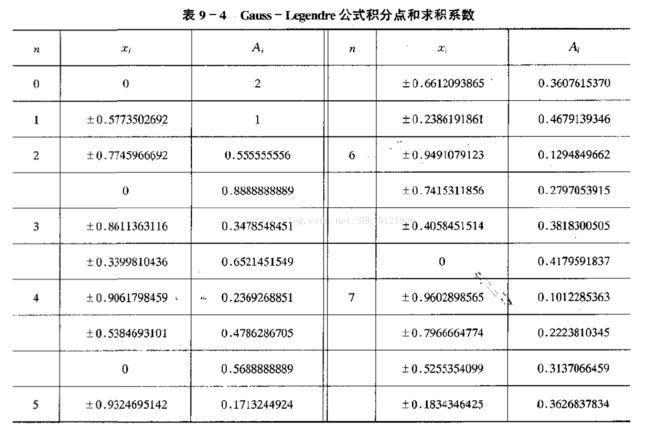
至于这些点怎么找,实际上它们是勒让德多项式的零点,因为这个我没学,老师直接给出了下面的高斯点表:
如要用三点高斯积分法,那么只要看n=2这个子表(因为n从0,1,2),用五点高斯积分法就只要看n=4这个子表了。
将xi和Ai带入到高斯求积公式里,就可以求得积分值了。
注意到xi总是唯一的,且对应着确定的一个Ai(权),所以我用字典(dictionary)来存三点高斯积分和五点高斯积分的高斯点-权表,然后遍历该表就可以实现累加了。
注意xi绝对值相同的时候总是对应相同的Ai,所以只要存正的就够了。
第一题描述:
*子问题①:任意在-1到1上有定义的函数从-1到1的积分
#求任意函数从-1到1的积分
import math
def fun(x):
return x*x
GauThree={0.7745966692:0.555555556,0:0.8888888889}
GauFive={0.9061798459:0.2369268851,0.5384693101:0.4786286705,0:0.5688888889}
GauSum=0.0
for key,value in GauThree.items():
if(key>0):
GauSum+=fun(key)*value
GauSum+=fun(-key)*value
else:
GauSum+=fun(key)*value
print ("GauThree Method:",GauSum)
GauSum=0.0
for key,value in GauFive.items():
if(key>0):
GauSum+=fun(key)*value
GauSum+=fun(-key)*value
else:
GauSum+=fun(key)*value
print ("GauFive Method:",GauSum)
本例求的是y=x^2从-1到1的定积分。
运行结果:
*子问题②:任意函数在合法区间上的积分
#任意区间上对函数的积分
import math
def fun(x):
return x*x
def main():
GauThree={0.7745966692:0.555555556,0:0.8888888889}
GauFive={0.9061798459:0.2369268851,0.5384693101:0.4786286705,0:0.5688888889}
GauSum=0.0
print ("Input a and b as two numbers(must promise a0):
GauSum+=fun(((a-b)*key+a+b)/2)*value
GauSum=GauSum*(b-a)/2
print ("GauThree Method:",GauSum)
GauSum=0.0
for key,value in GauFive.items():
GauSum+=fun(((b-a)*key+a+b)/2)*value
if(key>0):
GauSum+=fun(((a-b)*key+a+b)/2)*value
GauSum=GauSum*(b-a)/2
print ("GauFive Method:",GauSum)
main() 尝试求y=x^2从1到2的积分。
运行结果:
第二题描述:
*任意函数型曲线在合法区间上的第一类曲线积分
#任意区间上对函数的曲线积分
import math
def fun(x):
return x*x+2
#如果修改了fun函数,注意修改下面这个函数作为fun的导数dy/dx
def Dfun(x):
return 2*x
def main():
GauThree={0.7745966692:0.555555556,0:0.8888888889}
GauFive={0.9061798459:0.2369268851,0.5384693101:0.4786286705,0:0.5688888889}
GauSum=0.0
print ("Input a and b as two numbers(must promise a0):
GauSum+=fun(((a-b)*key+a+b)/2)*math.sqrt(1+Dfun(((a-b)*key+a+b)/2)**2)*value
GauSum=GauSum*(b-a)/2
print ("GauThree Method:",GauSum)
GauSum=0.0
for key,value in GauFive.items():
GauSum+=fun(((b-a)*key+a+b)/2)*math.sqrt(1+Dfun(((b-a)*key+a+b)/2)**2)*value
if(key>0):
GauSum+=fun(((a-b)*key+a+b)/2)*math.sqrt(1+Dfun(((a-b)*key+a+b)/2)**2)*value
GauSum=GauSum*(b-a)/2
print ("GauFive Method:",GauSum)
main()
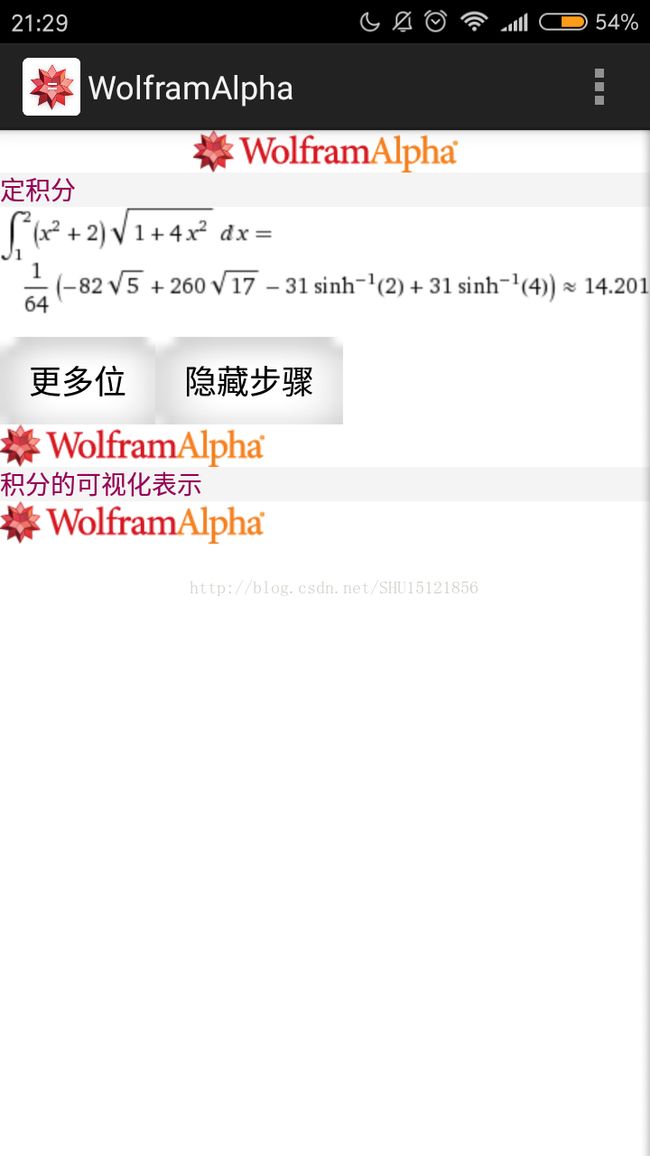
尝试求y=x^2+2在点A(1,3)到点B(2,6)上的第一类曲线积分。
运行结果:
这个积分比较复杂,验证一下是否正确(当然我已经只能依赖wolfram alpha了):
可以看到拟合的不错,高斯-勒让德求积公式很厉害。
在第一题里要改函数只要修改函数fun()所返回的值的表达式即可,在第二题里注意同时要修改Dfun()作为fun()函数的导数(在第一类曲线积分里要用到)。