Python——绘制简单分类器边界(决策树&SVM)

该绘制方法仅适用于因变量个数为两类的分类器。
可以用该绘图方法，直观的了解sklearn中分类器的参数的作用

1 准备工作

提取 iris数据中的有效特征

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier

dtree = DecisionTreeClassifier(max_depth = 3)
iris = load_iris()
x, y = iris.data, iris.target
dtree.fit(x, y)
# 用决策树方法看特征的重要性
dtree.feature_importances_
"""
array([0.        , 0.        , 0.58561555, 0.41438445])
发现仅有最后两个特征是有效的
"""

后续就采用iris的后面两个特征作图，画出分类器在数据集上的分类边界

2 汇总分类边界

# 加载包
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')


# 画出数据点和边界
def border_of_classifier(sklearn_cl, x, y):
        """
        param sklearn_cl : skearn 的分类器
        param x: np.array 
        param y: np.array
        """
        ## 1 生成网格数据
        x_min, y_min = x.min(axis = 0) - 1
        x_max, y_max = x.max(axis = 0) + 1
        # 利用一组网格数据求出方程的值，然后把边界画出来。
        x_values, y_values = np.meshgrid(np.arange(x_min, x_max, 0.01),
        np.arange(y_min, y_max, 0.01))
        # 计算出分类器对所有数据点的分类结果 生成网格采样
        mesh_output = sklearn_cl.predict(np.c_[x_values.ravel(), y_values.ravel()])
        # 数组维度变形  
        mesh_output = mesh_output.reshape(x_values.shape)
        fig, ax = plt.subplots(figsize=(16,10), dpi= 80)
        ## 会根据 mesh_output结果自动从 cmap 中选择颜色
        plt.pcolormesh(x_values, y_values, mesh_output, cmap = 'rainbow')
        plt.scatter(x[:, 0], x[:, 1], c = y, s=100, edgecolors ='steelblue' , linewidth = 1, cmap = plt.cm.Spectral)
        plt.xlim(x_values.min(), x_values.max())
        plt.ylim(y_values.min(), y_values.max())
        # 设置x轴和y轴
        plt.xticks((np.arange(np.ceil(min(x[:, 0]) - 1), np.ceil(max(x[:, 0]) + 1), 1.0)))
        plt.yticks((np.arange(np.ceil(min(x[:, 1]) - 1), np.ceil(max(x[:, 1]) + 1), 1.0)))
        plt.show()

3 观察参数

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC

## 载入数据
iris = load_iris()
x, y = iris.data[:, [2,3]], iris.target # 依据第一步决策时的重要性仅用后面两个特征

#### 1 观察决策时的max_depth 
dtree1 = DecisionTreeClassifier(max_depth = 2)
dtree2 = DecisionTreeClassifier(max_depth = 4)
dtree3 = DecisionTreeClassifier(max_depth = 20)
dtree1.fit(x, y)
dtree2.fit(x, y)
dtree3.fit(x, y)
border_of_classifier(dtree1, x, y)
border_of_classifier(dtree2, x, y)
border_of_classifier(dtree3, x, y)

max_depth = 2 的时候分界线如下，显然分类没有全分对，但是用这个模型去做预测的泛化能力会不错

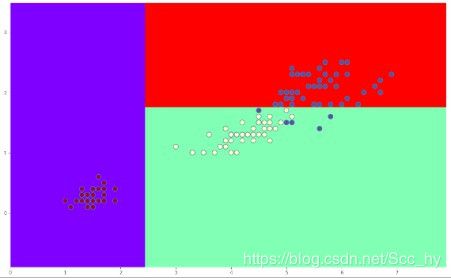
max_depth = 4 的时候分界线如下，仍有分类没有全分对，但是用这个模型去做预测的泛化能力不一定会有max_depth = 2 好

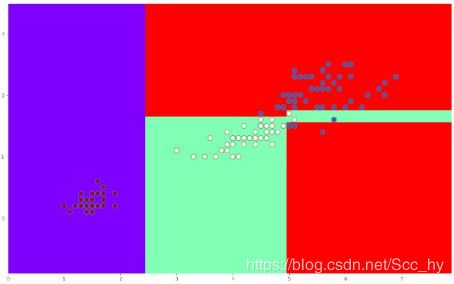
max_depth = 20 的时候分界线如下，显然全部分类都分对了，但是可以怀疑这个模型存在过拟合

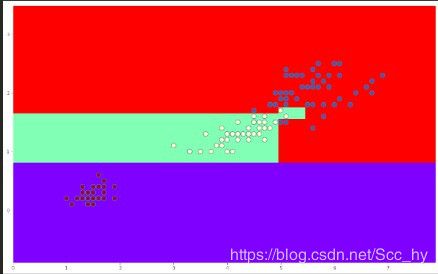
显然随着树深的增加 训练的分类器对训练集的分类准确率会逐步提高。

SVC 支持向量机 惩罚系数

#### 1 观察支持向量机惩罚系数 C
svc_line1 = SVC(C = 0.01, kernel='rbf')
svc_line2 = SVC(C = 5.0, kernel='rbf')
svc_line3 = SVC(C = 100.0, kernel='rbf')
svc_line1.fit(x, y)
svc_line2.fit(x, y)
svc_line3.fit(x, y)
border_of_classifier(svc_line1, x, y)
border_of_classifier(svc_line2, x, y)
border_of_classifier(svc_line3, x, y)

C = 0.01 的时候分界线如下

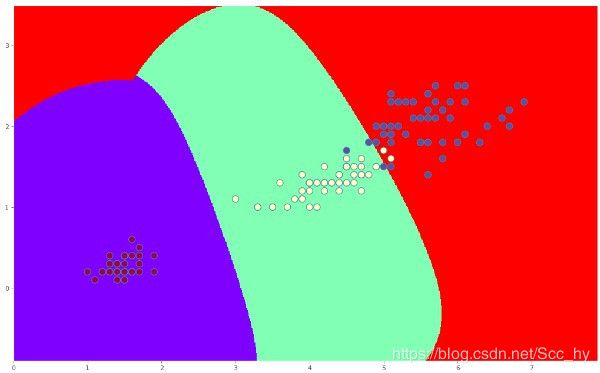
C = 5 的时候分界线如下

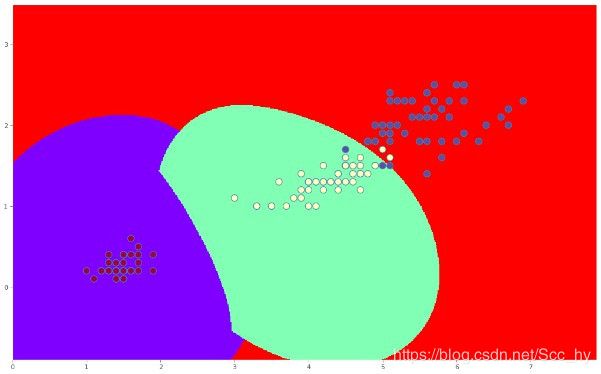
C = 100 的时候分界线如下

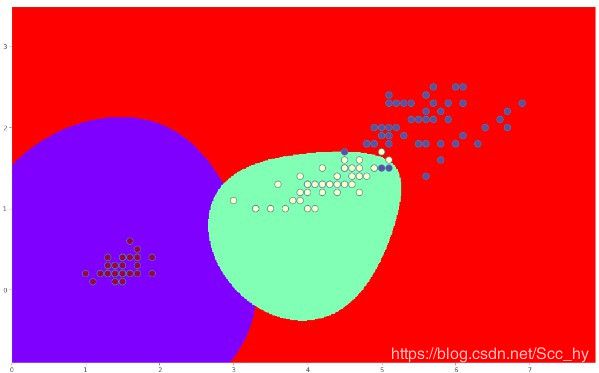
显然随着惩罚系数的增大，对数据错误的忍耐度更加低（类数据包裹的更紧）

上述的iris 数据集总体有点线性分布可能看的不明显，用非线性分布的数据集去看分类界限

# 生成数据
from sklearn.datasets import make_moons
mk_moons = make_moons(n_samples = 300, noise = 0.3)
m_x = mk_moons[0]
m_y = mk_moons[1]
def plot_moon(m_x, m_y):
    x_1 = [m_x[i][0] for i in range(len(m_x))]
    x_2 = [m_x[i][1] for i in range(len(m_x))]
    plt.scatter(x_1, x_2, c = m_y)
    plt.show()

plot_moon(m_x, m_y)

#### 1 观察支持向量机惩罚系数 C
svc_line1 = SVC(C = 0.1, kernel='poly', degree = 3, coef0 = 1)
svc_line2 = SVC(C = 1, kernel='poly', degree = 3, coef0 = 1)
svc_line3 = SVC(C = 5.0, kernel='poly', degree = 3, coef0 = 1)
svc_line4 = SVC(C = 120.0, kernel='poly', degree = 3, coef0 = 1)
svc_line1.fit(m_x, m_y)
svc_line2.fit(m_x, m_y)
svc_line3.fit(m_x, m_y)
svc_line4.fit(m_x, m_y)
"""
由于配色太难看了 笔者改成了太极色 -。-
plt.pcolormesh(x_values, y_values, mesh_output, cmap = 'gist_gray_r')
plt.scatter(x[:, 0], x[:, 1], c = y, s=100, edgecolors ='steelblue' , linewidth = 1, cmap = 'gist_gray')
"""

border_of_classifier(svc_line1, m_x, m_y)
border_of_classifier(svc_line2, m_x, m_y)
border_of_classifier(svc_line3, m_x, m_y)
border_of_classifier(svc_line4, m_x, m_y)

C = 0.01 的时候分界线如下

C = 1 的时候分界线如下

C = 5 的时候分界线如下

C = 120 的时候分界线如下

以上五个图看的更加显著 显然随着惩罚系数的增大，对数据错误的忍耐度更加低（类数据包裹的更紧）