降维算法学习之PCA理论推导

PCA算法简述

　　来，快上车，老铁。主成分分析(Principal Component Analysis, PCA)是最常用的线性降维方法，它是通过某种线性投影，将高维数据映射到低维空间中表示，并期望在所投影的维度上数据方差最大，以此使用较少的数据维度，同时保留住较多的原数据点的特性。

PCA本质是借助正交变换方法，将其分量相关的随机向量转化为其分量不相关的新随机向量：

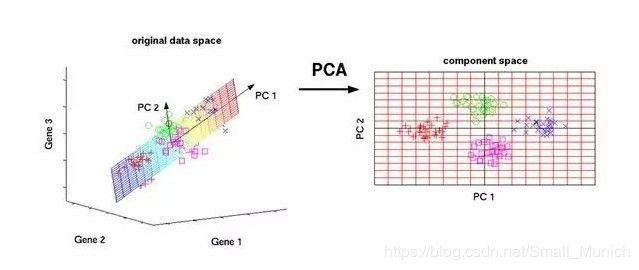
　　其实，从上图可以看出：PCA降维就是通过一种投影映射关系将其数据特征冗余最大程度消除，同时数据特征之间的相关性较低，比较容易区分开来。

PCA算法计算步骤

输入：样本集合$X=\{x_1,x_2,...,x_m\}$

1. 对所有样本的相同维度进行中心化(去均值)：$x_i\leftarrow x_i-\frac{1}{m}{\sum }_i^m{x}_i$

2.计算样本的协方差矩阵$C=\frac{1}{m-1}S\ast S^T$

　　其中$S$为$X$去均值后的矩阵；

3. 对协方差矩阵$C$做特征分解，求取特征值$\lambda =\{{\lambda }_1,{\lambda }_2,...,{\lambda }_m\}$与特征向量$W=\{w_1,w_2,...,w_m\}$

4.按照特征值大小排序，取最大的$d$个特征值对应的特征向量$w_1,w_2,...,w_d$

输出：投影矩阵$W=(w_1,w_2,...,w_d)$

PCA算法示例

　　假设样本集合$X$中的每个样本为二维平面坐标点，其中$x_1=(1,1)$、$x_2=(1,3)$、$x_3=(2,3)$、$x_4=(4,4)$、$x_5=(2,4)$，那么样本集合：
$$X=\left(\begin{array}{ccccc}1& 1& 2& 4& 2\\ 1& 3& 3& 4& 4\end{array}\right)$$

参数解释：
　　其中集合矩阵$X$第一行为：$\{x_1,x_2,x_3,x_4,x_5\}$在$x$轴维度的数据，$X$的第二行为：$\{x_1,x_2,x_3,x_4,x_5\}$在$y$轴维度的数据。

解：

1. 对样本集合X进行中心化，得到矩阵S：

样本集合$X=\{x_1,x_2,x_3,x_4,x_5\}$在$x$轴维度的数据均值为：

$$\overline{x}=\frac{1}{m}\sum _{i=1}^m{x}_i=\frac{1}{5}(1+1+2+4+2)=2$$

样本集合$X=\{x_1,x_2,x_3,x_4,x_5\}$在$y$轴维度的数据均值为：

$$\overline{y}=\frac{1}{m}\sum _{i=1}^m{y}_i=\frac{1}{5}(1+3+3+4+4)=3$$

因此样本集合$X$的第一行每一个元素减去均值$\overline{x}$，第二行的每一个元素减去均值$\overline{y}$，得到矩阵$S$.

$$S=\left(\begin{array}{ccccc}-1& -1& 0& 2& 0\\ -2& 0& 0& 1& 1\end{array}\right)$$

2. 样本的协方差矩阵$C=\frac{1}{m-1}S\ast S^T$

$$\begin{array}{rl}C=& \frac{1}{m-1}S\ast S^T\\ =& \frac{1}{4}\ast \left(\begin{array}{ccccc}-1& -1& 0& 2& 0\\ -2& 0& 0& 1& 1\end{array}\right)\ast \left(\begin{array}{ccccc}-1& -1& 0& 2& 0\\ -2& 0& 0& 1& 1\end{array}\right)\\ =& \left(\begin{array}{cc}1.5& 1\\ 1& 1.5\end{array}\right)\end{array}$$

3.对协方差矩阵$C$做特征分解，求出特征值与特征向量：

特征值为：${\lambda }_1=0.5$，${\lambda }_2=2.5$

其中，特征值${\lambda }_1$与${\lambda }_2$对应的特征向量为：

$$w_1=\left(\begin{array}{c}\frac{-1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right),w_2=\left(\begin{array}{c}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right)$$

协方差矩阵$C$特征值详细求解过程：

$$C=\left(\begin{array}{cc}1.5& 1\\ 1& 1.5\end{array}\right)\text{\hspace{1em}(1)}$$
特征值求取如下：
$$\begin{array}{rl}f(\lambda )=& |\lambda E-C|\\ =& \left|\begin{array}{cc}\lambda -1.5& -1\\ -1& \lambda -1.5\end{array}\right|\\ =& (\lambda -1.5{)}^2-1=0\end{array}\text{\hspace{1em}(2)}$$
则可以得出$\lambda$的值为：${\lambda }_1=0.5$，${\lambda }_2=2.5$.

计算特征值对应的特征向量$w_1$，$w_2$：

$$w_i=\left(\begin{array}{c}{\beta }_1\\ {\beta }_2\end{array}\right)\text{\hspace{1em}(i=1或2)}$$

根据特征向量垂直于$|\lambda E-C|$，则可以得到：

$$|\lambda E-C|\ast w_i=0$$

则，我们可以得到：

$$(\lambda -1.5)\ast {\beta }_1-{\beta }_2=0$$

$${\beta }_1^2+{\beta }_2^2=1$$

当$\lambda =0.5$时候，${\beta }_1=\frac{-1}{\sqrt{2}}$，${\beta }_2=\frac{1}{\sqrt{2}}$，因此：

$$w_1=\left(\begin{array}{c}\frac{-1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right)$$

同理，$w_2$计算为当特征值$\lambda =2.5$的时候：

$$w_2=\left(\begin{array}{c}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right)$$

至此，特征值与特征向量求解结束。

4.特征值$\lambda$按照从大到小排序，对应的特征向量组合成投影矩阵：

投影成一维，我们去${\lambda }_2=2.5$的特征向量

$$W=w_2$$

最后，投影输出$Y=W^{T}C$：

$$\begin{array}{rl}Y=& W^{T}X\\ =& (\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})\ast \left(\begin{array}{ccccc}-1& -1& 0& 2& 0\\ -2& 0& 0& 1& 1\end{array}\right)\\ =& (\frac{-3}{\sqrt{2}},\frac{-1}{\sqrt{2}},0,\frac{3}{\sqrt{2}},\frac{-1}{\sqrt{2}})\end{array}$$

至此，PCA降维整个计算过程就结束啦：$Y$即为样本集合$X$投影后的降维输出。

下面通过坐标变换示意图显示PCA投影过程：

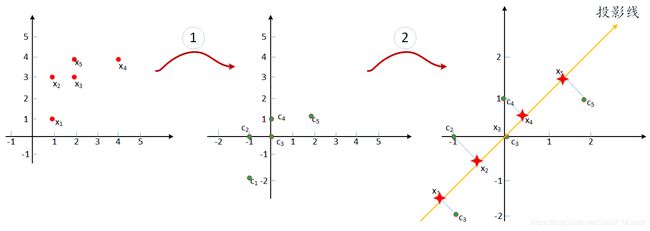
　　上图中，①表示样本集合$X$中的每个样本$x_i$坐标去中心化为第二个坐标轴上面的$c_i$;然后过程②对$c_i$构成的矩阵求出一维投影线，第三个坐标系中的$x_i$就是投影后的坐标表示。

　　举例：第一个坐标系中$x_1=(1,1)$，经过PCA投影降维后$x_1=\frac{-3}{\sqrt{2}}$，维度从两个坐标编程一个坐标进行表示，因此降低维度。

总结

　　本篇博客只是简单介绍一下降维算法PCA的原理及其推导过程，当然PCA算法应用过程中还有许多细节需要考虑。例如：PCA算法中K维度的参数选择？为什么PCA需要求解协方差进行投影降维？PCA算法的优缺点等等。后续将会进行进一步的分析。如果只是将PCA用在维度降低应用下，SVD奇异值分解可以理解为基础的维度降低算法，PCA算是SVD的一种特例。关于SVD是如何进行分解的，可以参考我的另外一篇博文，算法学习之SVD理论推导。最后，如有错误，还请批评指正！

参考文献

李航等 <统计学习方法>
https://blog.csdn.net/shizhixin/article/details/51181379