[笔记]朴素贝叶斯·神经网络·SVM

朴素贝叶斯

在上一讲中的特征 xi 只能取0，1，二元值；一般化的朴素贝叶斯算法中，特征 xi 能取 {1,2,...,ki} 。
这样在对 p(x|y) 进行建模时，就要使用多项式分布，而不是伯努利分布。如果特征是连续值，那么就需要将其离散化，离散到有限的k个值。
例子：居住面积

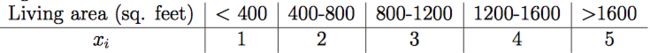
当原始的连续值在多项分布中建模效果不是很好时，离散这些特征然后使用朴素贝叶斯（代替GDA）常常会得到一个更好的结果。

文本分类问题

在特殊语境下的文本分类，朴素贝叶斯使用多元伯努利事件模型(multi-variate Bernoulli event model)。例如上一讲中提到的垃圾邮件分类就采用这个模型。
下面介绍一种不同的模型，多项式事件模型(multinomial event model)。
把一封邮件写成一组特征向量， {x(i)1,x(i)2,...,x(i)n} 。
其中，n为第i封邮件中词的数量；
x表示对应词典中每一个词的索引， x∈{1,2,...,|V|} ，|V|表示词典的大小。
在多项式事件模型中，我们假设一封邮件的产生是一个从一开始就断定(按照 p(y) )是否为垃圾邮件的随机过程。然后，发送者写的第一个词x1服从多项式分布( p(x1|y) )，x2是独立与x1的并且服从同样的多项式分布，x3，x4亦然。所以一封邮件总体的概率为 p(y)∏ni=1p(xi|y) 。需要注意的是，这里 p(xi|y) 是多项式分布，而不是伯努利分布。
模型的参数：

注意 p(xj|y) 对所有的j来说都是一样的，即词的产生和它的位置无关。
数据似然性：

参数的极大似然估计：

总体地含义为，在垃圾邮件的任意位置，下一个位置生成k词的概率。
应用Laplace平滑，分子加1，分母加|V|：

---

神经网络

非线性分类器(Non-linear classifiers)

之前学习的Logistic回归分类算法属于线性分类，通过一条直线将数据分开。但是实际情况中，经常会有数据间的分界并不是直线的，我们希望得到更加匹配数据边界的分类方式。
为了得到非线性分界线的假设，我们可以将特征先输入到多个sigmoid单元，再从这些单元输入到下一级的sigmoid单元。这样就一步步得到了神经网络，其中中间的节点叫做隐藏层，神经网络可以有多个隐藏层。

中间节点的a1、a2、a3可以是：

a1=g(xTθ(1)),g(z)=11+e−z

…最终输出：

hθ(x)=g(a⃗ Tθ(4))

其中θ表示各自的参数； a⃗ T 表示a1、a2、a3组成的向量。
梯队下降算法在神经网络上的应用称为 反向传播算法。
神经网络在面对很强噪音时也能具有很好地性能。

---

支持向量机(SVM)

边界：直观的解释

考虑Logistic回归，通过 hθ(x)=g(θTx) 建模来求得 p(y=1|x;θ) 。
那么，当我们预测“1“时，当且仅当 hθ(x)>0.5 或当且仅当 θTx>=0 。
θTx 越大， hθ(x)=p(y=1|x;w,b) 就越大，就越大程度地预测1。所以如果 θTx≫0 ，y=1；如果 θTx≪0 ，y=0。
也就是说，如果能够找到参数θ使得 θTx(i)≫0 ， y(i)=1 ；并且 θTx(i)≪0 ， y(i)=0 。那么这个分类对训练集是正确的并且确定的。

符号改动

为了方便地讨论SVM，更新：

y∈{−1,+1},输出h∈{−1,+1}

hw,b(x)=g(wTx+b)

其中， z>=0 ， g(z)=1 ； z<0 ， g(z)=−1 。
b(实数)代替了线性分类器中的 θ0 ；w代替了 [θ1,...,θn]T 。

函数间隔

由(w,b)确定的超平面和一个训练样本的函数间隔(functional margin)：

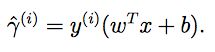
为了使函数间隔很大，如果 y(i)=1 ，那么 wTx+b≫0 ；如果 y(i)=−1 ，那么 wTx+b≪0 。由式子可得出，如果 y(i)(wTx+b)>0 ，那么我们的预测是正确的。
对于整个训练集合，函数间隔定义为：

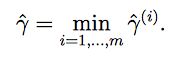
为了得到尽可能大的函数间隔，我们发现将(w,b)变为原来的两倍(2w,2b)可以将函数间隔变大，但是这没有什么意义。所以我们需要引入正则化(normalization)条件来规范表达式，即||w||=1。
那么可以用(w/||w||,b/||w||)替代(w,b)。

几何间隔

w是垂直分隔超平面的，w/||w||是单位向量(unit-length vector)。
对于训练样本A，线段AB的长度表示几何间隔。
那么点B为，
又因为 wTx+b=0 ，所以得到：

解得：

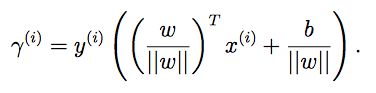
如果||w||=1，那么几何间隔等于函数间隔；
一般来说，几何间隔 = 函数间隔 / ||w||。
几何间隔是不会随着参数的调整「(w,b)->(2w,2b)」而发生变化。
定义整个训练集的几何间隔为单个训练样本的几何间隔的最小值：

最大几何间隔(maximum geometric margin)：