Zcash - 深入浅出Pedersen Hash/Commitment计算

接触过Zcash的人一定都听说过Pedersen Hash，或者Pedersen Commitment。实际上，在Zcash中存在下面4种不同的概念：
1.Pedersen Hash
2.Mixing Pedersen Hash
3.Windowed Pedersen Commitment
4.Homomorphic Pedersen Commitment
你能分清楚它们直接的区别和联系吗？本文将带你一探究竟。

要搞清楚这几个概念，首先需要了解2个术语：Group Hash和Hash Extractor。

1.Group Hash

Group Hash，字面翻译是“群哈希”，但实际的运算是“先做哈希，然后映射到群上”。我们知道，椭圆曲线也是一种加法群，在Zcash中这个“群”指的是Jubjub椭圆曲线。因此，Group Hash实际上是把一个哈希值映射到了椭圆曲线上的一个点，具体流程参考下图：

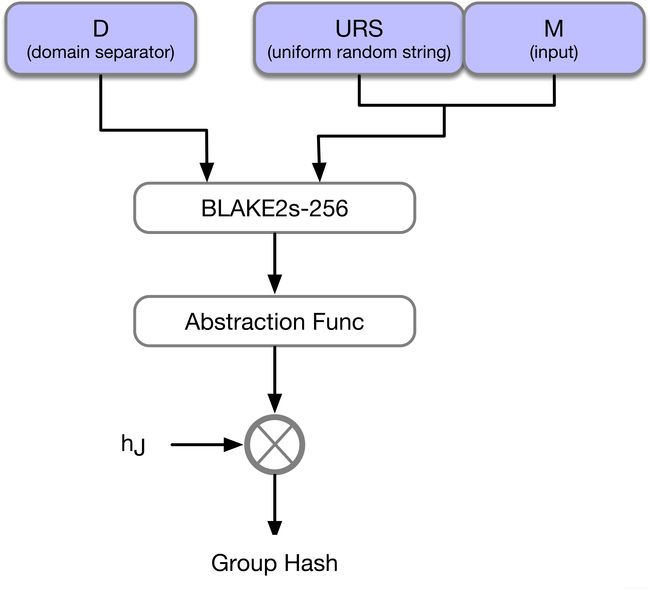
D代表Domain Separator，是一个8字节的字符串，比如“Zcash_PH”。
URS代表Uniform Random String，是一个64字节的均匀随机字符串，在Zcash中的值是：
096b36a5804bfacef1691e173c366a47ff5ba84a44f26ddd7e8d9f79d5b42df0
这个值是用比特币514200高度的区块哈希值，再计算$2^{42}$次SHA-256得到的，也被称为“Randomness Beacon”。
M代表input，可以指定为任意数据。

接下来，对这3个数据做一次BLAKE2s-256哈希。BLAKE2s-256是一个比SHA-256更高效的哈希算法，输出256 bits的结果。

然后将计算出来的哈希值传给Abstraction函数。什么叫做Abstraction函数？实际上，还有一个和它相对的逆运算，叫做Representation函数。我们来看一下Zcash中Representation函数的定义：

其中(u,v)代表椭圆曲线上的点的坐标，所以实际的操作就是：保留y坐标，如果x坐标是奇数的话，最高位（bit 255）置1。
理解了Representation函数，Abstraction函数就是它的逆运算：解出y坐标，带入椭圆曲线求出x坐标，从而恢复出（u,v）。

因此，经过Abstraction函数的处理后，我们就得到了椭圆曲线上的一个点。最后一步是乘上一个系数hJ（默认值是8），就可以获得Group Hash了。

2.Hash Extractor

Hash Extractor，有些地方也叫“Randomness Extractor”，字面翻译是“哈希抽取器”。
我们都知道随机数的重要性，系统中很多地方都需要用到随机数。并且，我们希望获得的是“均匀分布（uniform distribution）”的随机数，但是在实际生活中，我们经常只能从随机源获得“偏置分布（biased distribution）”的随机数。比如我们想随机生成（1,2,3）中的一个数，肯定希望生成3个数的概率是均等的，而不希望生成2的概率比生成1和3的概率要大很多。
Hash Extractor的作用就是：把一个”偏置分布“的随机数转化为一个接近”均匀分布“的随机数。
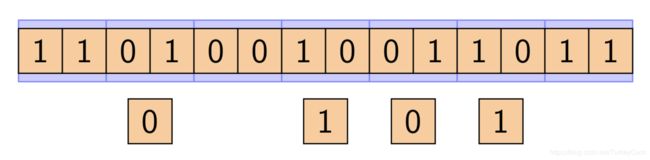
我们以最简单的“冯•诺伊曼Extractor”为例，它的“抽取”规则为：

• 00：不输出
• 11：不输出
• 01：输出0
• 10：输出1

具体示例参见下图：

那么Zcash中的Hash Extractor是如何定义的呢？参见下面的定义：

可以发现，其实很简单，就是只抽取椭圆曲线上点的x坐标。

理解了Group Hash和Hash Extractor，我们就可以开始介绍前面提到的4个概念了。

3.Pedersen Hash

Pedersen Hash的计算流程参见下图：

下面具体分析各个步骤：
1.利用字符串D和数字(0,1,2,…,63)作为输入，生成64个Group Hash：（G0,G1,…,G63）
2.判断输入数据M的bit个数是否是3的倍数，如果不是则进行补零，生成M’
3.将M’划分成n个segment，每个segment的长度是189 bits（3 * 63）
4.将每个segment划分成63个chunk，每个chunk的长度是3 bits
5.每个chunk会通过一个enc()函数进行处理，假设chunk的3个bit分别为(s0,s1,s2)，enc()函数的定义如下：

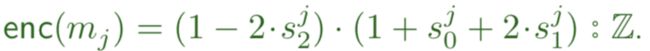
6.将每个chunk处理完的结果分别乘以2^(4i)（i代表当前chunk的索引号），然后将所有结果求和
7.将上一步的结果乘以第1步中生成的Gi（i代表当前segment的索引号），得到当前segment的处理结果
8.将所有segment的处理结果求和，得到Pedersen Hash Point（椭圆曲线上的一个点）
9.将上一步的结果送入Hash Extractor，得到最终的Pedersen Hash

在Zcash中，Pedersen Hash主要用于计算Merkle树的哈希。

4.Windowed Pedersen Commitment

接下来我们来介绍Windowed Pedersen Commitment，在白皮书中有时候也简称为Pedersen Commitment。
还记得上一节提到的Pedersen Hash Point吗？实际上，所谓的Windowed Pedersen Commitment，就是用Pedersen Hash Point再加上椭圆曲线上的一个随机点。这个随机点是通过一个随机数乘上一个Group Hash生成的，具体流程参见下图：

在Zcash中，Windowed Pedersen Commitment主要用于生成Note Commitment。

5.Mixing Pedersen Hash

Mixing Pedersen Hash是在Windowed Pedersen Commitment的基础上，再加上一个椭圆曲线上的随机点。这个随机点是通过一个输入参数x乘上一个Group Hash生成的，生成Group Hash的参数和上一节略有不同。具体流程参见下图：

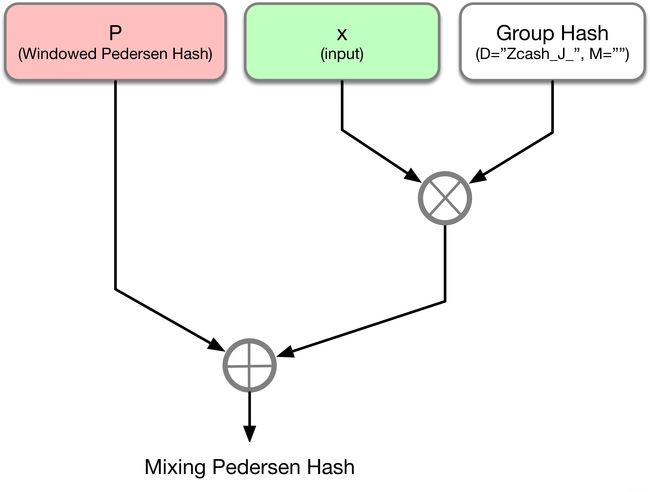
在Zcash中，Mixing Pedersen Hash主要用于计算生成Nullifier的一个参数。

6.Homomorphic Pedersen Commitment

Homomorphic的含义是“同态”，所谓同态，指的是你可以用你“不知道的数”进行运算。
举个例子，假如你有10块钱，需要转给别人7块，找零3块。但是，你想隐藏所有的交易金额，也就是你不想把这3个数字透露给别人。最简单的办法就是用SHA-256算出这3个数字的哈希，然后只发送它们的哈希值：
x = SHA256(amount)
但是由于哈希是确定性的，如果有居心叵测的人把所有可能的金额的哈希都算出来，制成一张表，然后比对哈希值就能猜出对应的金额了。那怎么办呢？我们可以给金额乘上一个随机数，然后再取哈希：
x = SHA256(r * amount)
这个随机数被称为trapdoor，有的论文里也称为“盲因子”。
现在金额被完美隐藏了，但是，当别人收到这3个哈希值以后，怎么验证收入和支出是否平衡（7+3=10）呢？显然，使用这种方法，验证者无法使用你“不知道的数”进行运算，所以SHA-256不满足同态的要求。
因此，我们需要引入一个“同态隐藏函数”的概念。同态隐藏函数commit()需要满足下面3个要求：
1.已知commit(x)，无法反推出x，也就是单向性
2.如果x != y，那么commit(x) != commit(y)，也就是说这是一个单射，或者叫一一映射
3.如果知道了commit(x)和commit(y)，可以计算出commit(x+y)，这样我们就可以用“不知道的数”进行运算了
也就是说，如果我们要验证x = y + z，只需要验证：
commit(r1, x) = commit(r2, y) + commit(r3, z)
在Zcash中，commit()函数是用下面的方式构造的：

其中v就是金额，rcv是一个随机数，它们各自乘上一个椭圆曲线上的点，然后求和，就可以生成Homomorphic Pedersen Commitment。

在Zcash中，Homomorphic Pedersen Commitment主要用于生成Value Commitment，验证输入和输出金额是否一致。

至此，Zcash中涉及的所有Pedersen Hash / Commitment就都介绍完了，欢迎一起交流讨论～

更多文章欢迎关注“鑫鑫点灯”专栏：https://blog.csdn.net/turkeycock
或关注飞久微信公众号：