Zcash - 各种密钥和签名，你懂吗？
Zcash的发展大体经过了OverWinter(过冬) -> Sprout(发芽) -> Sapling(树苗)这几个阶段，随着业务和功能的逐渐丰富，密钥系统也越来越复杂，刚开始接触时感觉一头雾水，但是静下心来仔细分析，就能逐渐领略其中的魅力。
Zcash中的各种密钥，主要是为了实现下面2类功能：
1.Signature
2.In-band secret distribution
签名很好理解，主要是为了保证数据的不可篡改性。那么什么是in-band secret distribution呢？我们知道，Zcash使用了零知识证明，因此交易内部的私密信息对外是隐藏的。但是，如果我想要消费某一笔交易的输出（Note），就必须提供这些私密信息（用于生成Nullifier）。问题来了，交易发送方如何把这些私密信息传递给交易接收方呢？有2种方案：
1.Out-band secret distribution：其实就是“线下”传递，通过一些加密的P2P即时通信工具，比如以太坊的whisper。这种方案比较简单，但是也存在一些缺点，比如要求交易双方必须同时在线，否则就必须引入一些消息持久化方案比如mail server等等。
2.In-band secret distribution：即“线上”传递，也是Zcash目前采用的方案。线上传递的意思是把这些私密信息加密后直接放到交易中上链，接收方再通过某种方式解密以获得私密信息。
下面就逐一介绍一下Sprout和Sapling中的密钥系统，以及在签名及In-band secret distribution中的应用。
1.Sprout
1.1 Sprout密钥系统
Sprout的密钥系统比较简单，参见下图：
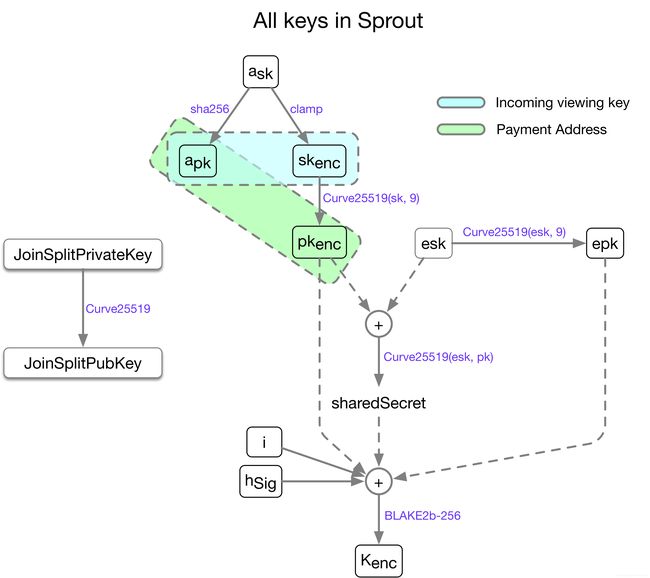
其中Payment Address是发送方需要用到的，Incoming viewing key是给接收方用的。
下面会逐一介绍图上的这些密钥的含义，如果你觉得枯燥难懂，可以先跳过，等看完“签名”和“带内秘密分发”之后再回过头来看这段描述，相信会有不一样的体会。
1. a s k a_{sk} ask：Spending Key，用于生成Nullifier
2. a p k a_{pk} apk：Paying Key，用于生成Note
3.sk_{enc}$：Receiving Key，和epk一起生成sharedSecret，进而生成对称密钥，解密所有的Note Plaintext
s h a r e d S e c r e t = C u r v e 25519 ( s k e n c , e p k ) = s k e n c ⋅ e p k = s k e n c ⋅ e s k ⋅ G sharedSecret=Curve25519(sk_{enc},epk)=sk_{enc} \cdot epk=sk_{enc} \cdot esk \cdot G sharedSecret=Curve25519(skenc,epk)=skenc⋅epk=skenc⋅esk⋅G
4. p k e n c pk_{enc} pkenc：Transmission Key，和esk一起生成sharedSecret，进而生成对称密钥，加密所有的Note Plaintext
s h a r e d S e c r e t = C u r v e 25519 ( e s k , p k e n c ) = e s k ⋅ p k e n c = e s k ⋅ s k e n c ⋅ G sharedSecret=Curve25519(esk,pk_{enc})=esk \cdot pk_{enc}=esk \cdot sk_{enc} \cdot G sharedSecret=Curve25519(esk,pkenc)=esk⋅pkenc=esk⋅skenc⋅G
可以发现，和第3项生成的sharedSecret是完全相同的
5.esk：Ephemeral Secret Key，一个临时私钥，为了生成对称密钥
6.epk：Ephemeral Public Key，一个临时公钥，为了生成对称密钥，包含在JoinSplit中
7. K e n c K_{enc} Kenc：用于加密Note Plaintext的对称密钥，通过KDF生成（5个参数的BLAKE2b-256哈希）
8.JoinSplitPrivateKey：用于对transaction签名
9.JoinSplitPubKey：用于验证transaction签名，包含在transaction中
1.2 Sprout中的JoinSplit Signature
Sprout中只有一种签名，叫做JoinSplit Signature，不过不要被它的名字迷惑了，实际上它是整个transaction的签名：
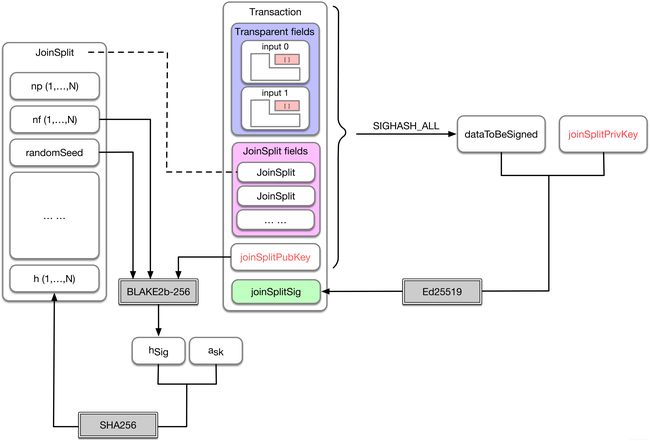
首先看一下签名使用的密钥对：
joinSplitPrivKey是一个随机生成的私钥，joinSplitPubKey则是把Curve25519上对应的公钥，公钥是包含在transaction中的。
之所以使用随机生成的密钥对，目的是为了隐藏用户的身份，因为每次付款都可以生成不同的公钥。
接下来看一下签名使用的输入数据：
输入数据是整个transaction的SIGHASH_ALL类型的哈希。接触过比特币的朋友可能会比较熟悉，比特币解锁脚本中的签名就使用了这种哈希函数。具体来说，就是去除每个input中解锁脚本字段，然后再计算整个交易的哈希。具体细节参考下面的链接：
https://github.com/libbitcoin/libbitcoin-system/wiki/Sighash-and-TX-Signing
Zcash既支持类似比特币的透明交易（transparent transaction），又支持隐私交易（shielded transaction），因此它扩展了比特币原有的交易结构，增加了一些特有字段。在计算哈希时，需要把这些字段也包含进去。
有了密钥对和输入数据，就可以创建签名了，Sprout中使用的是Ed25519签名算法（增加了2个限制条件）。
这里还有一个非常精妙的设计，不得不提一下：
不管是Sprout使用的BCTV14算法，还是Sapling使用的Groth16算法，都存在“Malleability”问题。Malleability可以翻译成“变形”或者“重塑”，指的是可以用已有的proof生成新的合法proof。
因此，我们必须增加一个签名，用来保证数据不被篡改。但是，签名使用的密钥对是随机生成的，那么当别人收到你的交易后，是不是可以把签名和公钥字段去掉，然后自己生成新的密钥对重新签名？为了解决这个问题，我们把所有Nullifier、joinSplitPubKey还有一个randomSeed组合在一起，计算出一个哈希值hSig，然后再把每个Nullifier的私钥ask跟hSig组合在一起，生成N个哈希值并放进JoinSplit中。经过这一波操作，输入数据就跟所有的私钥还有签名者的公钥绑定在了一起，第三方用户就无法替换签名了。用Zcash白皮书中的话来说，这样就保证了“所有ask的持有者都授权了签名交易的人”。
1.3 Sprout in-band secret distribution
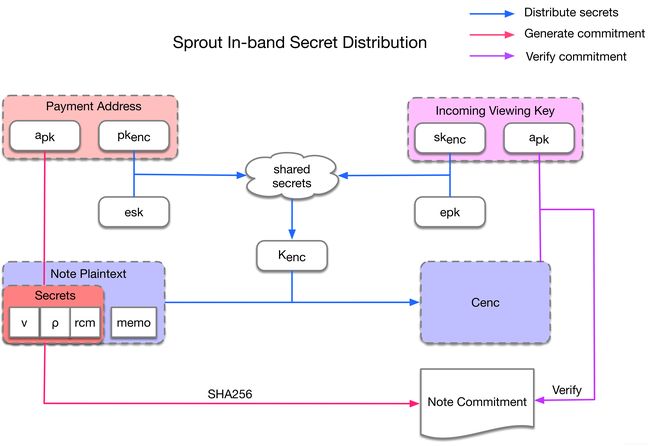图中红色虚线框内是需要传输的秘密，包含3个数据。Note Plaintext中包含这个秘密，同时还包含一个memo字符串。我们目标是安全地把Note Plaintext发送给交易接收方。 首先看蓝线部分： 1.交易发送方拿到接收方的Payment Address，其中包含2个密钥：$a_{pk},pk_{enc}$ 2.然后，随机生成一个临时密钥对esk/epk 3.利用$pk_{enc}$和esk生成一个sharedSecret，然后通过KDF生成对称密钥$K_{enc}$ 4.利用对称密钥对Note Plaintext加密生成$C^{enc}$数据，和epk一起放入交易的JoinSplit中 5.接收方从交易的JoinSplit中拿到epk，和$sk_{enc}$一起生成sharedSecret，然后通过KDF生成对称密钥$K_{enc}$（为什么可以生成相同的sharedSecret？参见1.1节的证明） 6.接收方用$K_{enc}$解密$C^{enc}$，获得秘密
接下来看红线部分：
为了保证数据的正确性，发送方会把秘密和 a p k a_{pk} apk一起生成一个哈希值，称为Note Commitment，放入交易的JoinSplit中，供接收方验证。
最后看紫线部分：
接收方解出秘密，和 a p k a_{pk} apk一起生成哈希值，比对Note Commitment看是否一致。
2.Sapling
2.1 Sapling密钥系统
Sapling的密钥系统采用了分层结构，比Sprout要复杂很多：
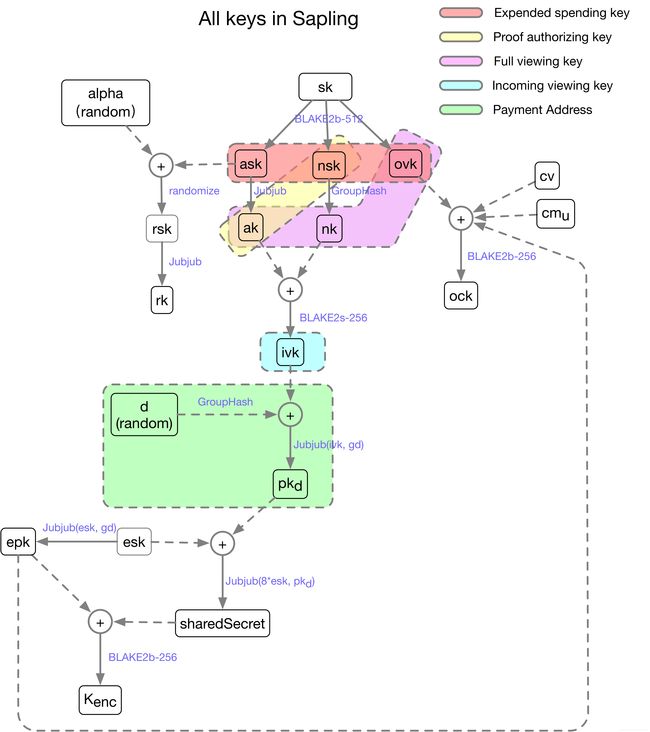
可以发现，更多地使用了随机化，从而减小了公钥暴露账户信息的风险。
首先，不是直接使用Spending Key(sk)，而是派生出了3个Expended Spending Key。
Payment Address也不再是固定值，而是通过一个随机数d和Incoming Viewing Key映射到椭圆曲线上，可以随意生成，从而实现了地址的“多样化（Diversified）”。
另外，除了Incoming Viewing Key，还增加一个Full Viewing Key，不仅可以查看接收到的“Incoming”交易的信息，还可以查看对方发送的“Outgoing”交易的信息。
Proof Authorizing Key会作为零知识证明的auxiliary输入，参与证明的生成。
下面会逐一介绍这些密钥的作用，同样，你也可以先跳过这些内容，等看完了后面的使用场景再来回顾：
1.sk：Spending Key
2.ask：Spend Authorizing Key，通过randomize生成rsk
3.rsk：Randomized ask，由ask生成，用于给SpendDescription签名
4.rk：由rsk生成，用于验证SpendDescription签名
5.nsk：Spend Nullifier Key，作为Proof Authorizing Key的一部分，属于prover的一个auxiliary输入
6.nk：Nullifier Deriving Key，由nsk生成，用于生成Nullifier
7.ak：由ask生成，用于和nk一起生成ivk
8.ivk：Incomming Viewing Key，等于 C R H i v k ( r e p r J ( a k ) , n k ) CRH^{ivk}(repr_{\mathbb J}(ak), nk) CRHivk(reprJ(ak),nk)，可以生成多样化的密钥用于加密Note Plaintext
9.d：一个用于生成Diversified Base的随机数
10. p k d pk_d pkd：Diversified Transmission Key，用于实现In-band secret distribution。接收方可以利用ivk恢复出Note Plaintext。和esk一起生成sharedSecret，然后生成对称密钥，进而加密所有的Note Plaintext
s h a r e d S e c r e t = J u b j u b ( h J ⋅ e s k , p k d ) = h J ⋅ e s k ⋅ p k d = h J ⋅ e s k ⋅ i v k ⋅ g d sharedSecret=Jubjub(h_{\mathbb J} \cdot esk, pk_d)=h_{\mathbb J} \cdot esk \cdot pk_d = h_{\mathbb J} \cdot esk \cdot ivk \cdot g_d sharedSecret=Jubjub(hJ⋅esk,pkd)=hJ⋅esk⋅pkd=hJ⋅esk⋅ivk⋅gd
11.esk/epk：临时密钥对，用于生成对称密钥
12. K e n c K_{enc} Kenc：用于加密Note Plaintext的对称密钥，通过KDF生成（2个参数的BLAKE2b-256哈希）
13.ovk：Outgoing Viewing Key，用于生成ock
14.ock：Outgoing Cipher Key，由ovk、epk等参数生成，用于加密 p k d pk_d pkd和esk，生成 C o u t C^{out} Cout
2.2 RedDSA和RedJubjub
Zcash中定义了一种新的签名算法：RedDSA。RedDSA类似于Ed25519，但算法略有不同，具体流程参见下图：
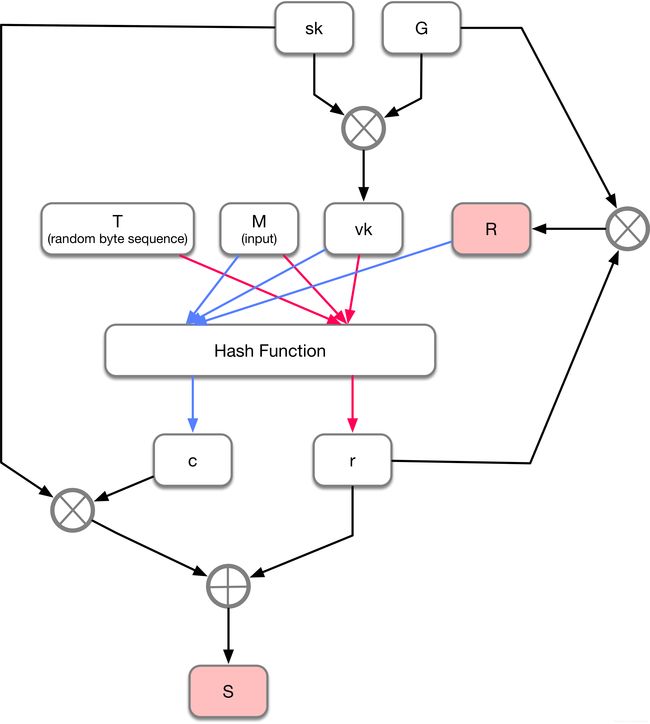
和Ed25519一样，最终的输出是由R和S这2部分拼接起来的。
R是通过把Hash(T,vk,M)的输出映射到椭圆曲线上得到的一个点，最后通过representation function转化为一个标量值。
S则通过计算r+sk•Hash(R,vk,M)得到的的一个标量，结果需要对椭圆曲线的阶次取余。
RedJubjub是RedDSA的一个特化，哈希函数选用BLAKE2b-512，椭圆曲线选用Jubjub。
2.3 Spend Authorization Signature
Sapling中有2种签名，这里先介绍第一种：Spend Authorization Signature。
这个签名的作用是证明你知道 a s k a_{sk} ask，因此你有权花费这边资金。
签名是在整个transaction的SIGHASH_ALL结果之上做的，签名结果放在SpendDescription中。
为了不暴露 a s k a_{sk} ask对应的公钥，采用了re-randomized key的方式（左侧虚线框），通过一个随机数α和一个randomizer生成一个新的私钥rsk，然后再进行RedJubjub签名。为了保证签名和公钥的不可篡改性，α和rk将作为2个auxiluary输入，参与proof的生成。
2.4 Binding Signature
这个签名是为了证明2件事情：
1.shield inputs - shield outputs = transparent value change，也就是隐私交易和透明交易之间的金额必须平衡
2.保证签名者知道生成所有Value Commitment（cv）的随机数（rcv）
签名同样也是在整个transaction的SIGHASH_ALL结果之上做的，签名结果直接放在transaction中。
这个签名有意思的地方在于，签名所使用的密钥对必须通过交易中的数据生成出来，而不是直接记录在交易中的。
我们先来看看私钥bsk，bsk是通过所有SpendDescription中的cv对应的rcv之和，减去所有OutputDescription中的cv对应的rcv之和生成的：
b s k = Σ i = 1 n r c v i o l d − Σ j = 1 m r c v j n e w bsk=\Sigma_{i=1}^n rcv_i^{old}-\Sigma_{j=1}^m rcv_j^{new} bsk=Σi=1nrcviold−Σj=1mrcvjnew
而公钥bvk则是通过SpendDescription中所有cv之和，减去OutputDescription中所有cv之和以及透明交易余额valueBalance的ValueCommit生成的：
b v k = Σ i = 1 n c v i o l d − Σ j = 1 m c v j n e w − V a l u e C o m m i t 0 ( v a l u e B a l a n c e ) bvk=\Sigma_{i=1}^n cv_i^{old}-\Sigma_{j=1}^m cv_j^{new}-ValueCommit_0(valueBalance) bvk=Σi=1ncviold−Σj=1mcvjnew−ValueCommit0(valueBalance)
需要注意的是，生成valueBalance的ValueCommit时，下标为0，表示使用的随机数rcv为0（因为bsk中其实省略了为0的最后一项）。
2.5 In-band Secret Distribution w/ Incoming Viewing Key
Sapling中对密钥进行了更精细的划分，使用Incoming Viewing Key和Full Viewing Key都可以实现In-band Secret Distribution。这里先介绍Incoming View Key的情况：
和Sprout相比，首先Payment Address发生了变化，采用了基于椭圆曲线的“多样化”地址。
蓝线部分和Sprout基本类似：结合临时密钥生成sharedSecret，然后通过KDF生成对称密钥，完成数据传输。
红线部分和Sprout也是相同的，唯一的区别是把SHA256换成了Windowed Pedersen Hash。
紫线部分验证Note Commitment时只需要使用到Payment Address中的公钥，而Payment Address是可以随机生成的，从而最大限度隐藏了用户信息。
2.6 In-band Secret Distribution w/ Full Viewing Key
Sapling中定义了Full Viewing Key的概念，该密钥既可以查看接收方“Incoming”交易的信息，也可以查看发送方”Outgoing“交易的信息，这就是名字中“Full”的由来。
Full Viewing Key包含3个密钥：ovk，ak，nk。
眼尖的朋友可能发现了，有了ak和nk，不就可以生成ivk了吗？所以等价于Full View Key包含了ivk和ovk这2个密钥。这里重点分析一下ovk的作用。
观察上图可以发现，交易中除了包含 C e n c C^{enc} Cenc字段，还增加了一个 C o u t C^{out} Cout字段（绿色部分）。发送方使用ovk和临时密钥epk生成对称密钥ock，然后把用于加密Note Plaintext的2个密钥 p k d pk_d pkd和esk打包到交易中。Full Viewing Key持有者可以以同样的方式生成对称密钥ock，进而解密 C o u t C^{out} Cout，获得这2个密钥。此时他已经获得了发送方生成Outgoing交易的所有信息，可以直接生成对称密钥解开 C e n c C^{enc} Cenc，而不需要借助Incoming Viewing Key了。
3.Zcash是如何实现隐私的
最后，写一点对Zcash实现隐私机制的理解。
所谓隐私，就是要隐藏一笔交易的发送方(from)、接收方(to)、金额(amount)。
1）如何隐藏发送方？
发送方可以随机生成密钥对，然后对交易签名，这样就不会对外暴露固定的公钥。不管是Sprout中的joinSplitSig还是Sapling中的spendAuthSig和bindingSig，都遵循这一原则。
2）如何隐藏接收方？
接收方的Payment Address只有发送方知道，JoinSplit或者OutputDescription中只会提交Note Commitment，因此矿工无法知晓地址该信息，并且也无法在区块链浏览器中查询到。当然，在Sprout中，由于Payment Address是固定的，如果多个发送方串谋，有可能会暴露接收方的信息。因此，在Sapling中引入了“多样化”地址，可以给每个发送方生成不同的地址，从而解决了这个问题。
3）如何隐藏金额？
矿工只需要通过零知识证明验证交易的input和output是平衡的，而不需要查询发送方的余额以及转账金额。
4.总结
Zcash通过引入精细的密钥机制，在实现了交易签名和私密信息分发的前提下，最大限度隐藏了用户信息。
在Sprout中，通过joinSplitSig完美解决了malleability问题，同时采用非对称双密钥的形式实现了In-band secret distribution。
在Sapling中对密钥进一步分层，采用多样化的Payment Address，同时将Spend和Output信息分离并分别签名，在计算能力比较弱的设备上也可以进行简单验证。通过引入Outgoing Viewing Key和Full Viewing Key，更加精细地控制了交易的访问权限。
更多文章欢迎关注“鑫鑫点灯”专栏：https://blog.csdn.net/turkeycock
或关注飞久微信公众号：