遗传算法（Genetic Algorithm ）+C++实现解决TSP问题

概念

生物进化中的概念	遗传算法中的作用
环境	适应函数
适应性	适应函数值
适者生存	适应值大的解被保留的概率大
个体	问题的一个解
染色体	解的编码
基因	编码的元素
群体	被选定的一组解
种群	按适应函数选择的一组解（编码表示）
交配	以一定的方式由双亲产生后代的过程
变异	编码的某些分量发生变化的过程

三个生成过程

• select 自然选择
• crossover 交叉（交配）
• mutation 变异

把每个数据想象成染色体，然后从染色体到人的映射就是object function，也就是这里的适应函数。

当然可以映射到更深的程度，比如考虑人的身高之类的（可以被量化的东西）

• 染色体 这样的比喻，会很容易理解crossover这个步骤。
• 变异这个也很好理解，避免进入到局部极小值，被控制住了。
• 自然选择，这个根据evolutionary theory，也很容易理解

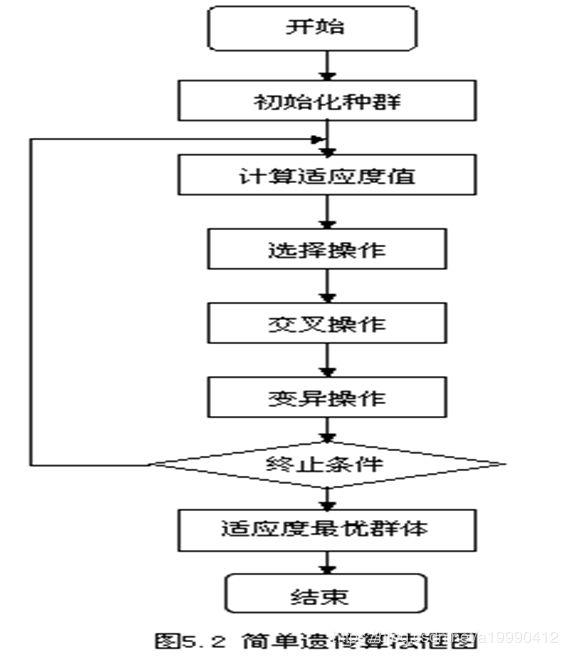
简单遗传算法框架

一般终止条件是：过了很久最优的适应值都不发生变化

整数编码问题

因为如果是二进制编码的话，会简单很多，这里就不讲了。
难点其实还是在整数编码上。

整数编码（简单的实例）：
(有些问题不是排序的问题，就可以类似于之前的二进制来实现)
对于父母分别是 0 到 9整数的排序【加上长度均为10】：
要求子代也必须是这样的排序。

• 自然选择：不会产生子代，只是筛选子代，所以不受这个问题影响
• 交叉（crossover）：会产生子代。这里只考虑排序时候的情况
  • 基于次序的交配法： 在父代1找到几个位置，之后，找到这些数字在父代2的位置。并删除（用空白填充）。之后这些空白按照父代1的中这些数字的顺序排好。（非常简单的方法）
  • 基于位置的交配法： 在父代1找到几个位置，父代2的数值直接替代上去，只会，冲突的位置（不在之前选的位置上冲突的位置），按顺序从父代1替代。
  • 部分映射的交配法： 任意选两个位置，在父代1,2直接这两个位置之间的序列构建序列对。然后，按照这样的序列对的映射方式，在父代1或者父代2上做映射交换。就可以得到子代1或子代2。
• 变异（mutation）：会产生子代。
  • 基于位置的变异： 随机产生两个变异位，然后将第二个变异位上的基因移动到第一个变异位之前。
  • 基于次序的变异： 随机的产生两个变异位，然后交换这两个变异位上的基因。
  • 打乱变异： 随机寻去染色体上的一段，然后打乱在该段内的基因次序。逆序交换方式是打乱变异的一个特例。

TSP问题

TSP，是货郎担问题，也就是中国邮递员问题（少数世界级问问题，用中国人命名的问题hhh）。
就是n个点直接连通需要不同的代价，如果想要找到不重复的经历完所有点，然后在回到初始点的用的代价最小。

用遗传算法解决TSP问题

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

// 随机整数[b, e)
#define RAND(b, e) (rand() % ((e)-(b)) + (b))
// 随机浮点数 0,1
#define RANDFLOAT() ((double)rand() / double(RAND_MAX))

// 种群数量
int LEN = 10;
int tempLEN = 3 * LEN;
// 交配的概率，编译的概率
double pc = 0.8, pm = 0.8;
// 种群的所有路径
int **Paths;
int **tempPaths;
int temp_index = 0;
double **Mat;
double *Value, *tempValue;
int globalValue_index, stay_in_global_times = 0;

double globalValue;
int *globalPath;

// TSP节点数量
int N = 0;

// 适应值函数
double CalValue(int *p) { // read only
	double t = 0;
	for (int i = 1; i < N; ++i) {
		t += Mat[p[i - 1]][p[i]];
	}
	t += Mat[p[N - 1]][0];
	return t;
}

void initialPath(int *Path, int j);
void initialPaths();
void find_min(int first = 1);

// 自然选择
void select();
// 交配
void crossover(int *p1, int* p2);
// 变异
void mutation(int *Path);
//
void preserve(int *p1, int *p2, int v1, int v2);

int main() {
	srand((unsigned)time(NULL));
	ifstream cin("data.txt");

	cin >> N;
	Mat = new double *[N];
	for (int i = 0; i < N; ++i) {
		Mat[i] = new double[N];
	}

	// read data from data.txt
	for (int i = 0; i < N; ++i) {
		for (int j = 0; j < N; ++j) {
			cin >> Mat[i][j];
		}
	}
	// new Path...
	Paths = new int*[LEN];
	for (int i = 0; i < LEN; ++i) {
		Paths[i] = new int[N];
	}
	tempPaths = new int*[tempLEN];
	for (int i = 0; i < tempLEN; ++i) {
		tempPaths[i] = new int[N];
	}
	Value = new double[LEN];
	tempValue = new double[tempLEN];

	globalPath = new int[N];
	// end new Path...
	initialPaths(); // initialize paths

	while (true) {
		temp_index = 0;
		for (int i = 0; i < LEN; i += 2) {
			if (temp_index >= tempLEN) break;
			preserve(Paths[i], Paths[i + 1], Value[i], Value[i + 1]);
			if (temp_index >= tempLEN) break;
			if (RANDFLOAT() < pc) crossover(Paths[i], Paths[i + 1]);
		}

		for (int i = 0; i < LEN; ++i) {
			if (temp_index >= tempLEN) break;
			if (RANDFLOAT() < pm) mutation(Paths[i]);
		}
		select(); 
		if (stay_in_global_times == 1000) { break; }
	}
	cout << globalValue << endl;
	for (int i = 0; i < N; ++i) {
		cout << globalPath[i] << " --> ";
	}

	// delete Path...
	delete[]tempValue;
	delete[]Value;
	for (int i = 0; i < tempLEN; ++i) {
		delete[]tempPaths[i];
	}
	delete[] tempPaths;

	for (int i = 0; i < LEN; ++i) {
		delete[]Paths[i];
	}
	delete[] Paths;

	for (int i = 0; i < N; ++i) {
		delete[] Mat[i];
	}
	delete[]Mat;
	system("pause");
}

// preserve the parents.
void preserve(int *p1, int *p2, int v1, int v2) {
	for (int i = 0; i < N; ++i) {
		tempPaths[temp_index][i] = p1[i];
	}
	tempValue[temp_index] = v1;
	//if (tempValue[temp_index] < 0) cout << "wrong\n";
	temp_index++;
	if (p2 != NULL) {
		for (int i = 0; i < N; ++i) {
			tempPaths[temp_index][i] = p2[i];
		}
		tempValue[temp_index] = v2;
		//if (tempValue[temp_index] < 0) cout << "wrong\n";
		temp_index++;
	}	
}

struct enumate{
	double data;
	int index;
	bool operator < (const enumate& e) const {
		return data < e.data;
	}
};

vector<int> argsort_temp_value() {
	enumate * data = new enumate[temp_index];
	for (int i = 0; i < temp_index; ++i) { 
		data[i].data = tempValue[i];
		data[i].index = i;
	}
	sort(data, data +temp_index);
	vector<int> ans(temp_index);
	for (int i = 0; i < temp_index; ++i) ans[i] = data[i].index;
	delete[]data;
	return ans;
}

void select() {
	vector<int> id = argsort_temp_value();
	for (int i = 0; i < temp_index; ++i) if (tempValue[i] < 0)cout << tempValue[i] << endl;
	for (int i = 0; i < LEN; ++i) {
		Value[i] = tempValue[id[i]];
		for (int j = 0; j < N; ++j) {
			Paths[i][j] = tempPaths[id[i]][j];
		}
	}
	if (Value[0] < globalValue) {
		for (int i = 0; i < N; ++i) globalPath[i] = Paths[0][i];
		stay_in_global_times = 0;
		globalValue = Value[0];
	}
	else if (Value[0] == globalValue) {
		stay_in_global_times++;
	}
	else {
		cout << "Something wrong" << Value[0]<< endl;
	}
}

// 基于次序的交配方式
void crossover(int * p1, int * p2)
{
	// generate son from p1 and p2
	int crossn = RAND(0, N-1);
	if (crossn == 0) return;
	int * indexs = new int[crossn];
	for (int i = 0; i < crossn; ++i) {
		if (i == 0) indexs[i] = RAND(1, N - crossn + 1);
		else { 
			indexs[i] = RAND(indexs[i - 1] + 1, N - crossn + i + 1);
		}
	}
	// copy from p2
	for (int i = 0; i < N; ++i) {
		tempPaths[temp_index][i] = p2[i];
	}
	int use_count = 0;
	for (int i = 0; i < N; ++i) {
		if (use_count == crossn) break;
		for (int j = 0; j < crossn; ++j) {
			if (tempPaths[temp_index][i] == p1[indexs[j]]) {
				tempPaths[temp_index][i] = p1[indexs[use_count]];
				use_count++;
				break;
			}
		}
	}
	// cal value
	tempValue[temp_index] = CalValue(tempPaths[temp_index]);
	
	temp_index++;
	// copy from p1
	for (int i = 0; i < N; ++i) {
		tempPaths[temp_index][i] = p1[i];
	}
	use_count = 0;
	for (int i = 0; i < N; ++i) {
		if (use_count == crossn) break;
		for (int j = 0; j < crossn; ++j) {
			if (tempPaths[temp_index][i] == p2[indexs[j]]) {
				tempPaths[temp_index][i] = p2[indexs[use_count]];
				use_count++;
				break;
			}
		}
	}
	tempValue[temp_index] = CalValue(tempPaths[temp_index]);
	temp_index++;
	delete[] indexs;
}

// 基于次序的变异
void mutation(int * Path)
{
	int a = RAND(1, N), b, t;
	if (a == N - 1) {
		b = RAND(1, N - 1);
		t = a; 
		a = b; 
		b = t;
	}
	else {
		b = RAND(a + 1, N);
	}
	for (int i = 0; i < N; ++i) {
		if (i == a)
			tempPaths[temp_index][i] = Path[b];
		else if ( i == b )
			tempPaths[temp_index][i] = Path[a];
		else tempPaths[temp_index][i] = Path[i];
	}
	tempValue[temp_index] = CalValue(tempPaths[temp_index]);
	temp_index++;
}

void initialPaths() {
	for (int i = 0; i < LEN; ++i)
		initialPath(Paths[i], i);
	find_min();
}

void find_min(int first)
{
	int temp = 0;
	for (int i = 1; i < LEN; ++i)
		if (Value[temp] > Value[i]) temp = i;
	if (first) {
		globalValue = Value[temp];
		for (int i = 0; i < N; ++i)
			globalPath[i] = Paths[temp][i];
	}
	else if (Value[temp] < globalValue) {
		globalValue = Value[temp];
		for (int i = 0; i < N; ++i)
			globalPath[i] = Paths[temp][i];
	}
}

void initialPath(int *Path, int j) {
	for (int i = 0; i < N; ++i) {
		Path[i] = i;
	}
	// Path[i]表示路上第i个点的标记为Path[i]
	// Path[0] = 0
	int tx, t;
	for (int i = 1; i < N - 1; ++i) {
		tx = RAND(i, N);
		if (tx != i) { // swap
			t = Path[i];
			Path[i] = Path[tx];
			Path[tx] = t;
		}
	}
	Value[j] = CalValue(Path);

}

这里用的数据跟之前的用退火算法的结果是一样的。
模拟退火算法理论+Python解决函数极值+C++实现解决TSP问题

• 结果是也是一样的，对于这个，我们可以设置重复多少次来停止来控制这个精度。
• 为了避免到局部最优解，也可以使用提高变异概率来设计。
• 结果是大概率收敛到较好的结果。

244
0 --> 6 --> 2 --> 8 --> 9 --> 7 --> 5 --> 1 --> 3 --> 4 -->

改进版本代码

• 改进点：交配的尝试会在每人之间都相互试试看。提高了随机性，所以会更稳定的收敛到结果。因此就不用太多次的停滞就可以控制住。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

// 随机整数[b, e)
#define RAND(b, e) (rand() % ((e)-(b)) + (b))
// 随机浮点数 0,1
#define RANDFLOAT() ((double)rand() / double(RAND_MAX))

// 种群数量
int LEN = 22;
int tempLEN = LEN * LEN;
// 交配的概率，编译的概率
double pc = 0.8, pm = 0.9;
// 种群的所有路径
int **Paths;
int **tempPaths;
int temp_index = 0;
double **Mat;
double *Value, *tempValue;
int globalValue_index, stay_in_global_times = 0;

double globalValue;
int *globalPath;

// TSP节点数量
int N = 0;

// 适应值函数
double CalValue(int *p) { // read only
	double t = 0;
	for (int i = 1; i < N; ++i) {
		t += Mat[p[i - 1]][p[i]];
	}
	t += Mat[p[N - 1]][0];
	return t;
}

void initialPath(int *Path, int j);
void initialPaths();
void find_min(int first = 1);

// 自然选择
void select();
// 交配
void crossover(int *p1, int* p2);
// 变异
void mutation(int *Path);
//
void preserve(int *p1, int *p2, int v1, int v2);

int main() {
	srand((unsigned)time(NULL));
	ifstream cin("data.txt");

	cin >> N;
	Mat = new double *[N];
	for (int i = 0; i < N; ++i) {
		Mat[i] = new double[N];
	}

	// read data from data.txt
	for (int i = 0; i < N; ++i) {
		for (int j = 0; j < N; ++j) {
			cin >> Mat[i][j];
		}
	}
	// new Path...
	Paths = new int*[LEN];
	for (int i = 0; i < LEN; ++i) {
		Paths[i] = new int[N];
	}
	tempPaths = new int*[tempLEN];
	for (int i = 0; i < tempLEN; ++i) {
		tempPaths[i] = new int[N];
	}
	Value = new double[LEN];
	tempValue = new double[tempLEN];

	globalPath = new int[N];
	// end new Path...
	initialPaths(); // initialize paths

	while (true) {
		temp_index = 0;
		for (int i = 0; i < LEN; i++) {
			if (temp_index >= tempLEN) break;
			preserve(Paths[i], NULL, Value[i], NULL);
			for (int j = i+1; j < LEN; ++j) {
				if (temp_index >= tempLEN) break;
				if (RANDFLOAT() < pc) crossover(Paths[i], Paths[j]);
			}
		}

		for (int i = 0; i < LEN; ++i) {
			if (temp_index >= tempLEN) break;
			if (RANDFLOAT() < pm) mutation(Paths[i]);
		}
		select(); 
		if (stay_in_global_times == 10) { break; }
	}
	cout << globalValue << endl;
	for (int i = 0; i < N; ++i) {
		cout << globalPath[i] << " --> ";
	}

	// delete Path...
	delete[]tempValue;
	delete[]Value;
	for (int i = 0; i < tempLEN; ++i) {
		delete[]tempPaths[i];
	}
	delete[] tempPaths;

	for (int i = 0; i < LEN; ++i) {
		delete[]Paths[i];
	}
	delete[] Paths;

	for (int i = 0; i < N; ++i) {
		delete[] Mat[i];
	}
	delete[]Mat;
	system("pause");
}

// preserve the parents.
void preserve(int *p1, int *p2, int v1, int v2) {
	for (int i = 0; i < N; ++i) {
		tempPaths[temp_index][i] = p1[i];
	}
	tempValue[temp_index] = v1;
	//if (tempValue[temp_index] < 0) cout << "wrong\n";
	temp_index++;
	if (p2 != NULL) {
		for (int i = 0; i < N; ++i) {
			tempPaths[temp_index][i] = p2[i];
		}
		tempValue[temp_index] = v2;
		//if (tempValue[temp_index] < 0) cout << "wrong\n";
		temp_index++;
	}	
}

struct enumate{
	double data;
	int index;
	bool operator < (const enumate& e) const {
		return data < e.data;
	}
};

vector<int> argsort_temp_value() {
	enumate * data = new enumate[temp_index];
	for (int i = 0; i < temp_index; ++i) { 
		data[i].data = tempValue[i];
		data[i].index = i;
	}
	sort(data, data +temp_index);
	vector<int> ans(temp_index);
	for (int i = 0; i < temp_index; ++i) ans[i] = data[i].index;
	delete[]data;
	return ans;
}

void select() {
	vector<int> id = argsort_temp_value();
	for (int i = 0; i < temp_index; ++i) if (tempValue[i] < 0)cout << tempValue[i] << endl;
	for (int i = 0; i < LEN; ++i) {
		Value[i] = tempValue[id[i]];
		for (int j = 0; j < N; ++j) {
			Paths[i][j] = tempPaths[id[i]][j];
		}
	}
	if (Value[0] < globalValue) {
		for (int i = 0; i < N; ++i) globalPath[i] = Paths[0][i];
		stay_in_global_times = 0;
		globalValue = Value[0];
	}
	else if (Value[0] == globalValue) {
		stay_in_global_times++;
	}
	else {
		cout << "Something wrong" << Value[0]<< endl;
	}
}

// 基于次序的交配方式
void crossover(int * p1, int * p2)
{
	// generate son from p1 and p2
	int crossn = RAND(0, N-1);
	if (crossn == 0) return;
	int * indexs = new int[crossn];
	for (int i = 0; i < crossn; ++i) {
		if (i == 0) indexs[i] = RAND(1, N - crossn + 1);
		else { 
			indexs[i] = RAND(indexs[i - 1] + 1, N - crossn + i + 1);
		}
	}
	// copy from p2
	for (int i = 0; i < N; ++i) {
		tempPaths[temp_index][i] = p2[i];
	}
	int use_count = 0;
	for (int i = 0; i < N; ++i) {
		if (use_count == crossn) break;
		for (int j = 0; j < crossn; ++j) {
			if (tempPaths[temp_index][i] == p1[indexs[j]]) {
				tempPaths[temp_index][i] = p1[indexs[use_count]];
				use_count++;
				break;
			}
		}
	}
	// cal value
	tempValue[temp_index] = CalValue(tempPaths[temp_index]);
	
	temp_index++;
	// copy from p1
	for (int i = 0; i < N; ++i) {
		tempPaths[temp_index][i] = p1[i];
	}
	use_count = 0;
	for (int i = 0; i < N; ++i) {
		if (use_count == crossn) break;
		for (int j = 0; j < crossn; ++j) {
			if (tempPaths[temp_index][i] == p2[indexs[j]]) {
				tempPaths[temp_index][i] = p2[indexs[use_count]];
				use_count++;
				break;
			}
		}
	}
	tempValue[temp_index] = CalValue(tempPaths[temp_index]);
	temp_index++;
	delete[] indexs;
}

// 基于次序的变异
void mutation(int * Path)
{
	int a = RAND(1, N), b, t;
	if (a == N - 1) {
		b = RAND(1, N - 1);
		t = a; 
		a = b; 
		b = t;
	}
	else {
		b = RAND(a + 1, N);
	}
	for (int i = 0; i < N; ++i) {
		if (i == a)
			tempPaths[temp_index][i] = Path[b];
		else if ( i == b )
			tempPaths[temp_index][i] = Path[a];
		else tempPaths[temp_index][i] = Path[i];
	}
	tempValue[temp_index] = CalValue(tempPaths[temp_index]);
	temp_index++;
}

void initialPaths() {
	for (int i = 0; i < LEN; ++i)
		initialPath(Paths[i], i);
	find_min();
}

void find_min(int first)
{
	int temp = 0;
	for (int i = 1; i < LEN; ++i)
		if (Value[temp] > Value[i]) temp = i;
	if (first) {
		globalValue = Value[temp];
		for (int i = 0; i < N; ++i)
			globalPath[i] = Paths[temp][i];
	}
	else if (Value[temp] < globalValue) {
		globalValue = Value[temp];
		for (int i = 0; i < N; ++i)
			globalPath[i] = Paths[temp][i];
	}
}

void initialPath(int *Path, int j) {
	for (int i = 0; i < N; ++i) {
		Path[i] = i;
	}
	// Path[i]表示路上第i个点的标记为Path[i]
	// Path[0] = 0
	int tx, t;
	for (int i = 1; i < N - 1; ++i) {
		tx = RAND(i, N);
		if (tx != i) { // swap
			t = Path[i];
			Path[i] = Path[tx];
			Path[tx] = t;
		}
	}
	Value[j] = CalValue(Path);

}