数据分析-回归分析读书笔记

解决三个问题

羽美想预测明天的冰茶销量

宫野想估算在一个新的地址开店的月销售额 

羽美想推测一下明天的特供蛋糕卖出去的可能性

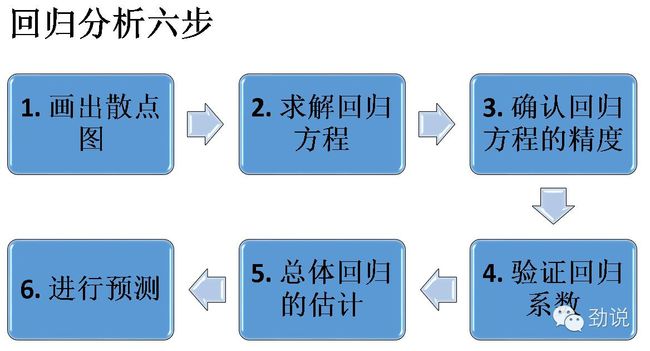
回归分析的基础流程分六步

线性回归

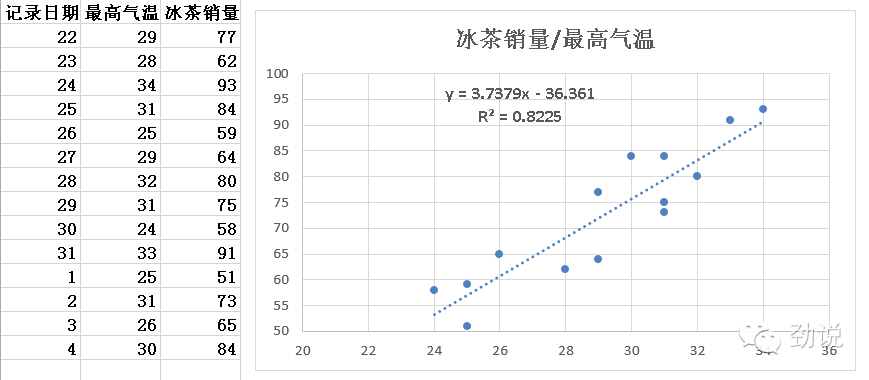
羽美想预测明天的冰茶销量。羽美知道冰茶在天热的时候销量好。记录的店中冰茶的销售数据在下表，先画出散点图观察相关性，下图是明显的正相关

可以通过添加趋势线，勾选显示公式和R平方值，轻松就搞定回归方程和精度估计

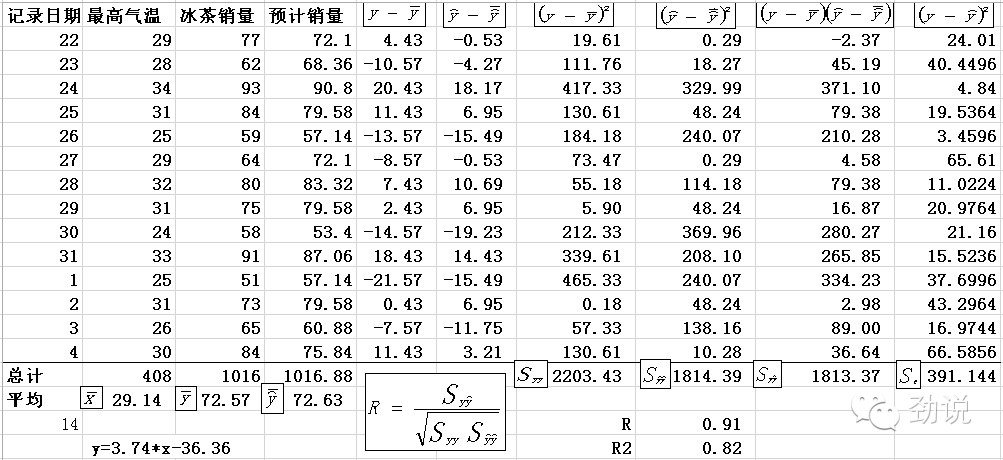
也可以自己用公式来计算，先求x的平均，y的平均，Sxx，Syy，Syy，通用Se的对a，b的微分=0可以推导出a，b的计算公式

用公式计算R平方看看数据和方程的拟合程度，越接近1拟合程度越高

将上面的数据作为抽样数据，可以估算出总体的分布，用F分布检测总体回归系数，计算出的统计量的概率和0.05比较

对总体回归做估值，在置信度为95%时计算置信区间，计算温度在31度时的置信区间

在置信度为95%时候计算预测区间，计算温度在31度时的预测区间，预测区间的取值范围要比估值区间更宽一些

观察个体的标准化残差，当个体的标准化残差的绝对值大于3时，应该剔除后再进行回归分析

使用Durbin-Watson统计量评估序列自相关程度，如果值在2左右，说明不存在序列自相关

可用尝试多种形式的方程做回归，通过观察散点图判断拟合程度比较好的函数，选择回归后的R平方大的函数

多元回归

宫野想估算在一个新的地址开店的月销售额。宫野知道营业面积越大，距离车站越近，店铺的销售额就越大。各家门店的销售数据如下表，首先画出散点图观察相关性，通过Correl函数计算相关系数，一个是0.89，一个是-0.77都相关显著

用Linest函数计算回归系数，注意Linest计算出的系数是反序的，带入系数就有了回归方程，接下来计算Syy、Se，因为多元回归中R的计算会受到自变量个数的影响，就用修正自由度的R2公式

对总体回归检验回归系数和偏回归系数的检测统计量

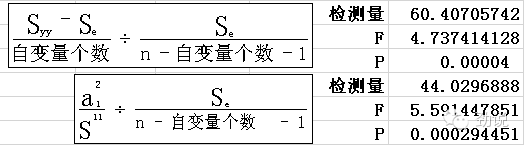
其中用到的S11的求解过程，A的转置用“粘贴”的时候勾选“转置”，矩阵相乘法用MMult函数，矩阵求逆用MInverse函数，S11就是对角线上第一行第一列的元素

计算估值区间和预测区间，多元回归采用马氏距离避免欧式距离的量岗的问题

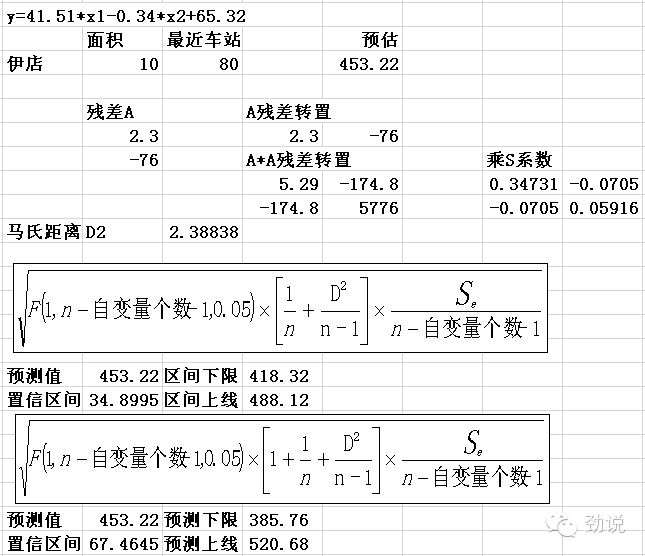
多元回归的自变量可以很多，可以对自变量进行组合，用修正自由度的R平方评估后选择最好的组合

多元回归将分类变量拆分为n-1个变量来处理，比如：性别有男、女和其他，拆分为性别男，性别女二个变量，用1,表示是，0表示否

逻辑回归

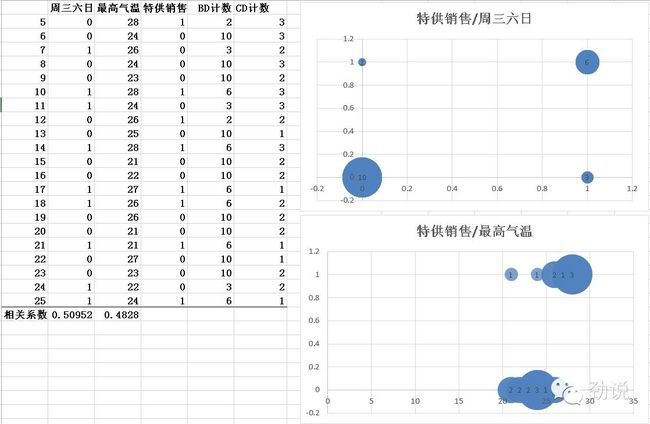
羽美想推测一下明天的特供蛋糕卖出去的可能性。羽美的经验告诉她周三六日客户比较多，好像和温度也有点关系。特供蛋糕的销售数据如下表，首先画出气泡图观察相关性，用气泡是因为点有密集的堆叠，通过Countif辅助列算出气泡的大小，就可以画出气泡吐了，然后用Correl函数计数相关系数

用规划求解完成逻辑回归系数的计算，因为探测计算中可能会出现销售预测的值过小，从而导致对数释然计算的溢出失败，需要调整销售预测函数=1/(1+EXP(-IF(G2>-700,G2,-700)))做最小值的溢出保护，同时要约束系数变量不为零--AND(NOT($B$24=0),NOT($C$24=0),NOT($D$24=0))，注明：--是转换成整数

下面计算R平方的，这里n1,n0分别是样本中卖出去的个数和没有卖出去的个数，逻辑回归中R平方是越小越显著，可以计算误判率，卖出和预测卖出的相关系数观察模型精确程度

总体系数的检测，用x2的2自由度检测

检测偏回归系数，用x2的1自由度检测

预测明天特供蛋糕卖出去的可能性，将明天是否周三六日和明天气温带入方程后得到0.44<0.5，估计是卖不出去了

Excel的相关功能

散点图观察相关性，添加趋势线

气泡图观察点密集情况下的相关性

Exp指数函数 Log对数函数 Ln自然对数函数

Correl相关函数检测二个变量之间的相关性

Linest函数计算线性回顾系数

FDist和FInv是F分布函数和逆函数

ChiDist和ChiInv是X2分布函数和逆函数

MMult、MInverse、Transpose是矩阵的乘法、逆函数、转置函数

规划求解参数绝对是个好东西