最大流算法:Edmond-Karp算法——Ford-Fulkerson算法——Dinic算法
- 问题定义
- 限制条件
- 示例
- 基本思想
- 引入反向边
- Edmond-Karp算法
- Ford-Fulkerson算法
- 使用DFS的Ford-Fulkerson算法
- 递归设计错误示范
- 递归正确设计
- 递归次数优化
- 最大流图的最后抵消
- Dinic算法
- 基本思想
- 设计程序
- 代码实现
- 另一种代码实现
问题定义
给定有向图G=(V,E),其每条边都有容量 cv,w c v , w .这个容量代表这个边可以通过的最大容量。对于任一条边 (v,w) ( v , w ) ,在从v到w的方向上,最多有 cv,w c v , w 个单位的流可以通过。注意容量也是具有方向的。
图中有两个特殊点,一个是s,称为源点(source),一个是t,称为收点(sink)。
既不是源点也不是收点的点,总的进入的流必须等于总的发出的流。
最大流问题就是确定从s到t可以通过的最大流量。
问题对于有环无环并没有要求,所以算法必须也能解决有环的情况。
限制条件
对于任一条边 (v,w) ( v , w ) ,在其上运行的流的流量必须<= cv,w c v , w
对于任一节点,总的进入的流必须等于总的发出的流(除了源点、收点)
示例

如上图所示,左边是为一个图,右边为该图的最大流示意图。
实际左边的图,每条边上的数字既代表了这条边的容量,也代表了这条边的初始流量,但这个初始流量实际上是不能都达到的,因为限制条件(总的进入的流必须等于总的发出的流),所以问题需要我们找到这个图的实际流量到达都是多少,且还要求从s到t通过最大流量。
从上图中好像很容易就发现了最大流为5,因为直接看源点或者收点的总流量就是5.但下面这个图就不能直接看出了。

如上图所示,如果只看源点或者收点,那么你可能会觉得最大流为6,但实际上最大流为5.
左图的虚线切分就证明了该图的最大流为5,直观上来看,虚线切分的两条边加起来的和就为5.
切分要求:将图切分成两部分,一部分包括s和其他一些顶点;另一部分包括t和其他一些顶点。并且切分到的边,比如这里的边 (a,c)(d,t) ( a , c ) ( d , t ) ,要让边的前驱在s分区,边的后继在t分区。这样的切分一般有多种情况,具有最小总容量的切分便是给出最大流。
基本思想
首要想法是分阶段进行。从原图 G G 构造一个流图 Gf G f 。 Gf G f 代表算法在任意阶段已经到达的流。开始时 Gf G f 所有的边都没有流,我们希望算法终止时 Gf G f 包括最大流。
还构造一个图 Gr G r ,称为残余图(residual graph),表示在 Gf G f 上每条边还能再添加上多少流。开始时 Gr G r 就等于原图 G G 。
每当我们对 Gf G f 里面的边添加流时,就会对 Gr G r 里同样的边减小流。
在每个阶段,我们寻找 Gr G r 中从s到t的一条路径,称作增广路径(augmenting path)。增广路径上所有边的最小权值就是可以添加路径上所有边的流的量。我们通过不断减小 Gr G r 的流,增加 Gf G f 的流来执行算法。
当发现在 Gr G r 中没有了从s到t的路径时,算法停止。
但这种思路,有可能会让算法找不到最优解,因为每次选择增广路径不一定都是最好的选择。

如上图,左边为 Gf G f ,右边为 Gr G r 。现在为初始状态。

选择了增广路径为s,b,d,t。一旦消耗光了残余图的某条边的流量,残余图里就需要去掉这条边。

选择了增广路径为s,a,c,t。

最好选择了增广路径为s,a,d,t。算法终止,因为没有路径能从s到t了。
引入反向边
如果上述过程,从初始情况,我们选择路径s,a,d,t,这条路径虽然能有3的最小流量,好像是一种不错的选择。但这样选择后,却让算法直接终止了,因为没有增广路径了。这就表示贪婪算法行不通。失败原因如下图:

为了得到最优解,我们需要能让算法撤销决定,如果我们之前作出了错误决定的话。
所以,在算法的每个阶段,修改残余图时,根据增广路径减小相应的流时(增广路径的流为f),还要对增广路径的每条边 (v,w) ( v , w ) 的反向边 (w,v) ( w , v ) 添加一条容量为f的边。
这样做的效果就是,我们能以相反的方向,再走一遍之前走过的流。即能使算法撤销之前做的决定。
下面的示例说明了反向边的作用。

第一次选择路径s,a,d,t。并且向残余图添加反向边。

第二次选择路径s,b,d,a,c,t。其中从d到a,就走了上一步走的反方向的流,通过这样来让算法反悔决定。没有了增广路径,算法停止。
反向边是算法的精华部分所在,本来第一步时边 (d,a) ( d , a ) 的流为3(这是第一次寻找增广路径产生的反向边),但第二步由于增广路径的选择导致 (d,a) ( d , a ) 的流被抵消掉了2单位的流。
为什么加反向边不会有坏的影响呢,因为它的方向是从t到s的,是反方向的,加了寻找增广路径也不可能出错。但加了以后,却让寻找增广路径有了更多的选择即回退的选择。
回退的意思其实就是,第二次选择的增广路径,可以抵消掉第一次选择的增广路径的流(这里指的最大流图)
Edmond-Karp算法
代码部分参考了网络流—最大流(Edmond-Karp算法)
,用python3进行了实现。
使用的图就是本文第一个图的左边的图。
from queue import Queue
#n #边的个数
m = 6#点的个数
residual = [[0 for i in range(m)] for j in range(m)]
#残余图的剩余流量
maxflowgraph = [[0 for i in range(m)] for j in range(m)]
#记录最大流图,初始都为0
flow = [0 for i in range(m)]
#记录增广路径前进过程记录的最小流量
pre = [float('inf') for i in range(m)]
#记录增广路径每个节点的前驱
q = Queue()
#队列,用于BFS地寻找增广路径
#设置初始图的流量走向
residual[0][1]=3
residual[0][2]=2
residual[1][2]=1
residual[1][3]=3
residual[1][4]=4
residual[2][4]=2
residual[3][5]=2
residual[4][5]=3
def BFS(source,sink):
q.empty()#清空队列
for i in range(m):
pre[i] = float('inf')
flow[source] = float('inf')#这里要是不改,那么找到的路径的流量永远是0
#不用将flow的其他清零
q.put(source)
while(not q.empty()):
index = q.get()
if(index == sink):
break
for i in range(m):
if( (i!=source) & (residual[index][i]>0) & (pre[i]==float('inf')) ):
#i!=source,从source到source不用分析了
#residual[index][i]>0,边上有流量可以走
#pre[i]==float('inf'),代表BFS还没有延伸到这个点上
pre[i] = index
flow[i] = min(flow[index],residual[index][i])
q.put(i)
if(pre[sink] == float('inf')):
#汇点的前驱还是初始值,说明已无增广路径
return -1
else:
return flow[sink]
def maxflow(source,sink):
sumflow = 0#记录最大流,一直累加
augmentflow = 0#当前寻找到的增广路径的最小通过流量
while(True):
augmentflow = BFS(source,sink)
if(augmentflow == -1):
break#返回-1说明已没有增广路径
k = sink
while(k!=source):#k回溯到起点,停止
prev = pre[k]#走的方向是从prev到k
maxflowgraph[prev][k] += augmentflow
residual[prev][k] -= augmentflow#前进方向消耗掉了
residual[k][prev] += augmentflow#反向边
k = prev
sumflow += augmentflow
return sumflow
result = maxflow(0,m-1)
print(result)
print(maxflowgraph)#最大流图BFS函数用来选择增广路径,每当寻找到增广路径时,就对残余图和最大流图作相应的修改。运行结果如下:5代表最大流大小;二维list代表最大流图。
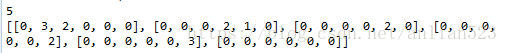
示意图如下:

有环这个算法也能执行,将这行代码residual[1][4]=4改为residual[4][1]=4,此时出现环,从1到2到4的环。运行结果为:

示意图如下:原图中,橙色箭头就是形成的环

Ford-Fulkerson算法
首先附上geeksforgeeks的友情链接Ford-Fulkerson Algorithm for Maximum Flow Problem,虽然是英文的,但讲得挺好的。
The above implementation of Ford Fulkerson Algorithm is called Edmonds-Karp Algorithm. The idea of Edmonds-Karp is to use BFS in Ford Fulkerson implementation as BFS always picks a path with minimum number of edges. When BFS is used, the worst case time complexity can be reduced to O(VE2). The above implementation uses adjacency matrix representation though where BFS takes O(V2) time, the time complexity of the above implementation is O(EV3) (Refer CLRS book for proof of time complexity)
上面这段话来自友情链接。意思就是,Ford-Fulkerson算法其实就是一种思想,不是一种具体的实现。而Edmonds-Karp算法是对Ford-Fulkerson算法的一种实现,实现的特点就在,在选择增广路径时,采用BFS的方法寻找。Ford-Fulkerson算法只是一种思想的原因就在于,它并没有确定下来,寻找增加路径时,到达采用什么方法,比如可以BFS,DFS,贪心等等。
友情链接的python代码如下:
# Python program for implementation of Ford Fulkerson algorithm
from collections import defaultdict
#This class represents a directed graph using adjacency matrix representation
class Graph:
def __init__(self,graph):
self.graph = graph # residual graph
self. ROW = len(graph)
#self.COL = len(gr[0])
'''Returns true if there is a path from source 's' to sink 't' in
residual graph. Also fills parent[] to store the path '''
def BFS(self,s, t, parent):
# Mark all the vertices as not visited
visited =[False]*(self.ROW)
# Create a queue for BFS
queue=[]
# Mark the source node as visited and enqueue it
queue.append(s)
visited[s] = True
# Standard BFS Loop
while queue:
#Dequeue a vertex from queue and print it
u = queue.pop(0)
# Get all adjacent vertices of the dequeued vertex u
# If a adjacent has not been visited, then mark it
# visited and enqueue it
for ind, val in enumerate(self.graph[u]):
if visited[ind] == False and val > 0 :
queue.append(ind)
visited[ind] = True
parent[ind] = u
# If we reached sink in BFS starting from source, then return
# true, else false
return True if visited[t] else False
# Returns tne maximum flow from s to t in the given graph
def FordFulkerson(self, source, sink):
# This array is filled by BFS and to store path
parent = [-1]*(self.ROW)
max_flow = 0 # There is no flow initially
# Augment the flow while there is path from source to sink
while self.BFS(source, sink, parent) :
# Find minimum residual capacity of the edges along the
# path filled by BFS. Or we can say find the maximum flow
# through the path found.
path_flow = float("Inf")
s = sink
while(s != source):
path_flow = min (path_flow, self.graph[parent[s]][s])
s = parent[s]
# Add path flow to overall flow
max_flow += path_flow
# update residual capacities of the edges and reverse edges
# along the path
v = sink
while(v != source):
u = parent[v]
self.graph[u][v] -= path_flow
self.graph[v][u] += path_flow
v = parent[v]
return max_flow
# Create a graph given in the above diagram
graph = [[0, 16, 13, 0, 0, 0],
[0, 0, 10, 12, 0, 0],
[0, 4, 0, 0, 14, 0],
[0, 0, 9, 0, 0, 20],
[0, 0, 0, 7, 0, 4],
[0, 0, 0, 0, 0, 0]]
g = Graph(graph)
source = 0; sink = 5
print ("The maximum possible flow is %d " % g.FordFulkerson(source, sink))此代码也是Edmonds-Karp算法,但与我实现的有所不同,不同在于,BFS函数在此代码里面,只是用来寻找增广路径,但最大流的计算还得在主函数里,通过parent这个list来回溯找到路径上的最小流的值。而本文实现的Edmonds-Karp算法,在BFS函数中,寻找增广路径的同时,也计算了路径的流的大小。所以本文实现的Edmonds-Karp算法的时间复杂度肯定比友情链接的Edmonds-Karp算法要小。
友情链接里面也说了,它的Edmonds-Karp算法的时间复杂度为 O(EV3) O ( E V 3 ) 。分析一下本文的时间复杂度,BFS函数的while循环最多V次数,主函数maxflow里面有两层while循环,第一层跟每次的增广路径的选择有关,最差的情况每次只选1的量,假设最大流是f,所以外层是f。内层循环也是最多V次数。所以本文的时间复杂度为 O(fV2) O ( f V 2 ) .
使用DFS的Ford-Fulkerson算法
既然有了用BFS的Ford-Fulkerson算法(即Edmonds-Karp算法),那我们再设计一个用DFS的Ford-Fulkerson算法。
递归设计错误示范
from queue import Queue
#n #边的个数
m = 6#点的个数
residual = [[0 for i in range(m)] for j in range(m)]
#残余图的剩余流量
maxflowgraph = [[0 for i in range(m)] for j in range(m)]
#记录最大流图,初始都为0
flow = [0 for i in range(m)]
#记录增广路径前进过程记录的最小流量
pre = [float('inf') for i in range(m)]
#记录增广路径每个节点的前驱,也记录该节点是否被路径记录
q = Queue()
#队列,用于BFS地寻找增广路径
#设置初始图的流量走向
residual[0][1]=3
residual[0][2]=2
residual[1][2]=1
residual[1][3]=3
residual[1][4]=4
residual[2][4]=2
residual[3][5]=2
residual[4][5]=3
def DFS(source,progress,sink):
print(progress,sink)
print(flow[progress])
print()
#source在有增广路径时,会一直前进到sink
if(progress == sink):
return flow[sink]
for i in range(m):
if( (i==progress) | (i==source) ):
continue
if( (residual[progress][i]>0) & (pre[i]==float('inf')) ):
pre[i] = progress
flow[i] = min(flow[progress],residual[progress][i])
return DFS(source,i,sink)
def maxflow(source,sink):
sumflow = 0#记录最大流,一直累加
augmentflow = 0#当前寻找到的增广路径的最小通过流量
flow[source] = float('inf')
while(True):
for i in range(m):
pre[i] = float('inf')
print('寻找增广路径')
augmentflow = DFS(source,source,sink)
#augmentflow = dfs(source,sink)
print('前驱数组为',pre)
print('最大流为',augmentflow)
if(augmentflow == -1):
break#返回-1说明已没有增广路径
k = sink
while(k!=source):#k回溯到起点,停止
prev = pre[k]#走的方向是从prev到k
maxflowgraph[prev][k] += augmentflow
residual[prev][k] -= augmentflow#前进方向消耗掉了
residual[k][prev] += augmentflow#反向边
k = prev
sumflow += augmentflow
return sumflow
result = maxflow(0,m-1)
print(result)
print(maxflowgraph)

截取了部分运行结果如上,报异常了程序终止:在第三次寻找增广路径时,由于程序走了一条错误的路径,导致在3,5的时候,即progress为3的时候,已经没有路径可以走了。但由于DFS递归函数是这么设计的:终点就return flow[sink]中间过程就是return DFS(source,i,sink)。这就导致递归函数无法回溯,路径到了死路无法原路返回一下再走下一个分支。这也导致了最大流为None,因为根据没有到达递归终点,但这个递归函数还非得返回一个值,所以只有返回一个None。
这也说明了,DFS函数的递归设计不应该这么设计,起码不应该有这种返回自身的函数语句return DFS(source,i,sink)。
递归正确设计
from queue import Queue
#n #边的个数
m = 6#点的个数
residual = [[0 for i in range(m)] for j in range(m)]
#残余图的剩余流量
maxflowgraph = [[0 for i in range(m)] for j in range(m)]
#记录最大流图,初始都为0
flow = [0 for i in range(m)]
#记录增广路径前进过程记录的最小流量
pre = [float('inf') for i in range(m)]
#记录增广路径每个节点的前驱,也记录该节点是否被路径记录
q = Queue()
#队列,用于BFS地寻找增广路径
#设置初始图的流量走向
residual[0][1]=3
residual[0][2]=2
residual[1][2]=1
residual[1][3]=3
residual[1][4]=4
residual[2][4]=2
residual[3][5]=2
residual[4][5]=3
def dfs(source,sink):
for i in range(m):
pre[i] = float('inf')
def real_dfs(source,progress,sink):
print(progress,sink)
if(progress == sink):
return
for i in range(m):
if( (i==progress) | (i==source) ):
continue
if( (residual[progress][i]>0) & (pre[i]==float('inf')) ):
pre[i] = progress
flow[i] = min(flow[progress],residual[progress][i])
real_dfs(source,i,sink)
real_dfs(source,source,sink)
if(pre[sink] != float('inf')):
return flow[sink]
else:
return -1
def maxflow(source,sink):
sumflow = 0#记录最大流,一直累加
augmentflow = 0#当前寻找到的增广路径的最小通过流量
flow[source] = float('inf')
while(True):
print('调用增广路径')
augmentflow = dfs(source,sink)
print('前驱数组为',pre)
print('最大流为',augmentflow)
if(augmentflow == -1):
break#返回-1说明已没有增广路径
k = sink
while(k!=source):#k回溯到起点,停止
prev = pre[k]#走的方向是从prev到k
maxflowgraph[prev][k] += augmentflow
residual[prev][k] -= augmentflow#前进方向消耗掉了
residual[k][prev] += augmentflow#反向边
k = prev
sumflow += augmentflow
return sumflow
result = maxflow(0,m-1)
print(result)
print(maxflowgraph)

运行结果如上,结果正确。这里的dfs函数只是一个壳子,外加每次初始化pre。real_dfs函数才是真正的递归函数,当progress == sink时,到达了递归终点,因为程序已经找到了增广路径。但观察运行结果发现,调用递归函数时,每次都会调用6次(即节点的个数),而且看前两次选择增广路径,明明都已经到达5 5,但程序还是向下执行了。
这是因为,如此设计的递归函数,会将所有递归分支都执行一遍,即使你以为你在终点progress == sink设置了return,但程序还是执行可执行的递归分支。(想象一棵递归树,会执行到所有的叶子节点)。
递归次数优化
修改dfs函数如下:
def dfs(source,sink):
for i in range(m):
pre[i] = float('inf')
flag = False
def real_dfs(source,progress,sink):
nonlocal flag
if(flag == True):
return#此时程序已经找到增广路径,之后的递归分支不需要执行
print(progress,sink)
if(progress == sink):
flag = True
return
for i in range(m):
if( (i==progress) | (i==source) ):
continue
if( (residual[progress][i]>0) & (pre[i]==float('inf')) ):
pre[i] = progress
flow[i] = min(flow[progress],residual[progress][i])
real_dfs(source,i,sink)
real_dfs(source,source,sink)
if(pre[sink] != float('inf')):
return flow[sink]
else:
return -1设置一个外部变量flag,一旦路径到达了sink点,便置反flag。并且在递归函数里判断这个flag。运行结果如下:

可见,每次寻找增广路径时,只要递归到达5 5,之后的递归分支便每次直接return。
最大流图的最后抵消

运行结果的最大流图如下:

它与最终的最大流图,还差在,正反向边还没有互相抵消掉。所以在打印最大流图前,添加如下代码即可。
for i in range(m):
for j in range(m):
if( (maxflowgraph[i][j]!=0)&(maxflowgraph[j][i]!=0)):
#如果程序结束后,最大流图还有正反向边没有互相抵消
temp = min(maxflowgraph[i][j],maxflowgraph[j][i])
maxflowgraph[i][j] -= temp
maxflowgraph[j][i] -= tempDinic算法
geeksforgeeks的友情链接Dinic’s algorithm for Maximum Flow。虽然用英文写的,但是特别好懂,大家可以去看一下,我就是看这个看懂的。总的来说,Dinic’s算法是将BFS和DFS相结合的算法。
In Edmond’s Karp algorithm, we use BFS to find an augmenting path and send flow across this path. In Dinic’s algorithm, we use BFS to check if more flow is possible and to construct level graph. In level graph, we assign levels to all nodes, level of a node is shortest distance (in terms of number of edges) of the node from source. Once level graph is constructed, we send multiple flows using this level graph. This is the reason it works better than Edmond Karp. In Edmond Karp, we send only flow that is send across the path found by BFS.
Dinic’s算法与Edmond-Karp算法的区别在于。在Edmond-Karp算法中,我们用BFS找到增广路径并且通过该路径发送流。在Dinic’s算法中,我们用BFS检测是否有更多可能的增广路径,为此我们要构造层次图。在层次图中,给每个节点标记一个数,这个数是从源点到该点的无权最短路径(shortest distance in terms of number of edges)。一旦层次图构造好了,我们便通过层次图来发送多个流。这就是为什么此算法优于Edmond-Karp算法的原因。因为Edmond-Karp算法只会每次通过BFS找到一条增广路径,再发送路径上的这条流。
通过层次图来寻找增广路径,每条增广路径上的节点的层次依次为0,1,2,3…。如果从层次图中,已经找不到这样的路径,说明该层次图的可行的增广路径已经找完了。
基本思想
原图以及残余图如下:

第一次迭代:

使用无权最短路径的思想(把每条边的权值都看成1),为每个点标注层次,比如s点的层次为0;12点的层次为1;34点的层次为2;t点的层次为3.
然后我们在层次图,寻找层次逐渐变大(层次依次为0,1,2,3…)的增广路径,一旦找到一条路径,便对残余图作相应的修改,直到不能找到这样的路径为止。
一共能找到3条路径:
4 units of flow on path s – 1 – 3 – t.
6 units of flow on path s – 1 – 4 – t.
4 units of flow on path s – 2 – 4 – t.
Total flow = Total flow + 4 + 6 + 4 = 14
第一次迭代之后:

第二次迭代:

一共找到一条路径:
5 units of flow on path s – 2 – 4 – 3 – t
Total flow = Total flow + 5 = 19
第二次迭代之后:

第三次迭代:
这时我们发现,再也找不到层次逐渐变大(层次依次为0,1,2,3…)的增广路径了,所以算法终止。
设计程序
大概会有三个函数:
第一个是建立层次图的函数,每次为每个节点标上层次号。此函数是用BFS的思路来做,过程类似无权最短路径。
第二个是根据层次图找到所有的层次逐渐变大(层次依次为0,1,2,3…)的增广路径。此函数是利用DFS的思路来做,深度递归到sink时,说明找到了一条增广路径。
第三个是根据增广路径,对残余图和最大流图作出相应的修改。
大体思路是这样,但实际编程中有所出入,但理解这个思路,是很重要的。
从上面可以看出来,Dinic’s算法是将BFS和DFS相结合的算法。
代码实现
使用的图,以及其最大流图如下:

按照以上设计程序的思路,用python3实现了如下代码:
from queue import Queue
#n #边的个数
m = 6#点的个数
residual = [[0 for i in range(m)] for j in range(m)]
#残余图的剩余流量
maxflowgraph = [[0 for i in range(m)] for j in range(m)]
#记录最大流图,初始都为0
flow = [0 for i in range(m)]
#记录增广路径前进过程记录的最小流量
pre = [float('inf') for i in range(m)]
#记录增广路径每个节点的前驱,也记录该节点是否被路径记录
level = [float('inf') for i in range(m)]
#代表层次图,层次从0开始
sumflow = 0
#设置初始图的流量走向
residual[0][1]=10
residual[0][2]=10
residual[1][2]=2
residual[1][3]=4
residual[1][4]=8
residual[2][4]=9
residual[4][3]=6
residual[3][5]=10
residual[4][5]=10
def build_level(source,sink):
#根据残余图来构建层次图,过程类似无权最短路径
level[source] = 0#源点的层次为0
level_pre = [float('inf') for i in range(m)]
#构造层次图用到的前驱表,用来标记该节点已标记为层次
q = Queue()
#队列,用于BFS地寻找增广路径
q.put(source)
while(not q.empty()):
current = q.get()
for i in range(m):
if( (i==source) | (i==current) ):
continue#源点和自身不用分析
if((residual[current][i]>0)&(level_pre[i]==float('inf'))):
#只要能往下走且没有被标记过
level_pre[i] = current
#标记前驱,也代表已构造了层次
level[i] = level[current]+1
#层次逐渐加1
q.put(i)
#加入队列
print('层次图为',level)
if(level_pre[sink]!=float('inf')):
#如果构造层次图能构造到sink点,说明有增广路径
return True
else:
return False
def get_augment(source,sink):
#根据层次图,构造可能的增广路径
temp_augment = [source]
#每条增广路径都是从源点开始的
count = 1#源点下一层的层次为1
def recursion(count):
for i in range(m):
if(level[i]==count):#寻找层次为count的点
temp_augment.append(i)
if(i == sink):
#i到了sink,说明找到了一条可能的增广路径
print('可能的增广路径',temp_augment)
#可能的增广路径是层次图的排列组合而来
send_flow(temp_augment,source,sink)
recursion(count+1)#寻找下一层次的点
temp_augment.remove(i)
#删除掉i,为下一次递归作准备
recursion(count)
print()
def send_flow(augment,source,sink):
#根据可能的增广路径,判断其是否为一条可行的增广路径
global sumflow
flow[sink] = float('inf')#设为无穷,且以这个作为找到增广路径的标志
print('初始flow',flow)
for i in range(len(augment)-1):
flow[augment[i+1]] = min(flow[augment[i]],residual[augment[i]][augment[i+1]])
print('行进增广路径过程中的flow',flow)
if(flow[sink] != 0):
#flow[sink]不为0,说明增广路径有效
sumflow += flow[sink]
print('有效的增广路径',augment,flow)
for i in range(len(augment)-1):
#对残余图和最大流图的相应修改
residual[augment[i]][augment[i+1]] -= flow[sink]
residual[augment[i+1]][augment[i]] += flow[sink]
maxflowgraph[augment[i]][augment[i+1]] += flow[sink]
print()
def dinic(source,sink):
flow[source] = float('inf')
#源点的flow为无穷,方便以后取较小数,且源点的flow永远为无穷
while(True):
temp = build_level(source,sink)
if(temp is False):
break
else:
get_augment(source,sink)
dinic(0,m-1)
print(sumflow)
print(maxflowgraph)代码的具体细节请看注释。运行结果如下:

主函数dinic一直调用build_level函数,来查看是否能在当前残余图上建立层次图,如果不能,说明最大流已经找完了,便结束循环。
build_level函数,根据当前残余图建立残余图,过程类似于无权最短路径(BFS),利用队列和前驱数组level_pre来实现,如果能建立层次图,返回真,否则返回假。

get_augment函数,根据当前层次图获得一条可能的增广路径(为什么是说可能呢,因为这是通过层次从低到高排列组合而来的,比如通过第一次层次图会发现四条可能的增广路径:[0, 1, 3, 5],[0, 1, 4, 5],[0, 2, 3, 5], [0, 2, 4, 5]。看上图可以发现只有4条可能的路径。但实际上有效的只有,[0, 1, 3, 5],[0, 1, 4, 5], [0, 2, 4, 5])。寻找增广路径的方法是通过DFS即深度遍历,一旦发现一条增广路径,便将路径传给send_flow函数。
send_flow函数,根据传来的增广路径和当前的残余图,如果通过传来的路径能流过不为0的流(如果路径不有效,那么走完路径,流的量为0),那么判断此增广路径有效,再对残余图以及最大流图作相应的修改
此代码实现,结构层次清晰,方便编程实现。
另一种代码实现
由于本人的奇思妙想,我就想,能不能编写这么多函数。最好只用一个函数:首先可以不需要层次图,只需要按照层次来前进选择增广路径;选择增广路径还是按照DFS的思想(肯定得用到递归);每当找到一条可行的增广路径便对残余图作修改。
代码如下:
#n #边的个数
m = 6#点的个数
residual = [[0 for i in range(m)] for j in range(m)]
#残余图的剩余流量
maxflowgraph = [[0 for i in range(m)] for j in range(m)]
#记录最大流图,初始都为0
flow = [0 for i in range(m)]
#记录增广路径前进过程记录的最小流量
pre = [float('inf') for i in range(m)]
#记录增广路径每个节点的前驱,也记录该节点是否被路径记录
sumflow = 0
#记录最大流
#设置初始图的流量走向
residual[0][1]=10
residual[0][2]=10
residual[1][2]=2
residual[1][3]=4
residual[1][4]=8
residual[2][4]=9
residual[4][3]=6
residual[3][5]=10
residual[4][5]=10
def label_next_level(source,progress):
#标记progress节点的下一层次的节点对应的pre
#并且label数组保存标记的节点
label = []
for i in range(m):
if( (i==progress) | (i==source) ):
continue
if( (residual[progress][i]>0) & (pre[i]==float('inf')) ):
label.append(i)
pre[i] = progress
return label
def nonlabel_next_level(label):
#为下一次递归分支作准备时,调用此函数
#将label_next_level函数标记过的节点
#再标记回无穷
for i in label:
pre[i] = float('inf')
def solve(source,sink):
print('新的一次调用')
#虽然感觉需要保存层次图信息,但实际只要无权最短路径进行就行
#所以此程序没有数据结构保存层次图,但下面的bfs函数是按照层次图
#层次大小顺序进行递归的
for i in range(m):
pre[i] = float('inf')
#初始化pre数组
level_path = [source]
#此list保存递归中找到的增广路径,必有source
flag = False
#此标志位就来表示此次调用solve函数是否有找到增广路径
def bfs(progress,sink):
label = []#保存在pre里标记过的节点
nonlocal level_path,flag
global sumflow
if(progress == sink):#递归终点,但这么说不准确,因为之后递归还在执行
#因为可能还有增广路径,所以得执行完所有递归分支
#每当到了这个分支,就说明找到了一条增广路径
flag = True
#置反flag
sumflow += flow[sink]
#最大流的量
for i in range(len(level_path)-1):
#对最大流图和残余图做相应的操作
residual[level_path[i]][level_path[i+1]] -= flow[sink]
residual[level_path[i+1]][level_path[i]] += flow[sink]
maxflowgraph[level_path[i]][level_path[i+1]] += flow[sink]
#根据层次路径,更新flow,为下一次作准备
#这里是提前计算好flow,本来flow是每次找增广路径时,从头开始算,而且不用提前
#但由于第二次找增广路径时,是从递归的某次分支找到的,但分支的这个节点的flow
#还没有按照从源点更新flow那么更新好
for i in range(len(level_path)-1):
if(residual[level_path[i]][level_path[i+1]] > 0):
flow[level_path[i+1]] = min(residual[level_path[i]][level_path[i+1]],flow[level_path[i]])
else:
#如果小于等于0了,说明第二次增广路径也肯定不会从这个分支分支了
break
print(level_path)
print(flow[sink])
for i in range(m):
if( (i==progress) | (i==source) ):
#前进过程不能回到源点source
#前进过程也不能回到自身progress
continue
if( (residual[progress][i]>0) & (pre[i]==float('inf')) ):
#从progress到i有正向边,且i没有被标记过
level_path.append(i)
label = label_next_level(source,progress)
#标注progress下一层次的节点
flow[i] = min(flow[progress],residual[progress][i])
print(progress,i,'before',pre)
bfs(i,sink)
level_path.remove(i)
nonlabel_next_level(label)
print(progress,i,'after',pre)
bfs(source,sink)
return flag
def dinic(source,sink):
flow[source] = float('inf')
#源点的flow为无穷,方便以后取较小数,且源点的flow永远为无穷
while(True):
temp = solve(source,sink)
#solve函数每次进行层次图的遍历
#solve函数每次有可能根据层次图找出多个增广路径
if(temp is False):
break
return sumflow
result = dinic(0,m-1)
print()
print(result)
print(maxflowgraph)代码的具体细节请看注释。运行结果如下:
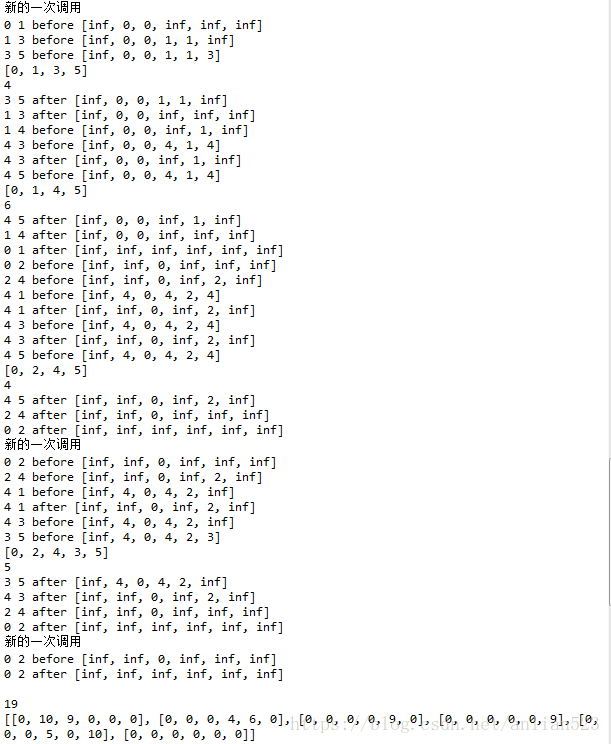
此代码的精华在于,使用层次图的思想,每当递归到第i层,就把第i层的节点都给标记成已走过(标记pre数组,通过调用label_next_level函数),这样,在寻找增广路径的下一个节点时,肯定只能寻找到i+1层的节点,这样就不需要层次图就实现了层次图的功能。并且当此层递归结束前,将label_next_level函数标记过的节点,再标记回初始状态(通过label数组记录,并且将label传给nonlabel_next_level函数)。
运行结果中的before和after,代表进入到下一层递归之前和之后。这里需要注意得是运行结果中的0 2 before [inf, inf, 0, inf, inf, inf],运行到这里,之前已经找到了[0, 1, 3, 5] [0, 1, 4, 5]这两条增广路径,可以看出,在深度递归,0到1里面的增广路径已经找完,这时递归回到0到2,但运行结果里0 2 before [inf, inf, 0, inf, inf, inf]却没有把前驱数组的里面的1索引标记(按照上一段的思想,进入到了第1层,就应该把1索引和2索引都标记了,因为12索引是层次图中的第1层,应该是要把这一层都标记),但实际上,这里不需要标记1索引,因为递归内部是循环来分的分支,而0到1这个分支已经执行过了,所以就算这里1索引没有标记,也不会走0到1这个分支了。
总结就是,此代码费了好多脑细胞,如果已经有了好思路,还是按照好思路编程吧。你们要是理解了正常的代码实现,理解这另一种代码实现应该也不难。此代码实现的代码量比上一种的少,时间复杂度上来说也比上一种小。