数据挖掘之_SVD的python实现和分析pin
前言
今日实现第一个推荐算法,在”机器学习实战“一书中找到了SVD方法一章练习。这里总结下笔记经验,与大家分享 。
简介
对于一个简单的推荐系统,例如电影推荐,我们知道N个用户对M个电影的评分。这时候对于一个新的用户,我们应该如何给他推荐新的电影呢?一个最简单的方法,根据用户已看的电影,找出与他相似的用户,然后推荐其他未看的高得分的电影。SVD提供了一个更加准确的解决方案。其基本思想是,降维!
对于电影,一般的推荐算法是将每个电影的评分作为一个维度,对于Xi用户,就有一个矩阵行 Xi = [xi1,xi2,xi3....xij]。 但是电影如此之多,每个人又不可能看过所有的电影,这将造成矩阵非常巨大,然后非常稀疏。SVD的具体思想是提取电影的参数Q1, ..., Qj。这个参数可以表达为电影的动作,搞笑,恐怖等程度的描述。因此后面的推荐算法中,我们不需要对每个电影的口味进行分析,当给定新用户的时候直接推荐适合他口味,即基于电影参数Qj的一个评分相符,的电影即可。
实现
实现SVD,只需要python中的numpy,其中有一个线性代数工具箱linalg。
import numpy as np
data = [[1,2,3],[2,2,3],[3,3,3]]
U,S,V = np.linalg.svd(data)
>>> U
array([[-0.48273945, 0.76567677, 0.42509024],
[-0.54696309, 0.11548497, -0.82915294],
[-0.68395468, -0.63277351, 0.36304778]])
>>> S
array([ 7.51653849, 1.17761678, 0.33892171])
>>> V
array([[-0.48273945, -0.54696309, -0.68395468],
[-0.76567677, -0.11548497, 0.63277351],
[-0.42509024, 0.82915294, -0.36304778]])
看到这里是否想起了PCA分析,同样的分解矩阵,同样的计算能量信息。下面讨论章节我会进行一些个人总结。
那么算法实现了,具体应用到推荐中该如何做呢?对于用户没有看过的电影,我们只需要计算与用户看过的电影中的高评分电影的相似度,然后推荐相似度高的电影即可。你或许听过协同过滤(collaborative filtering),没听过没关系,我们要做得就是协同过滤。也就是基于用户与其他用户的数据进行对比来实现精确推荐。另外还有可以基于内容的推荐,不在本文考虑范围。
计算相似度的集中方法,有:
欧式距离,数据差的的平方和
相关系数,一般为皮尔逊相关系数(Pearson correlation)
余弦相似性,两个向量的余弦夹角的大小
注意,计算相似度后,最好把数据归一化,一般归一化到0-1的范围。计算相似度中我们一般考虑使用基于物品的相似度的分析。原因是由实际考虑的。设想你有一个商店,商品种类可能不太会变动,但是用户不断进进出出,那么计算那个方便呢! 对,由于物品的稳定性更高,计算量小,那么就基于物品的推荐即可。
事例
假设你有一家餐馆,然后有数据(自己想想数据是什么吧)。怎么给用户推荐他没有尝试过的菜品呢。一般我们看到是直接上我们的特色菜,这个就没有针对性了。我们试试基于SVD的推荐算法。具体步骤为:
(1)收集数据!
(2)建立用户评价矩阵
(3)针对特定用户,找到其没有评价的物品,计算其评分
(4)将预测的物品评分从大到小排序,然后推荐给用户。
结合最后的程序,运行下面的推荐命令,即可完成给用户0推荐3个产品的任务
user = 0
dataMat = mat(loadExData2())
# 直接实现
rec1 = recommend(dataMat, user, N=3, simMeas=cosSim, estMethod=standEst)
# 采用SVD方法实现
rec2 = recommend(dataMat, user, N=3, simMeas=cosSim, estMethod=svdEst)(Pdb) rec1
[(0, 5.0), (1, 5.0), (2, 5.0)]
(Pdb) rec2
[(7, 4.5148349067003304), (8, 4.514365463123859), (0, 4.5142831096323039)]讨论
(1)SVD全程为Singular Value Decomposition, 即奇异值分解。假设原始数据为m*n的矩阵,SVD会将矩阵分解为三个矩阵的乘积,中间的矩阵为一个对角不为零其余元素为0的矩阵。那些部位0的对角元素即为奇异值。
(2)SVD其实是一种矩阵分解技术,不同的矩阵分解技术可能适合不同的应用。其他技术,例如PCA。同样可以用于图像压缩等其他应用。
(3)其他推荐算法。
试想另外一种情形,假设一个商家想看怎么捆绑销售可以获得利益最大化怎么办。这时候要考虑在所有销售商品中,哪两种或几种商品销售趋势很一致。这其实也是一种推荐过程。这个过程中用户的评价暂时忽略,我们尝试找销售量相似的产品。这里提供一下大致的思路。
a, 计算两两产品的相关系数
b, 对某一产品,按照相关系数排序
c, 对排序结果,挑选相关系数最大的物品做捆绑销售。
(4)SVD算法其实会消耗大量的网络资源。因此实际操作的时候考虑到效率问题,大规模计算一般会是在离线情况下一天计算一次相似性,并且保存相似性得分。加入网站刚开始建立,数据量不足(冷启动问题),可以考虑用搜索问题来解决推荐。
理论上有很多推荐的算法,按内容推荐, 协同过滤(包括item-based, user-based, SVD分解等),上下文推荐,Constraint-based推荐,图关系挖掘等。很多比较牛的单个算法, 就能在某个指标上取得较好效果, 例如MAE,RMSE。。。不过有自己的优点, 每种算法也有自己的缺点, 例如按内容推荐主要推荐和用户历史结果相似的item,一般的item-based容易推荐热门item(被更多人投票过)。。。。 所以在工业界,例如各互联网公司, 都会使用多种算法进行互相配合, 取长补短, 配合产品提升效果。而且在完整的推荐系统中,不仅有传统的Rating推荐, 还需要辅以非常多的挖掘, Ranking来达到预期效果。
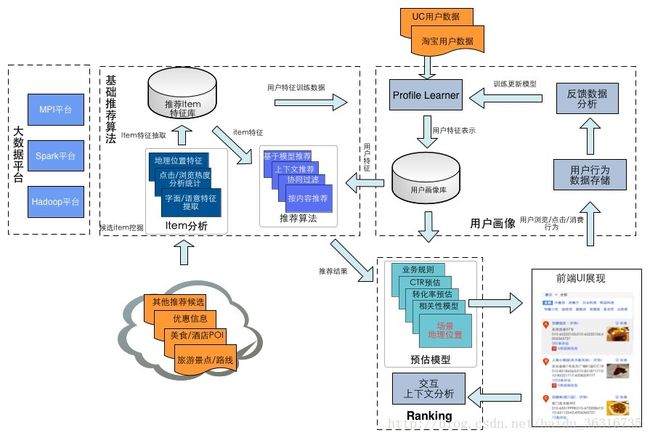
图片来自引用参考2
#!/usr/bin/env python
# -*- coding: UTF-8
from numpy import *
from numpy import linalg as la
import numpy as np
def loadExData2():
return[[0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 5],
[0, 0, 0, 3, 0, 4, 0, 0, 0, 0, 3],
[0, 0, 0, 0, 4, 0, 0, 1, 0, 4, 0],
[3, 3, 4, 0, 0, 0, 0, 2, 2, 0, 0],
[5, 4, 5, 0, 0, 0, 0, 5, 5, 0, 0],
[0, 0, 0, 0, 5, 0, 1, 0, 0, 5, 0],
[4, 3, 4, 0, 0, 0, 0, 5, 5, 0, 1],
[0, 0, 0, 4, 0, 4, 0, 0, 0, 0, 4],
[0, 0, 0, 2, 0, 2, 5, 0, 0, 1, 2],
[0, 0, 0, 0, 5, 0, 0, 0, 0, 4, 0],
[1, 0, 0, 0, 0, 0, 0, 1, 2, 0, 0]]
def ecludSim(inA,inB):
return 1.0/(1.0 + la.norm(inA - inB))
def pearsSim(inA,inB):
if len(inA) < 3 : return 1.0
return 0.5+0.5*corrcoef(inA, inB, rowvar = 0)[0][1]
def cosSim(inA,inB):
num = float(inA.T*inB)
denom = la.norm(inA)*la.norm(inB)
return 0.5+0.5*(num/denom)
def standEst(dataMat, user, simMeas, item):
'''
计算相似性
数据矩阵,用户ID, 相似度方法, 物品ID
simMeas: ecludSim, pearsSim, cosSim
'''
n = shape(dataMat)[1]
simTotal = 0.0; ratSimTotal = 0.0
# 不同的物品
for j in range(n):
userRating = dataMat[user,j]
if userRating == 0: continue
# 对两个物品,item和j,考虑都有评价的部分
overLap = nonzero(logical_and(dataMat[:,item].A>0, \
dataMat[:,j].A>0))[0]
if len(overLap) == 0:
similarity = 0
else:
similarity = simMeas(dataMat[overLap,item], \
dataMat[overLap,j])
print 'the %d and %d similarity is: %f' % (item, j, similarity)
simTotal += similarity
ratSimTotal += similarity * userRating
# 返回归一化的结果
if simTotal == 0:
return 0
else:
return ratSimTotal/simTotal
def svdEst(dataMat, user, simMeas, item):
'''
基于SVD的相似性计算
'''
n = shape(dataMat)[1]
simTotal = 0.0; ratSimTotal = 0.0
U,Sigma,VT = la.svd(dataMat)
# 只考虑前四个元素,转化成矩阵形式
Sig4 = mat(eye(4)*Sigma[:4]) #arrange Sig4 into a diagonal matrix
# 将数据降维转化
xformedItems = dataMat.T * U[:,:4] * Sig4.I #create transformed items
for j in range(n):
userRating = dataMat[user,j]
if userRating == 0 or j==item: continue
similarity = simMeas(xformedItems[item,:].T,\
xformedItems[j,:].T)
print 'the %d and %d similarity is: %f' % (item, j, similarity)
simTotal += similarity
ratSimTotal += similarity * userRating
if simTotal == 0: return 0
else: return ratSimTotal/simTotal
def recommend(dataMat, user, N=3, simMeas=cosSim, estMethod=standEst):
'''
针对某一用户,user,进行推荐。返回dictionary
N : 推荐物品个数
simMeas : 相似性计算方法
estMethod : 针对某一用户的某一物品,计算相似性的程序,返回向量。
'''
unratedItems = nonzero(dataMat[user,:].A==0)[1]#find unrated items
if len(unratedItems) == 0: return 'you rated everything'
itemScores = []
for item in unratedItems:
estimatedScore = estMethod(dataMat, user, simMeas, item)
itemScores.append((item, estimatedScore))
return sorted(itemScores, key=lambda jj: jj[1], reverse=True)[:N]
def printMat(inMat, thresh=0.8):
for i in range(32):
for k in range(32):
if float(inMat[i,k]) > thresh:
print 1,
else: print 0,
print ''
def imgCompress(numSV=3, thresh=0.8):
# 用svd方法进行图像压缩
myl = []
for line in open('0_5.txt').readlines():
newRow = []
for i in range(32):
newRow.append(int(line[i]))
myl.append(newRow)
myMat = mat(myl)
print "****original matrix******"
printMat(myMat, thresh)
U,Sigma,VT = la.svd(myMat) # svd
SigRecon = mat(zeros((numSV, numSV)))
for k in range(numSV):#construct diagonal matrix from vector
SigRecon[k,k] = Sigma[k]
# reconstruct with the first numSV feature
reconMat = U[:,:numSV]*SigRecon*VT[:numSV,:]
print "****reconstructed matrix using %d singular values******" % numSV
printMat(reconMat, thresh)
参考
机器学习实战
一个完整推荐系统实现